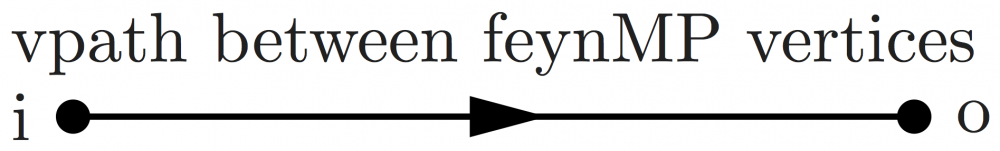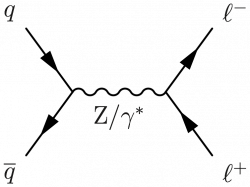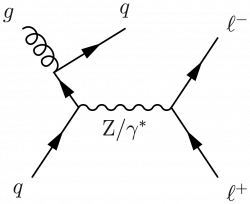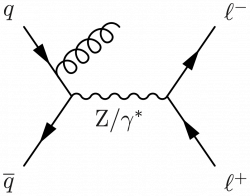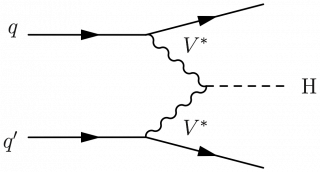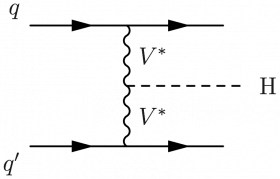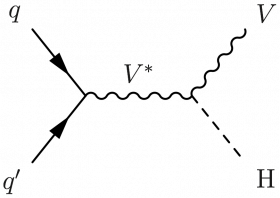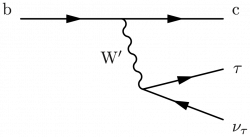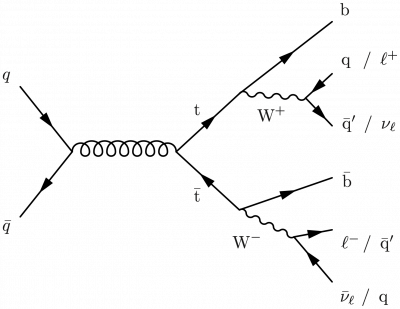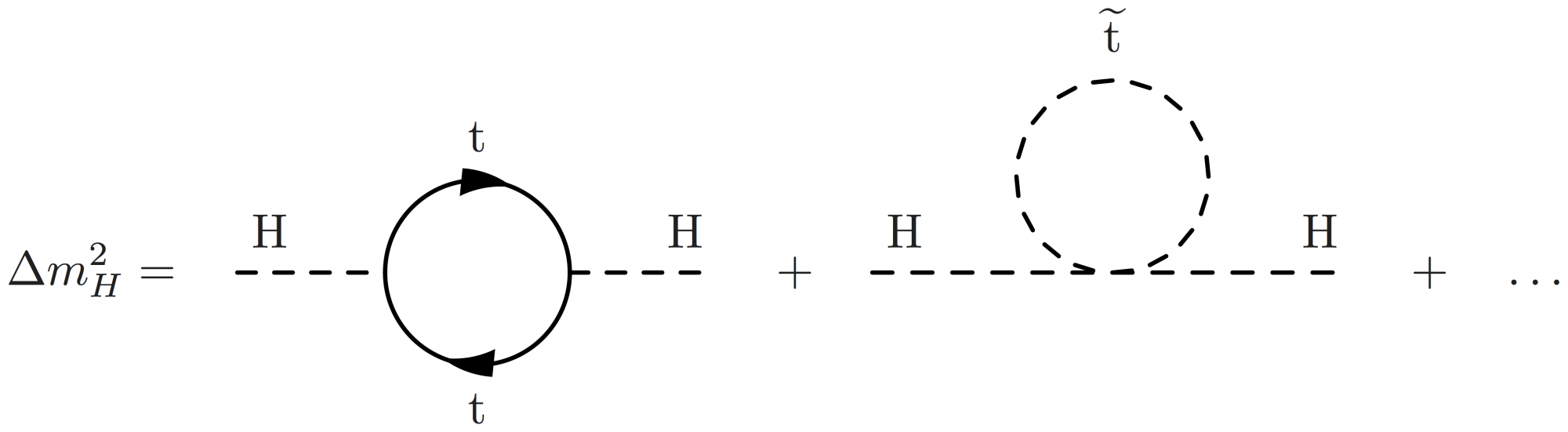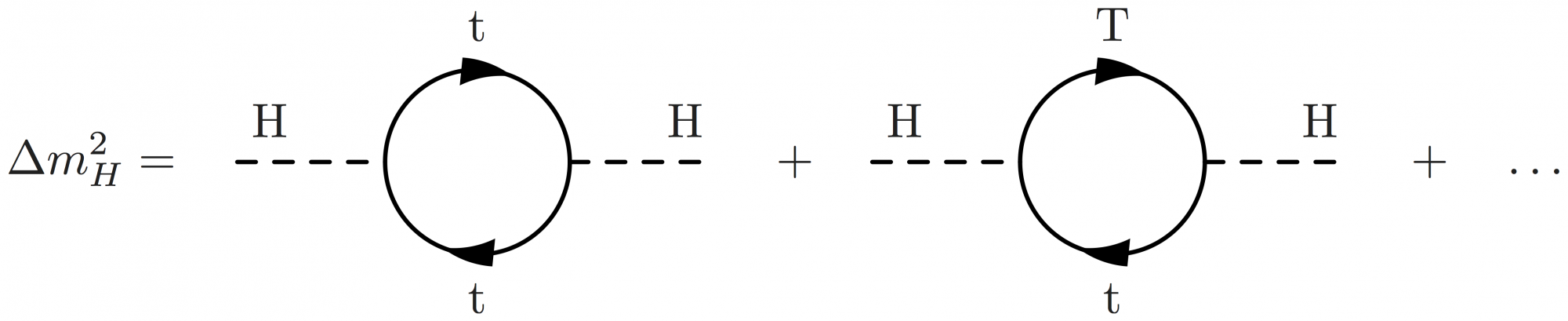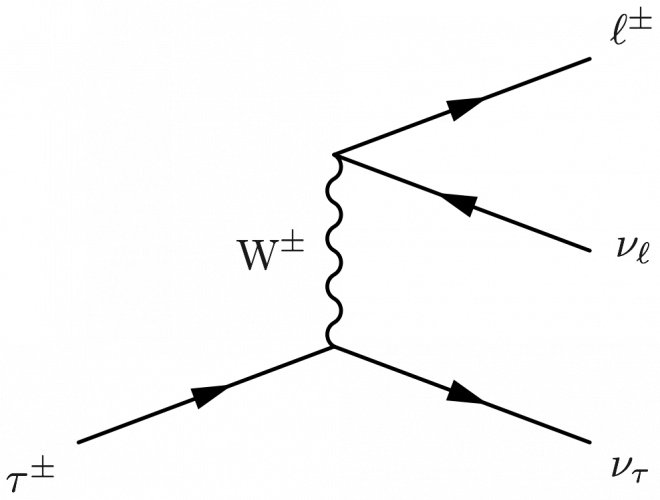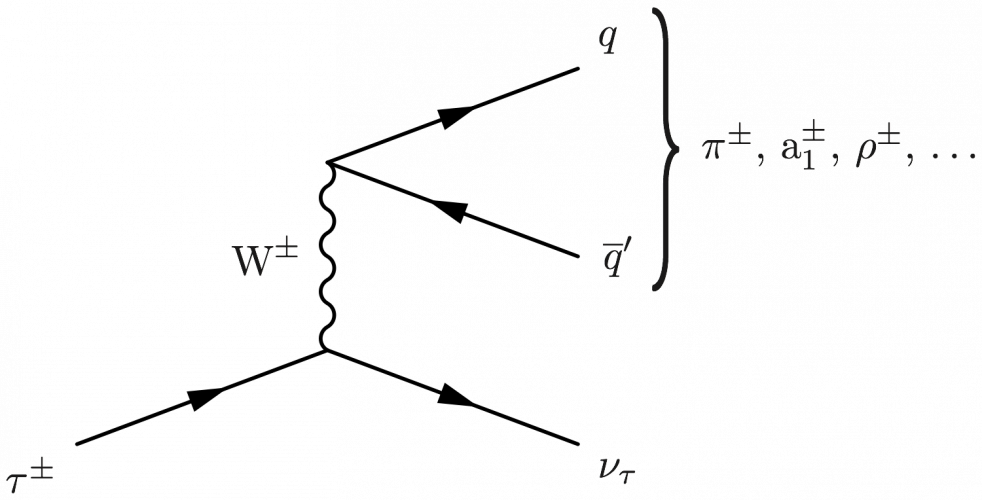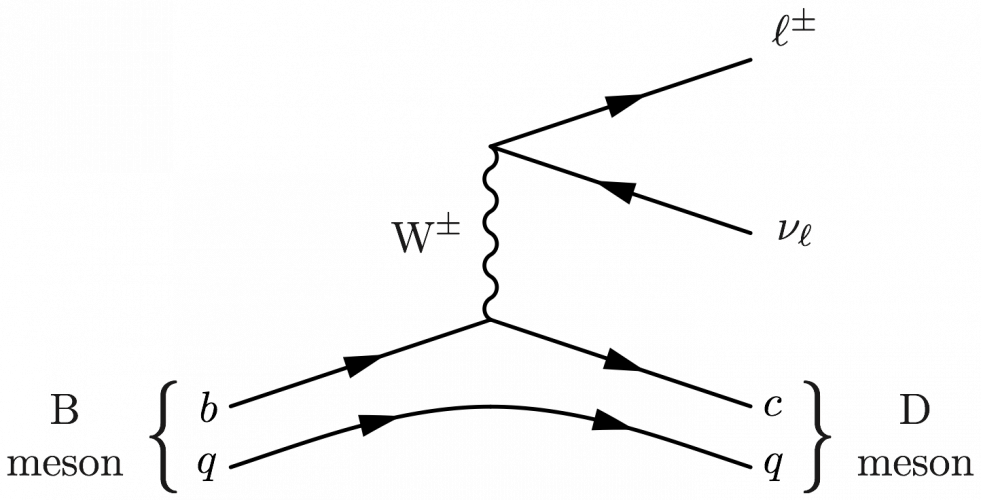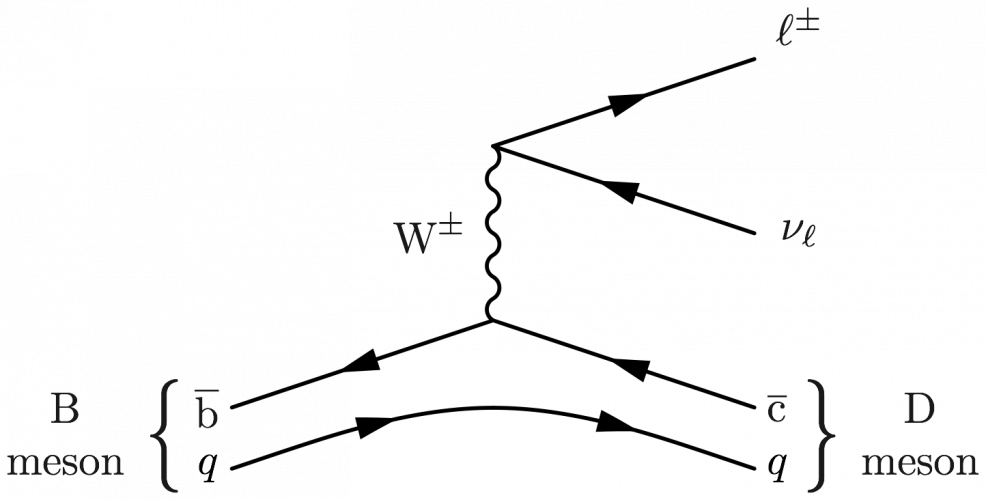Table of Contents
How to make Feynman diagrams in LaTeX
This page shows some of the basics of making Feynman diagrams in LaTeX with the feynMF/feynMP package. You will also find many examples relevant for our group. More information can be found at:
- for advanced stuff with
MetaPost, check out the MetaPost manual (J.D. Hobby, 2017), this paper, this tutorial and this section; - ready-made SUSY diagrams (images), with the code (GitHub);
- how to set up feynMP in LaTeXiT on Mac OS X to make Feynman diagrams as standalone images (strongly recommended);
Simple example: electron - muon scattering
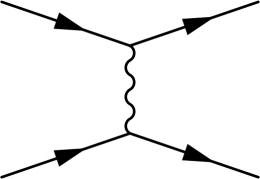
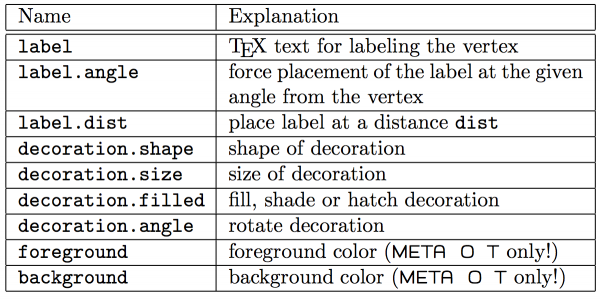
The most basic example is electron - muon scattering with a photon propagator. Use \fmfleft for creating and labeling the external vertices of incoming legs and \fmfright for outgoing ones. Connect the electron line to the vertices and create internal ones with \fmf{fermion}. Then connect a photon \fmf{photon} to the internal vertices.
\begin{fmffile}{feyngraph} \begin{fmfgraph}(110,60) \fmfleft{i1,i2} \fmfright{o1,o2} \fmf{fermion}{i1,v1,o1} \fmf{fermion}{i2,v2,o2} \fmf{photon}{v1,v2} \end{fmfgraph} \end{fmffile}
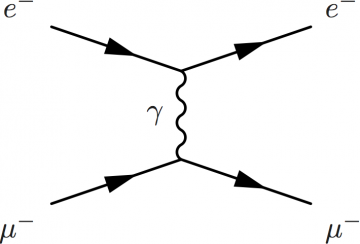
Use the label option of \fmf to name a leg and the command \fmflabel (or \fmfv) to label vertices.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i1,i2} \fmfright{o1,o2} \fmflabel{$\mu^-$}{i1} \fmflabel{$e^-$}{i2} \fmflabel{$\mu^-$}{o1} \fmflabel{$e^-$}{o2} \fmf{fermion}{i1,v1,o1} \fmf{fermion}{i2,v2,o2} \fmf{photon,label=$\gamma$}{v1,v2} \end{fmfgraph*} \end{fmffile}
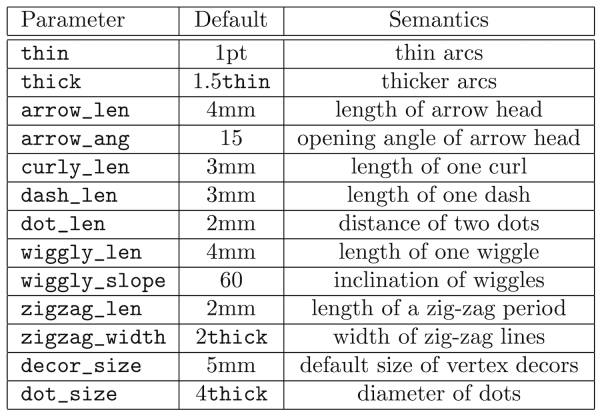
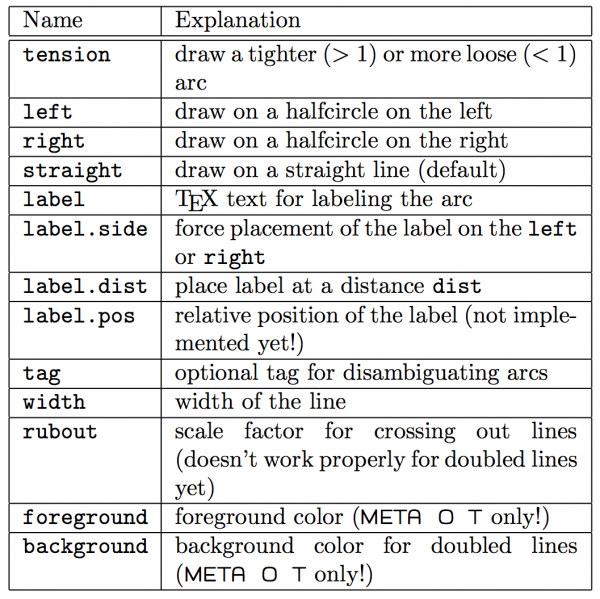
Checkout the feynMF manual for all the available line styles, line options, vertex options and all their parameters.
(Tables from the manual.)
To put a dot on a vertex, you can use these two equivalent options:
\fmfdot{v} \fmfv{decor.shape=circle,decor.filled=full,decor.size=4}{v} \fmfv{decor.shape=circle,decor.filled=full,decor.size=2thick}{v}
To make blobs for generic, effective field theory or beyond the standard model processes:
\fmfblob{10}{v} \fmfv{decor.shape=circle,decor.filled=shaded,decor.size=10}{v}
Emphasizing legs with color and width
To emphasize some legs, use the option foreground where you can set the color with a normalized decimal RBG value separated by two commas foreground=(<red>,,<blue>,,<green>). You can easily find websites like this one to get the RBG color code from some image, or with a color wheel this one, or you can use the DigitalColor Meter application of Max OS X (in Applications/Utilities).
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i1,i2} \fmfright{o1,o2} \fmf{fermion,foreground=(1,,0.1,,0.1)}{i1,v1,o1} \fmf{fermion}{i2,v2,o2} \fmf{photon}{v1,v2} \end{fmfgraph*} \end{fmffile}
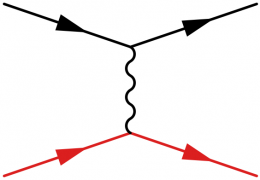
Furthermore you can emphasize some leg with the width option of \fmf, or use \fmfpen{thick} to make the whole diagram thick (default setting is thin).
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i1,i2} \fmfright{o1,o2} \fmf{fermion,width=2}{i1,v1,o1} \fmf{fermion}{i2,v2,o2} \fmf{photon}{v1,v2} \end{fmfgraph*} \end{fmffile}
Shaping diagrams with tension, freezing and phantom lines
Tension
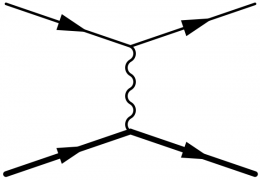
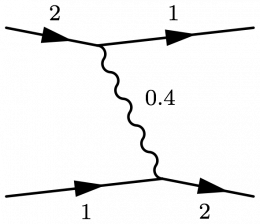
You can control a leg's length and its pull on vertices and other legs by changing \fmf's tension option from the default value of 1.
\begin{fmffile}{feyngraph} \begin{fmfgraph}(110,60) \fmfleft{i1,i2} \fmfright{o1,o2} \fmf{fermion}{i1,v1} \fmf{fermion,tension=2}{v1,o1} % make shorter \fmf{fermion,tension=2}{i2,v2} % make shorter \fmf{fermion}{v2,o2} \fmf{photon,tension=0.4}{v1,v2} % make longer \end{fmfgraph} \end{fmffile}
Using \fmffreeze and drawing invisible lines with \fmf{phantom} can also help to control the shape. By drawing a phantom line with some well-chosen tension, you can “pull” vertices in other directions. By freezing after drawing part of your diagram, you prevent these new lines from pulling it out of the desired shape.
Vertex positioning and distribution
As documented in the feynMF manual, the external vertices are by default (or explicitly with \fmfcurved) positioned on a curve:
Left to right: \fmfbottom, \fmfleft, \fmfsurround, \fmftop and \fmfright.
If you prefer the external vertices aligned on a straight box, use \fmfstraight:
(Images from the manual.)
Phantoms, freezing and tension
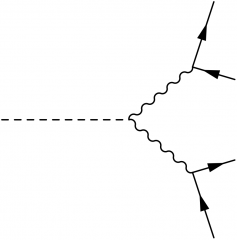
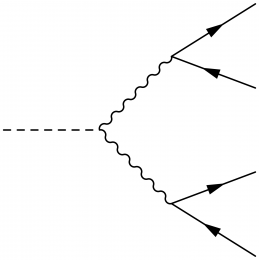
How can you have more control over the line length and vertex positions? Consider making a diagram of a Higgs boson decaying into two W bosons (H → WW → 4f) without the use of tension:
\begin{fmffile}{feyngraph} \begin{fmfgraph}(150,150) \fmfleft{i1} \fmfright{o1,o2,o3,o4} \fmf{dashes}{i1,v1} \fmf{boson}{v1,v21} \fmf{boson}{v1,v22} \fmf{fermion}{o1,v21,o2} \fmf{fermion}{o3,v22,o4} \end{fmfgraph} \end{fmffile}
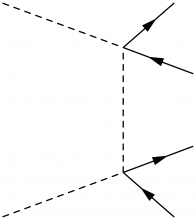
This was pretty straightforward, but perhaps you prefer the fermion lines to be equal in length. This can be achieved by drawing help lines, which pull back the vertices of the W boson decays. Normally you would use the invisible phantom lines, but let's start with the visible dashes:
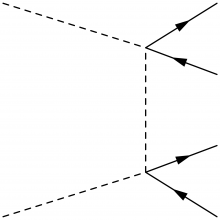
Notice the endpoints of the outgoing fermion lines are not horizontally aligned. This is solved by including the command \fmfstraight:
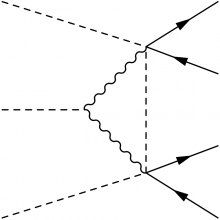
Use \fmffreeze to freeze this part of the diagram. This will prevent the next lines we add from ruining this balance. Now put back the rest (H → WW).
Now simple use phantom to make the help lines invisible. Note the use of tension, which needs to be fine-tuned:
\begin{fmffile}{feyngraph} \begin{fmfgraph}(150,150) \fmfstraight \fmfleft{i0,i1,i2} \fmfright{o1,o2,o3,o4} % outgoing fermions \fmf{fermion}{o1,v21,o2} \fmf{fermion}{o3,v22,o4} % phantoms to pull back fermion lines \fmf{phantom}{i0,v21} \fmf{phantom,tension=0.5}{v21,v22} \fmf{phantom}{i2,v22} \fmffreeze % H -> WW \fmf{dashes,tension=1.5}{i1,v1} \fmf{boson}{v1,v21} \fmf{boson}{v1,v22} \end{fmfgraph} \end{fmffile}
Forcing vertices at desired (x,y) positions
If you do not like puzzling with phantom lines and tension, you could force the vertex at an exact location using \fmfforce{(0.4w,0.7h)}{v}, which places the vertex v at the x position that is 40% of the width from the left, and at the y position that is 70% of the height from the bottom. (Note however that the feynMF manual states it should be used as a last resort only.) The alternative is to use intermediate mode with MetaPost which is explained in a section below.
It is also possible to use \fmfshift to shift vertices. This can be used for outgoing point created with \fmfleft etc., but also internal vertices after they have been frozen with \fmffreeze.
\begin{fmffile}{feyngraph} \begin{fmfgraph}(150,150) \fmfstraight \fmfleft{i} \fmfright{o1,o2,o3,o4} % force vertex locations \fmfforce{(0.40w,0.50h)}{v} \fmfforce{(0.68w,0.20h)}{v1} \fmfforce{(0.68w,0.80h)}{v2} % H -> WW \fmf{dashes,tension=1.5}{i,v} \fmf{boson}{v,v1} \fmf{boson}{v,v2} % outgoing fermions \fmf{fermion}{o1,v1,o2} \fmf{fermion}{o3,v2,o4} \end{fmfgraph} \end{fmffile}
Adding momentum arrows
The easiest and most economic way to add momentum arrows next to a leg is by using the following predefined command in the preamble (source):
\newcommand{\marrow}[5]{% \fmfcmd{style_def marrow#1 expr p = drawarrow subpath (1/4, 3/4) of p shifted 6 #2 withpen pencircle scaled 0.4; label.#3(btex #4 etex, point 0.5 of p shifted 6 #2); enddef;} \fmf{marrow#1,tension=0}{#5}}
This predefined command \marrow makes use of \fmfcmd which draws an fermion line (plain line with arrow) in MetaPost. \marrow needs five parameters (#1–#5):
- unique label of the arrow object (containing only letters);
- postion of the momentum arrow w.r.t. the particle leg:
down,up; - position of the label w.r.t. momentum arrow (optional):
bot,top; - label text drawn with the arrow (optional);
- comma-separated vertices between which the momentum arrow is drawn.
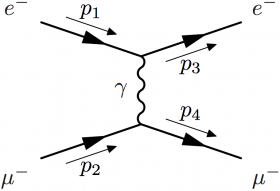
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i1,i2} \fmfright{o1,o2} \fmflabel{$e^-$}{i2} \fmflabel{$e^-$}{o2} \fmflabel{$\mu^-$}{i1} \fmflabel{$\mu^-$}{o1} \fmf{fermion}{i2,v2,o2} \marrow{ea}{ up }{top}{$p_1$}{i2,v2} \marrow{eb}{down}{bot}{$p_3$}{v2,o2} \fmf{fermion}{i1,v1,o1} \marrow{ma}{down}{bot}{$p_2$}{i1,v1} \marrow{mb}{ up }{top}{$p_4$}{v1,o1} \fmf{photon,label=$\gamma$}{v2,v1} \end{fmfgraph*} \end{fmffile}
Bent lines and loop
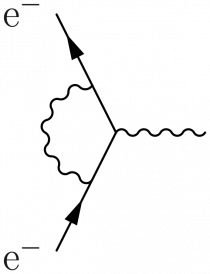
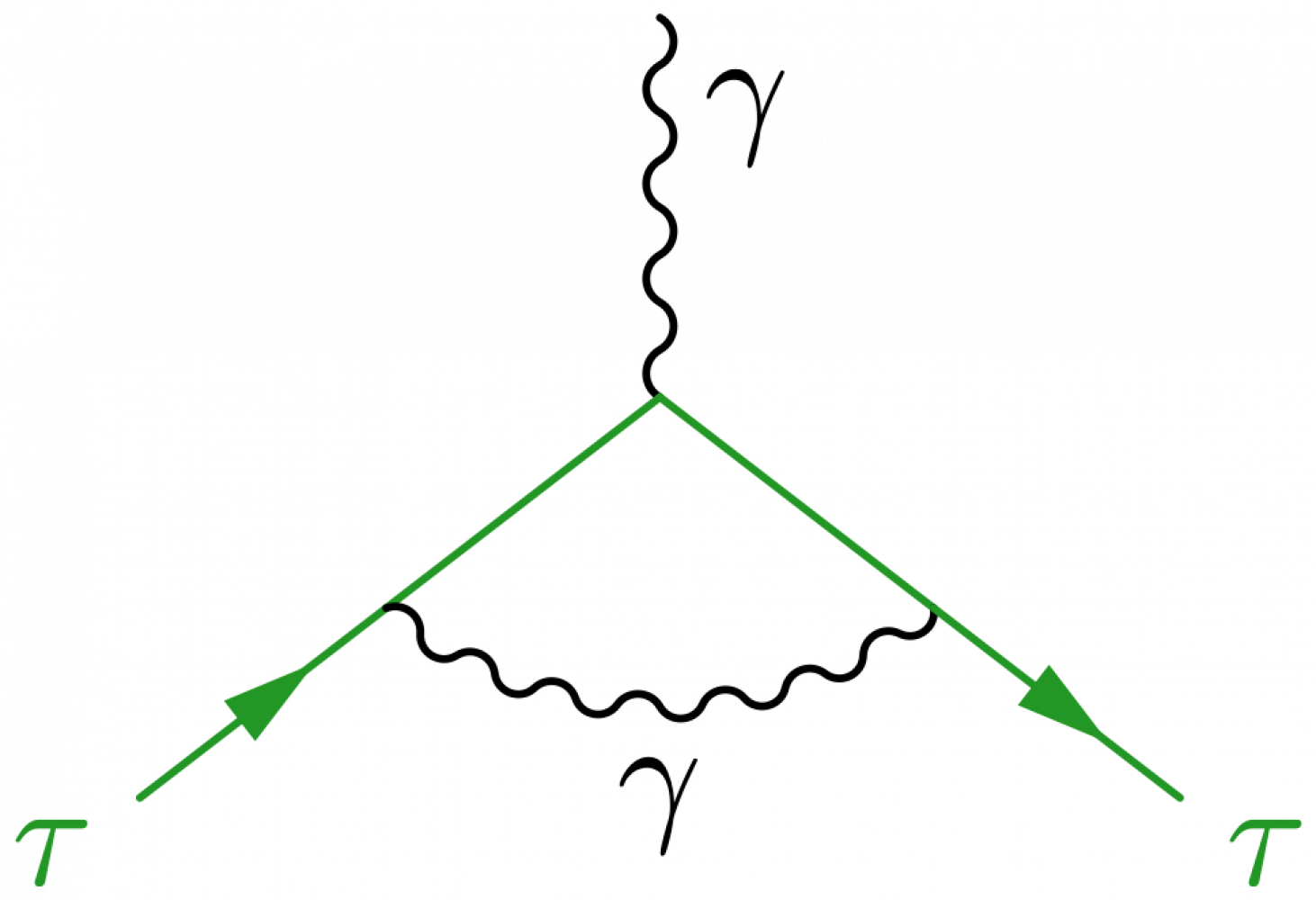
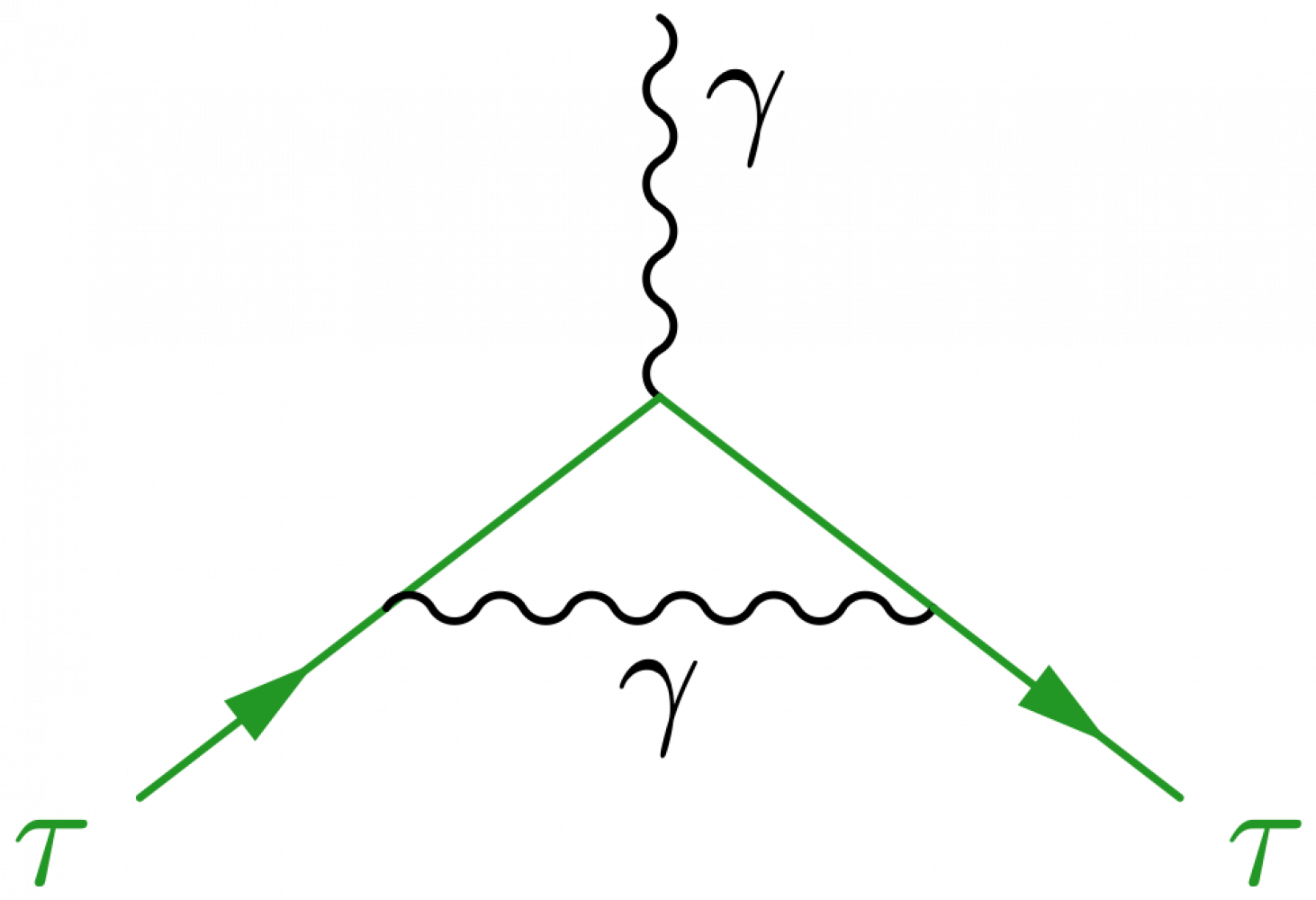
Lines can be bent by simply adding right or left. Here is for example the one-loop correction to the electron-photon vertex to compute the anomalous magnetic momentum:
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(70,100) \fmfleft{f2,f1} \fmfright{p} % outgoing photon \fmf{boson,l.s=left,t=0.8}{p,v} \fmf{fermion}{f2,v1} \fmf{plain,t=1.5}{v1,v,v2} \fmf{fermion}{v2,f1} \fmfv{l.a=165,l=e$^-$}{f1} % outcoming electron \fmfv{l.a=-165,l=e$^-$}{f2} % incoming electron \fmffreeze \fmf{boson,left}{v1,v2} % bend photon line to the left \end{fmfgraph*} \end{fmffile}
More examples can be found below in the sections on Higgs mass corrections and Penguin diagrams.
Intermediate mode: How to use MetaPost
If you don't like puzzling with phantom lines and tension, you can use \fmfforce as explained in a section above. You can gain even greater control by using feynMP's “intermediate mode” to use MetaPost more directly. \fmfipairs and \fmfiequ gives the ability to exactly position vertices, and \fmfi allow to draw straight and curved lines between these points.
The next level is executing MetaPost commands directly with \fmfcmd.
You can learn more about MetaPost in the manual or this tutorial. The feynmf manual and this paper contain some examples, and the author also put some advanced ones on this webpage. Examples on this wiki page that make use of MetaPost intermediately of directly are:
Vertices: MetaPost pairs
Vertices in the intermediate mode are declared as MetaPost pairs with \fmfpair. Then you can set them in several different ways: explicitly with some coordinates, along a path between two other pairs, sum of two pairs, … “feynMF vertices” declared with \fmfleft etc. can be accessed in MetaPost by prepending its name with two underscores; then they can be converted to a MetaPost pair using the vloc function. These different methods are shown below.
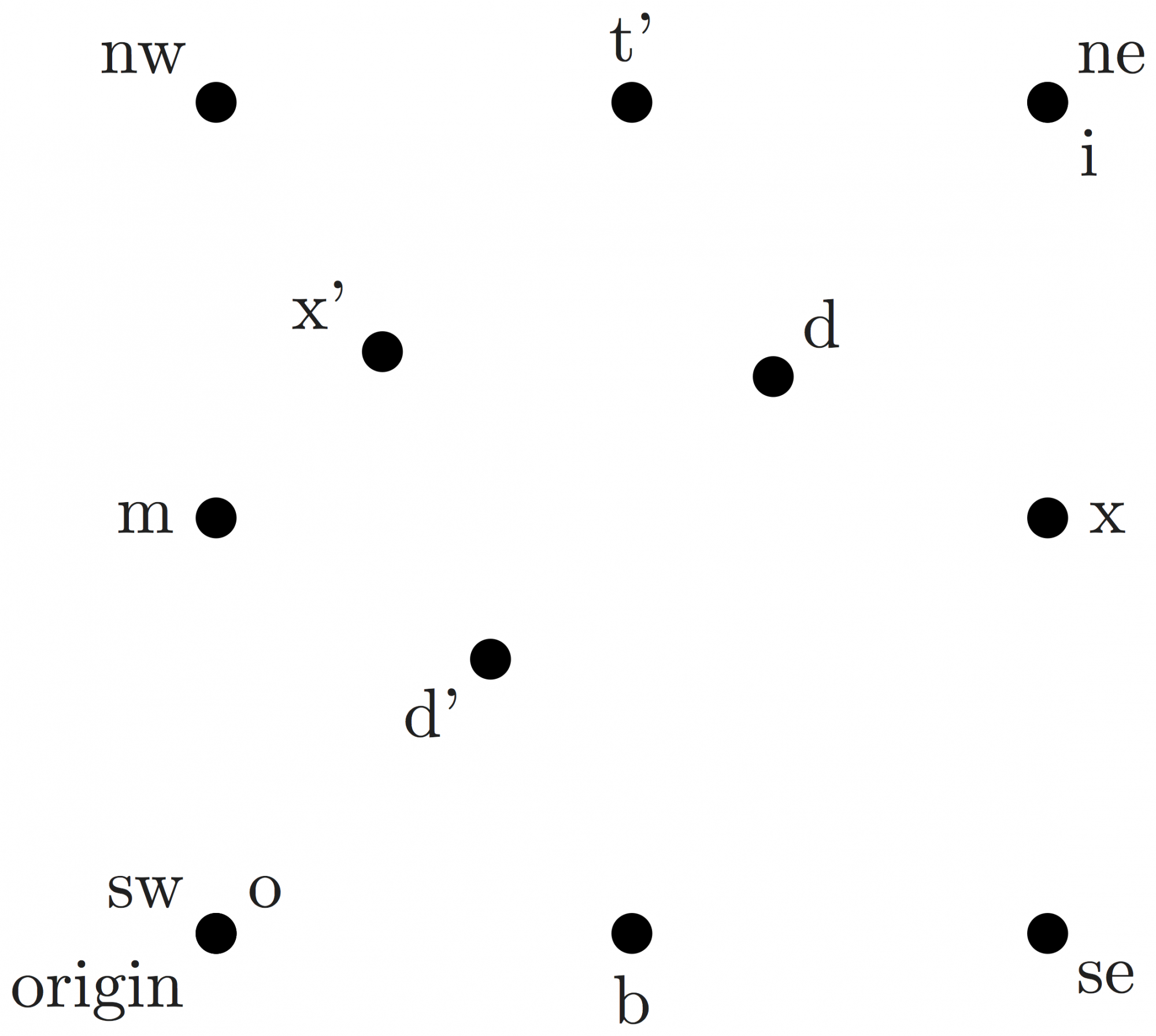
Note there are already some predefined points like origin and the cardinal directions ne (northeast), nw (northwest), se (southeast) and sw (southwest) for each corner.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,120) % predefined points (MetaPost pairs) \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=ne}{ne} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=nw}{nw} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=se}{se} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=sw,l.a=140}{sw} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=origin,l.a=-140}{origin} % new feynMF vertices \fmftop{t} \fmfbottom{b} % new MetaPost pairs \fmfipair{o,i,m,d,d',x,x',t'} \fmfiequ{o}{(0,0)} \fmfiequ{i}{(1w,1h)} \fmfiequ{m}{0.5[nw,sw]} \fmfiequ{d}{0.33[ne,sw]} \fmfiequ{d'}{0.33[sw,ne]} \fmfiequ{ypart(x)}{ypart(m)} \fmfiequ{xpart(x)}{xpart(.5[ne,se])} \fmfiequ{x'}{m+(.2w,.2h)} \fmfiequ{t'}{vloc(__t)} % new points labels \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=o,l.a=40}{o} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=i,l.a=-40}{i} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=m}{m} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=d}{d} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=d'}{d'} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=x}{x} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=x'}{x'} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=t'}{t'} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=b}{vloc(__b)} \end{fmfgraph*} \end{fmffile}
MetaPost paths
How do you connect vertices? Here is a straightforward example with MetaPost pairs using \fmfi:
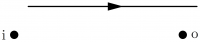
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,50) \fmfipair{i,o} \fmfiequ{i}{(0,0)} \fmfiequ{o}{(1w,0)} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=i,l.a=180}{i} \fmfiv{d.sh=circle,d.f=1,d.si=5pt,l=o,l.a=0}{o} \fmfi{fermion,l=path between MetaPost pairs,l.s=left}{i--o} \end{fmfgraph*} \end{fmffile}
You can now easily shift or rotate these paths:
\fmfi{fermion}{(i--o) shifted(10,-20)}
\fmfi{fermion}{(i--o) rotatedaround(i,45)}
An equivalent way is by using a vpath between two feynMF vertices by prepending the vertex name with two underscores so MetaPost can acces them:
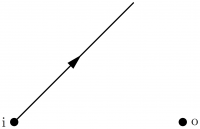
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,50) \fmfleft{i} \fmfright{o} \fmfdot{i,o} \fmflabel{i}{i} \fmflabel{o}{o} \fmf{phantom}{i,o} \fmfi{fermion,l=vpath between feynMP vertices,l.s=left}{vpath (__i,__o)} \end{fmfgraph*} \end{fmffile}
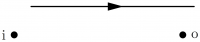
\fmfi{fermion}{vpath (__i,__o) shifted(10,-20)}
\fmfi{fermion}{vpath (__i,__o) rotatedaround(vloc(__i),45)}
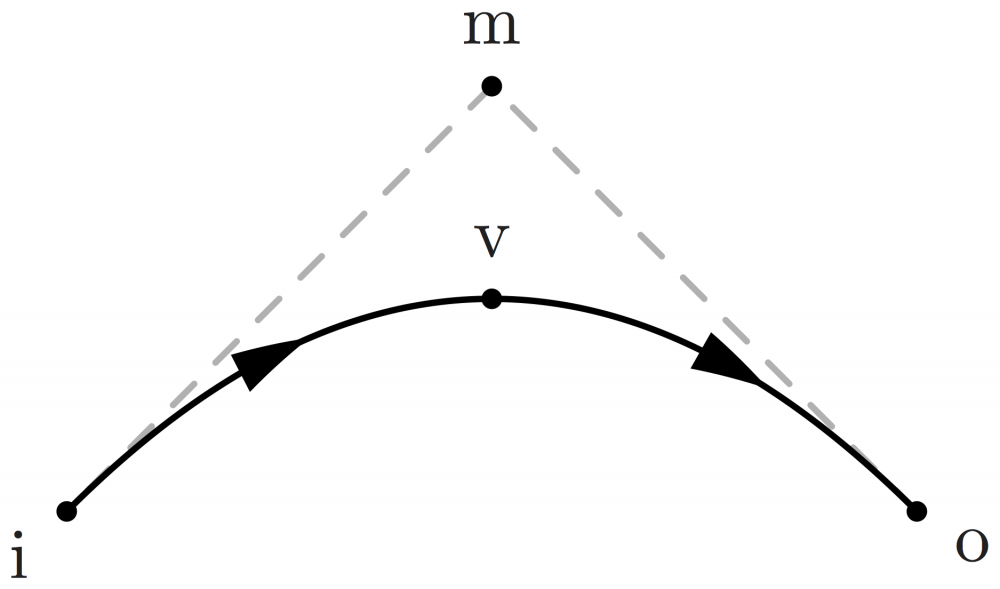
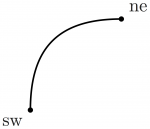
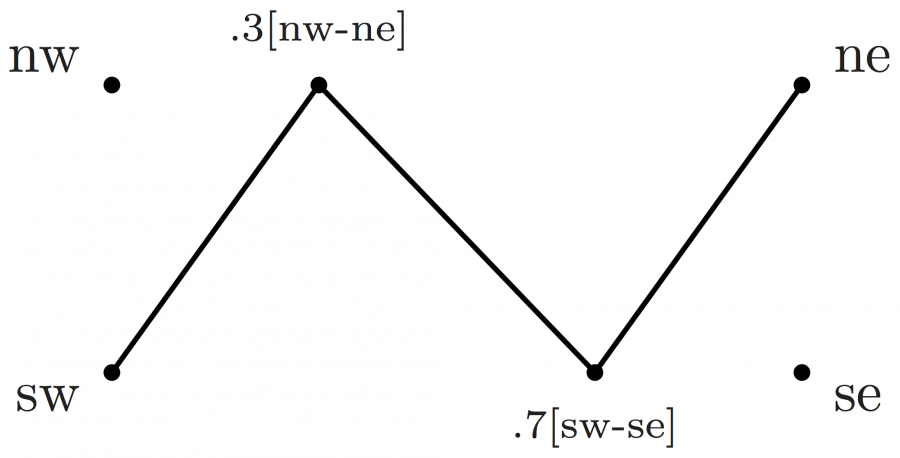
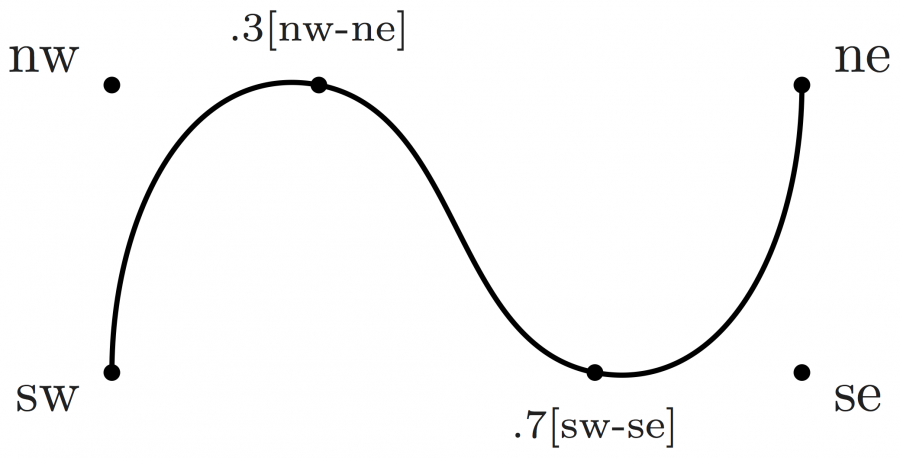
Here is an example of curved paths with i{m-i} .. {right}v drawing a path from i to v. The .. operator ensures a smooth connection. i{m-i} means that the line m-i is the tangent of the path starting on i's right side. {right}v means the path's right end arrives in vertex v's left side.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,60) \fmfipair{i,o,v,m} \fmfiequ{i}{(0,0)} \fmfiequ{o}{(w,0)} \fmfiequ{v}{(.5w,.5h)} \fmfiequ{m}{(.5w,h)} % grey tangent line (for illustration purposes) \fmfi{dashes,foreground=(0.7,,0.7,,0.7)}{m--i} \fmfi{dashes,foreground=(0.7,,0.7,,0.7)}{o--m} % curved paths \fmfi{fermion}{i{m-i} .. {right}v} \fmfi{fermion}{v{right} .. {o-m}o} % point labels \fmfiv{d.sh=circle,d.f=1,d.si=2pt,l=i}{i} \fmfiv{d.sh=circle,d.f=1,d.si=2pt,l=o}{o} \fmfiv{d.sh=circle,d.f=1,d.si=2pt,l=m}{m} \fmfiv{d.sh=circle,d.f=1,d.si=2pt,l=v,l.a=90}{v} \end{fmfgraph*} \end{fmffile}
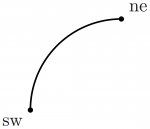
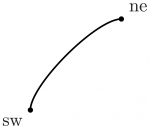
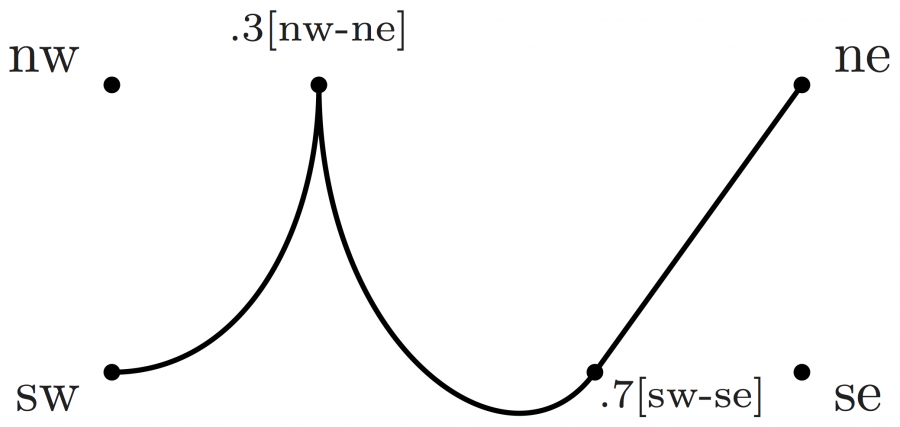
You can control a path's curvature by adding tension between two .. operators (less tension is more curvature):
Here are some examples from the aforementioned webpage making one long path:
Examples
Top quark pair production
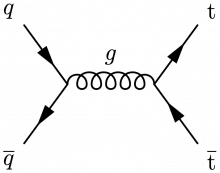
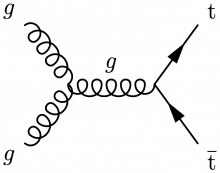
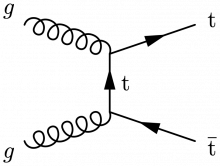
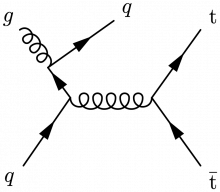
Some Feynman diagrams contributing to top quark pair production via gluon-gluon fusion:
Full code for a multipage PDF including all figures below can be found here.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i2,i1} \fmfright{o2,o1} % main \fmf{fermion}{i1,v1,i2} \fmf{fermion}{o2,v2,o1} \fmf{gluon,label=$g$,label.side=right,label.dist=10}{v2,v1} % labels \fmflabel{$q$}{i1} \fmflabel{$\overline{q}$}{i2} \fmflabel{$\overline{\text{t}}$}{o2} \fmflabel{t}{o1} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i2,i1} \fmfright{o2,o1} \fmfshift{2 left}{i1} \fmf{fermion}{o2,v2,o1} \fmf{gluon}{v1,i1} \fmf{gluon}{v1,i2} \fmf{gluon,label=$g$}{v1,v2} % labels \fmfv{l.d=4,l=$g$}{i1} \fmfv{l.d=6,l=$g$}{i2} \fmflabel{$\overline{\text{t}}$}{o2} \fmflabel{t}{o1} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i2,i1} \fmfright{o2,o1} % main \fmf{gluon}{v1,i1} \fmf{fermion}{v1,o1} \fmf{gluon}{i2,v2} \fmf{fermion}{o2,v2} \fmf{fermion,label=t}{v2,v1} % labels \fmflabel{$g$}{i2} \fmflabel{$g$}{i1} \fmfv{l.d=7,l.a=22,l=t}{o1} \fmfv{l.d=7,l.a=-20,l=$\overline{\text{t}}$}{o2} \end{fmfgraph*} \end{fmffile}
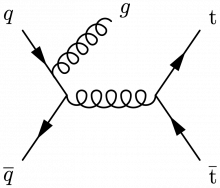
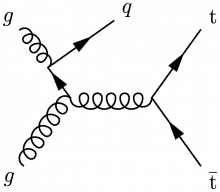
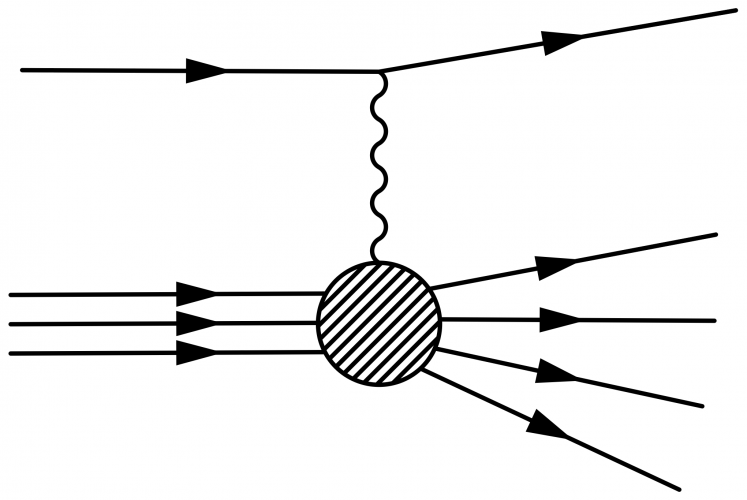
With radiated quarks or gluons that will form hard jets:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,70) \fmfleft{i2,i1} \fmfright{o2,o1} \fmftop{t} \fmfshift{5 up}{t} % skeleton \fmf{phantom}{i1,v1,i2} \fmf{phantom}{o1,v2,o2} \fmf{phantom}{v1,v2} \fmffreeze % main \fmf{fermion}{i1,g} \fmf{plain,tension=2.8}{g,v1} \fmf{fermion}{v1,i2} \fmf{gluon,tension=0}{t,g} \fmf{gluon}{v1,v2} \fmf{fermion}{o2,v2,o1} % labels \fmflabel{$q$}{i1} \fmflabel{$\overline{q}$}{i2} \fmfv{l.d=5,l.a=25,l=$g$}{t} \fmflabel{$\bar{\text{t}}$}{o2} \fmflabel{$\text{t}$}{o1} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,75) \fmfleft{i2,i1} \fmfright{o2,o1} \fmftop{t} \fmfshift{4 left}{i1} \fmfshift{2 left}{i2} \fmfshift{5 up}{t} % skeleton \fmf{phantom}{i1,v1,i2} \fmf{phantom}{o1,v2,o2} \fmf{phantom,tension=1.2}{v1,v2} \fmffreeze % main \fmf{gluon,tension=0.8}{g,i1} \fmf{fermion}{v1,g} \fmf{gluon}{v1,i2} \fmf{fermion,tension=0}{g,t} \fmf{gluon}{v1,v2} \fmf{fermion}{o2,v2,o1} % labels \fmfv{l.d=4,l=$g$}{i1} \fmfv{l.d=6,l=$g$}{i2} \fmfv{l.d=5,l.a=25,l=$q$}{t} \fmflabel{$\bar{\text{t}}$}{o2} \fmflabel{$\text{t}$}{o1} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,75) \fmfleft{i2,i1} \fmfright{o2,o1} \fmftop{t} \fmfshift{4 left}{i1} \fmfshift{2 left}{i2} \fmfshift{5 up}{t} % skeleton \fmf{phantom}{i1,v1,i2} \fmf{phantom}{o1,v2,o2} \fmf{phantom,tension=1.2}{v1,v2} \fmffreeze % main \fmf{gluon,tension=0.8}{g,i1} \fmf{fermion}{v1,g} \fmf{fermion}{i2,v1} \fmf{fermion,tension=0}{g,t} \fmf{gluon}{v1,v2} \fmf{fermion}{o2,v2,o1} % labels \fmfv{l.d=4,l=$g$}{i1} \fmfv{l.d=6,l=$q$}{i2} \fmfv{l.d=5,l.a=25,l=$q$}{t} \fmflabel{$\bar{\text{t}}$}{o2} \fmflabel{$\text{t}$}{o1} \end{fmfgraph*} \end{fmffile}
Drell-Yan plus jet production
A simple one:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) %\fmfset{arrow_len}{10} \fmfleft{i2,i1} \fmfright{o2,o1} \fmf{fermion}{i1,v1,i2} \fmf{fermion}{o2,v2,o1} \fmf{boson,label=$\text{Z}/\gamma^*$,label.side=right}{v1,v2} \fmflabel{$q$}{i1} \fmflabel{$\overline{q}$}{i2} \fmflabel{$\ell^+$}{o2} \fmflabel{$\ell^-$}{o1} \end{fmfgraph*} \end{fmffile}
Some variants of Drell-Yan plus jets.
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(125,75) \fmfleft{i2,i1} \fmfright{o2,o1} \fmftop{t} \fmf{phantom}{i1,v1,i2} \fmf{phantom}{o1,v2,o2} \fmf{phantom}{v1,v2} \fmffreeze \fmfshift{5 left}{i1} \fmfshift{5 up}{i1,t} \fmf{gluon,tension=0.8}{g,i1} \fmf{fermion}{v1,g} \fmf{fermion}{i2,v1} \fmf{fermion,tension=0}{g,t} \fmf{boson,label=$\text{Z}/\gamma^*$,label.side=right}{v1,v2} \fmf{fermion}{o2,v2,o1} \fmflabel{$g$}{i1} \fmflabel{$q$}{i2} \fmfv{l.a=25,l=$q$}{t} \fmflabel{$\ell^+$}{o2} \fmflabel{$\ell^-$}{o1} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,70) \fmfleft{i2,i1} \fmfright{o2,o1} \fmftop{t} \fmf{phantom}{i1,v1,i2} \fmf{phantom}{o1,v2,o2} \fmf{phantom}{v1,v2} \fmffreeze \fmf{fermion}{i1,g} \fmf{plain,tension=2.8}{g,v1} \fmf{fermion}{v1,i2} \fmf{gluon,tension=0}{t,g} \fmf{boson,label=$\text{Z}/\gamma^*$,label.side=right}{v1,v2} \fmf{fermion}{o2,v2,o1} \fmflabel{$q$}{i1} \fmflabel{$q'$}{i2} \fmflabel{$\ell^+$}{o2} \fmflabel{$\ell^-$}{o1} \end{fmfgraph*} \end{fmffile}
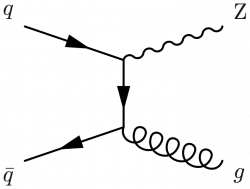
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i2,i1} \fmfright{o2,o1} \fmflabel{$q$}{i1} \fmflabel{$\bar{q}$}{i2} \fmf{fermion}{i1,v1,v2,i2} \fmflabel{$g$}{o2} \fmflabel{Z}{o1} \fmf{photon}{v1,o1} \fmf{gluon}{v2,o2} \end{fmfgraph*} \end{fmffile}
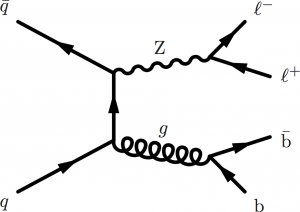
Z boson with two b jets.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,90) \fmfpen{thick} \fmfleftn{i}{2} \fmfrightn{o}{4} %particelle entranti \fmf{fermion}{i1,v1} \fmf{fermion}{v2,i2} \fmflabel{$\bar{q}$}{i2} \fmflabel{$q$}{i1} %mediatore \fmf{fermion}{v1,v2} %%% produzione Z \fmf{photon,label=Z}{v2,v4} % produzione l l \fmf{fermion}{v4,o4} \fmf{fermion}{o3,v4} \fmflabel{$\ell^+$}{o3} \fmflabel{$\ell^-$}{o4} %%% produzione glume \fmf{gluon,label=$g$}{v1,v3} %produzione b b \fmf{fermion}{v3,o2} \fmf{fermion}{o1,v3} \fmflabel{$\bar{\text{b}}$}{o2} \fmflabel{b}{o1} \end{fmfgraph*} \end{fmffile}
W plus jet production
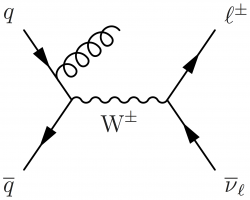
Two simple ones:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,70) \fmfleft{i2,i1} \fmfright{o2,o1} \fmftop{t} \fmf{phantom}{i1,v1,i2} \fmf{phantom}{o1,v2,o2} \fmf{phantom}{v1,v2} \fmffreeze \fmf{fermion}{i1,g} \fmf{plain,tension=2.8}{g,v1} \fmf{fermion}{v1,i2} \fmf{gluon,tension=0}{t,g} \fmf{boson,label=$\text{W}^\pm$,label.side=right}{v1,v2} \fmf{fermion}{o2,v2,o1} \fmflabel{$q$}{i1} \fmflabel{$\overline{q}$}{i2} \fmflabel{$\ell^\pm$}{o1} \fmflabel{$\overline{\nu}_\ell$}{o2} \end{fmfgraph*} \end{fmffile}
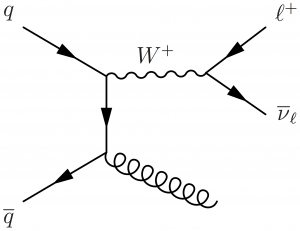
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,90) \fmfstraight \fmfleft{i2,i1} \fmfright{o1,l2,l1} % skeleton \fmf{phantom,tension=1.8}{i1,v1} \fmf{phantom,tension=1.0}{v1,l1} \fmf{phantom,tension=1.8}{v1,v2} \fmf{phantom,tension=1.8}{i2,v2} \fmf{phantom,tension=1.0}{v2,o1} \fmffreeze % W + jets \fmfshift{5 right}{l1,l2} \fmfshift{20 left}{o1} % quarks \fmflabel{$q$}{i1} \fmflabel{$\overline{q}$}{i2} \fmf{fermion}{i1,v1,v2,i2} % W boson \fmf{boson,tension=1.2,label=$W^+$,label.side=left}{v1,z} \fmf{gluon}{v2,o1} % leptons \fmflabel{$\ell^+$}{l1} \fmflabel{$\overline{\nu}_\ell$}{l2} \fmf{fermion}{l1,z,l2} \end{fmfgraph*} \end{fmffile}
Higgs boson production
Here are some examples of Higgs production in proton-proton collisions. For more Higgs related diagrams and plots, check out this summary paper by ATLAS and CMS with a gallery of Feynman diagrams, or this LHC TWiki page with high resolution cross section and branching ratio plots.
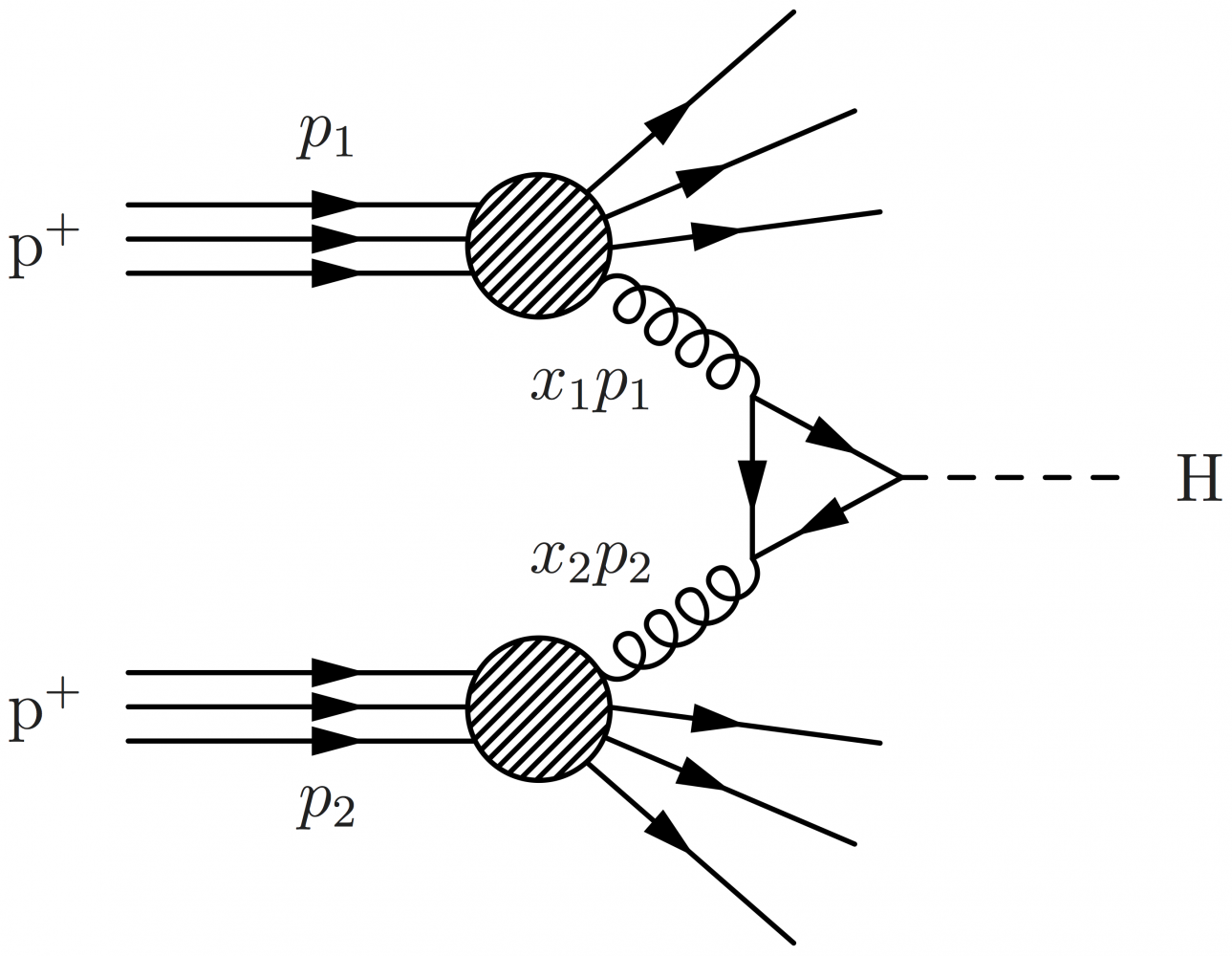
Gluon fusion
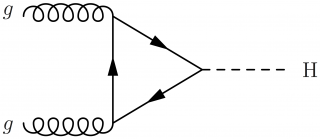
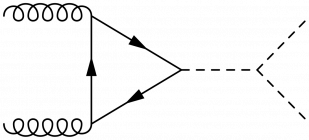
Higgs boson production via gluon-gluon fusion with a fermion triangle loop:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,60) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,h,o2} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=0.5}{t1,o1} \fmf{phantom,tension=0.5}{t2,o2} \fmffreeze % top loop \fmf{fermion,tension=1}{t1,t2,t3,t1} % Higgs boson \fmf{dashes,tension=2.0}{t3,h} % labels \fmflabel{$g$}{i1} \fmflabel{$g$}{i2} \fmflabel{H}{h} \end{fmfgraph*} \end{fmffile}
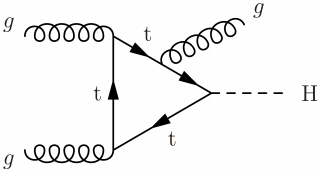
Including final-state gluon radiation:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(140,120) \fmfstraight \fmfleft{d,i1,d,i2,d} \fmfright{d,o1,h,o2,o3} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=0.5}{t1,o1} \fmf{phantom,tension=0.5}{t2,o2} \fmffreeze % top loop \fmf{phantom,tension=0.8}{t1,t2,t3,t1} \fmf{fermion,tension=0,label=t,label.side=left}{t3,t1,t2} %\fmf{fermion,tension=0.01,label=t,label.side=left}{t2,r1,t3} \fmf{fermion,tension=0.001,label=t,label.side=left}{t2,r1} \fmf{fermion,tension=0.001}{r1,t3} % Higgs boson \fmf{dashes,tension=2}{t3,h} \fmffreeze % radiated gluon pulled by phantoms \fmf{gluon,tension=1.4}{r2,r1} \fmf{phantom,tension=1.5}{r2,o3} % pull up \fmf{phantom,tension=1.0}{r2,o2} % pull down % labels \fmflabel{$g$}{i1} \fmflabel{$g$}{i2} \fmflabel{$g$}{r2} \fmflabel{H}{h} \end{fmfgraph*} \end{fmffile}
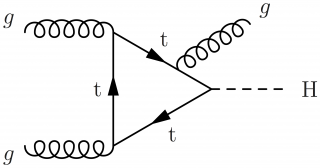
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(140,120) \fmfstraight \fmfleft{d,i1,d,i2,d} \fmfright{d,o1,h,o2,o3} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=0.5}{t1,o1} \fmf{phantom,tension=0.5}{t2,o2} \fmffreeze % Higgs boson \fmf{dashes,tension=2}{t3,h} % top loop \fmf{phantom,tension=0.8}{t1,t2,t3,t1} \fmffreeze \fmf{fermion,tension=1,label=t,label.side=left}{t3,t1,t2,tm} \fmf{plain,tension=5}{tm,t3} \fmffreeze % radiated gluon pulled by phantoms \fmf{phantom,tension=1}{t2,r1} % offset vertex \fmf{phantom,tension=2}{r1,t3} % offset vertex \fmffreeze \fmf{gluon,tension=1.4}{r2,r1} \fmf{phantom,tension=1.5}{r2,o3} % pull up \fmf{phantom,tension=1.0}{r2,o2} % pull down % labels \fmflabel{$g$}{i1} \fmflabel{$g$}{i2} \fmflabel{$g$}{r2} \fmflabel{H}{h} \end{fmfgraph*} \end{fmffile}
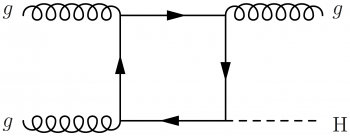
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(170,60) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,o2} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=0.92}{t1,t4} \fmf{phantom,tension=0.92}{t2,t3} % Higgs boson and gluon radiation \fmf{dashes,tension=1}{t4,o1} \fmf{gluon,tension=1}{o2,t3} % top loop \fmf{fermion,tension=0}{t1,t2,t3,t4,t1} % labels \fmflabel{$g$}{i1} \fmflabel{$g$}{i2} \fmflabel{H}{o1} \fmflabel{$g$}{o2} \end{fmfgraph*} \end{fmffile}
Vector boson fusion
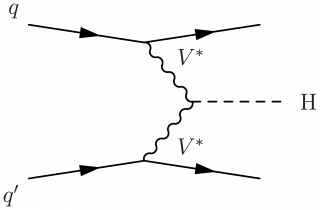
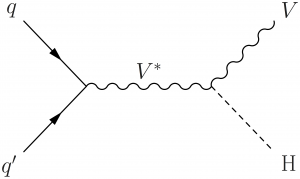
Some variations of Higgs boson production in vector boson fusion, where V can be a Z or W boson:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,80) \fmfleft{i1,i3} \fmfright{o1,o2,o3} \fmf{fermion}{i1,v1,o1} \fmf{fermion}{i3,v3,o3} \fmf{phantom,tension=0.3}{v1,v3} \fmffreeze \fmf{boson,label=$V$,label.side=left}{v3,v2,v1} \fmf{dashes}{v2,o2} \fmflabel{$q$}{i3} \fmflabel{$q'$}{i1} \fmflabel{H}{o2} \end{fmfgraph*} \end{fmffile}
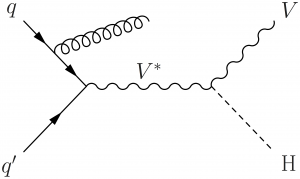
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,90) \fmfleft{d,i1,d,d,i3,d} \fmfright{o1,d,o2,d,o3} \fmf{fermion}{i1,v1,o1} \fmf{fermion}{i3,v3,o3} \fmf{phantom,tension=0.3}{v1,v3} \fmffreeze \fmf{boson,label=$V^*$,label.side=left,tension=0.7}{v3,v2,v1} \fmf{dashes}{v2,o2} \fmflabel{$q$}{i3} \fmflabel{$q'$}{i1} \fmflabel{H}{o2} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,60) %\fmfstraight \fmfleft{i1,i3} \fmfright{o1,o2,o3} \fmf{fermion}{i1,v1,o1} \fmf{fermion}{i3,v3,o3} \fmffreeze \fmf{boson,label=$V$,label.side=left}{v3,v2,v1} \fmffreeze \fmf{dashes}{v2,o2} \fmflabel{$q$}{i3} \fmflabel{$q'$}{i1} \fmflabel{H}{o2} \end{fmfgraph*} \end{fmffile}
Higgs Strahlung
Some variation of Higgs boson production in Higgs Strahlung, including diagrams with gluon radiation and ZH production in gluon-gluon fusion:
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,60) \fmfleft{i1,i2} \fmfright{o1,o2} \fmf{fermion}{i1,v1} \fmf{fermion}{i2,v1} \fmf{boson,label=$V^*$,label.side=left}{v1,v2} \fmf{boson,label.side=left}{v2,o2} \fmf{dashes}{v2,o1} \fmflabel{$q'$}{i1} \fmflabel{$q$}{i2} \fmflabel{$V$}{o2} \fmflabel{H}{o1} \end{fmfgraph*} \end{fmffile}
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(240,100) \fmfset{wiggly_len}{18} \fmfleft{i1,i2} \fmfright{o1,o2} \fmf{fermion}{i1,v1} \fmf{fermion}{i2,v1} \fmf{boson,label=$V^*$,label.side=left}{v1,v2} \fmf{boson,label.side=left}{v2,o2} \fmf{dashes}{v2,o1} \fmflabel{$q'$}{i1} \fmflabel{$q$}{i2} \fmflabel{$V$}{o2} \fmflabel{H}{o1} \end{fmfgraph*} \end{fmffile}
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(240,100) \fmfset{wiggly_len}{18} \fmfleft{i1,i2} \fmfright{o1,o2} \fmftop{t1} \fmf{fermion}{i1,v1} \fmf{fermion,tension=2}{i2,s2,v1} \fmf{boson,label=$V^*$,label.side=left}{v1,v2} \fmf{boson,label.side=left}{v2,o2} \fmf{dashes}{v2,o1} \fmffreeze \fmf{gluon}{t1,s2} \fmflabel{$q'$}{i1} \fmflabel{$q$}{i2} %\fmflabel{$g$}{t1} \fmflabel{$V$}{o2} \fmflabel{H}{o1} \end{fmfgraph*} \end{fmffile}
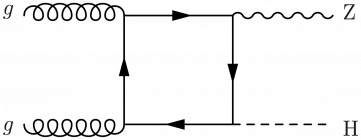
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(170,60) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,m,o2} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=0.4}{t1,o1} \fmf{phantom,tension=0.4}{t2,o2} \fmffreeze % top loop \fmf{fermion,tension=1}{t1,t2,t3,t1} \fmf{phantom,tension=1.4}{t3,m} \fmffreeze % Higgs boson \fmf{boson,tension=1.4,label=Z$^*$}{t3,h} \fmf{dashes,tension=1}{h,o1} \fmf{boson,tension=1}{h,o2} % labels \fmflabel{$g$}{i1} \fmflabel{$g$}{i2} \fmflabel{H}{o1} \fmflabel{Z}{o2} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(170,60) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,o2} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=0.92}{t1,t4} \fmf{phantom,tension=0.92}{t2,t3} % Higgs boson \fmf{dashes,tension=1}{t4,o1} \fmf{boson,tension=1}{t3,o2} % top loop \fmf{fermion,tension=0}{t1,t2,t3,t4,t1} % labels \fmflabel{$g$}{i1} \fmflabel{$g$}{i2} \fmflabel{H}{o1} \fmflabel{Z}{o2} \end{fmfgraph*} \end{fmffile}
Associated production
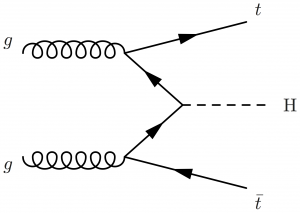
Associated production of Higgs boson production with a top quark pair:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(140,90) \fmfleft{d,i1,d,d,i3,d} \fmfright{o1,d,o2,d,o3} \fmf{gluon,tension=1.2}{i1,v1} \fmf{gluon,tension=1.2}{v3,i3} \fmf{fermion}{o1,v1} \fmf{fermion}{v3,o3} \fmf{phantom,tension=0.3}{v1,v3} \fmffreeze \fmf{fermion}{v1,v2,v3} \fmf{dashes,tension=1.3}{v2,o2} \fmflabel{$g$}{i3} \fmflabel{$g$}{i1} \fmflabel{$t$}{o3} \fmflabel{$\bar{t}$}{o1} \fmflabel{H}{o2} \end{fmfgraph*} \end{fmffile}
Higgs boson pair production via gluon-gluon fusion
Triangle diagram of gluon-gluon fusion to produce a pair of Higgs bosons.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(170,60) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,m,o2} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=0.4}{t1,o1} \fmf{phantom,tension=0.4}{t2,o2} \fmffreeze % top loop \fmf{fermion,tension=1}{t1,t2,t3,t1} \fmf{phantom,tension=1.4}{t3,m} \fmffreeze % Higgs boson \fmf{dashes,tension=1.4}{t3,h} \fmf{dashes,tension=1}{h,o1} \fmf{dashes,tension=1}{h,o2} \end{fmfgraph*} \end{fmffile}
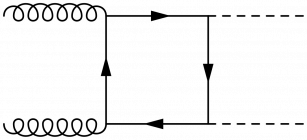
A box diagram of gluon-gluon fusion producing a pair of Higgs bosons.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(170,60) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,o2} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=1}{t1,t4} \fmf{phantom,tension=1}{t2,t3} % Higgs boson \fmf{dashes,tension=1}{t4,o1} \fmf{dashes,tension=1}{t3,o2} % top loop \fmf{fermion,tension=0}{t1,t2,t3,t4,t1} \end{fmfgraph*} \end{fmffile}
Beyond the Standard model
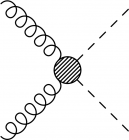
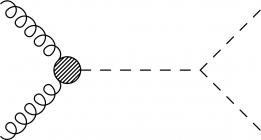
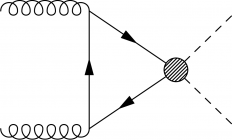
For effective field, unknown or generalized processes beyond the Standard Model (BSM), one can introduce blobs of some size at some vertex with \fmfblob.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(80,80) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,o2} % gluons \fmf{gluon}{i1,v} \fmf{gluon}{v,i2} \fmfblob{20}{v} % Higgs boson \fmf{dashes,tension=1}{v,o1} \fmf{dashes,tension=1}{v,o2} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(130,80) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,o2} % gluons \fmf{gluon}{i1,v} \fmf{gluon}{v,i2} \fmfblob{20}{v} % Higgs boson \fmf{dashes,tension=1}{v,h} \fmf{dashes,tension=1}{h,o1} \fmf{dashes,tension=1}{h,o2} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,60) \fmfstraight \fmfleft{i1,i2} \fmfright{o1,o2} % gluons \fmf{gluon}{i1,t1} \fmf{gluon}{t2,i2} \fmf{phantom,tension=0.6}{t1,o1} \fmf{phantom,tension=0.6}{t2,o2} \fmffreeze % top loop \fmf{fermion,tension=0.70}{t1,t2,t3,t1} % Higgs boson \fmf{dashes,tension=1}{t3,o1} \fmf{dashes,tension=1}{t3,o2} \fmfblob{20}{t3} \end{fmfgraph*} \end{fmffile}
Pseudoscalar Higgs boson
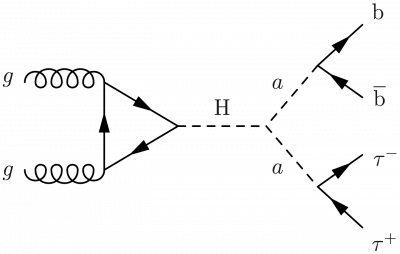
Here are some examples of processes with a pseudoscalar Higgs boson a from a two Higgs doublet model (2HDM).
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(130,130) \fmfleft{d,d,g2,d,g1,d,d} \fmfright{b2,d,t2,d,t1,d,b1} \fmf{gluon,tension=2}{v1,g1} \fmf{gluon,tension=2}{g2,v2} \fmf{phantom}{v1,t1} \fmf{phantom}{v2,t2} \fmffreeze \fmf{fermion}{b2,v2,v3,v1,b1} \fmf{dashes,tension=1.5,label=$a$,l.s=left}{v3,a} \fmf{fermion}{t2,a,t1} \fmflabel{$g$}{g1} \fmflabel{$g$}{g2} \fmflabel{$\tau^-$}{t1} \fmflabel{$\tau^+$}{t2} \fmflabel{b}{b1} \fmflabel{$\overline{\text{b}}$}{b2} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(180,140) \fmfstraight \fmfleft{i2,g2,g1,i1} \fmfright{o4,o3,o2,o1} \fmftop{top} \fmfbottom{bot} % gluon \fmf{gluon,tension=2.6}{t1,g1} \fmf{gluon,tension=2.6}{g2,t2} \fmf{phantom,tension=0.4}{o1,t1,o3} \fmf{phantom,tension=0.4}{o2,t2,o4} \fmffreeze % top loop \fmf{fermion,tension=1.0}{t1,t3,t2,t1} \fmf{phantom,tension=0.4}{o3,t3,o2} \fmffreeze % Higgs bosons \fmf{dashes,tension=1.4,label=H,l.s=left}{t3,h} \fmf{dashes,tension=1.2,label=$a$,l.s=right}{v1,h,v2} % decay products \fmf{phantom,tension=0.8}{top,v1} \fmf{phantom,tension=0.8}{v2,bot} \fmfshift{16 down}{o1} \fmfshift{ 8 down}{o2} \fmfshift{ 8 up}{o3} \fmfshift{16 up}{o4} \fmf{fermion,tension=1.8}{o2,v1,o1} \fmf{fermion,tension=1.8}{o4,v2,o3} % labels \fmflabel{$g$}{g1} \fmflabel{$g$}{g2} \fmflabel{$\text{b}$}{o1} \fmflabel{$\overline{\text{b}}$}{o2} \fmflabel{$\tau^-$}{o3} \fmflabel{$\tau^+$}{o4} \end{fmfgraph*} \end{fmffile}
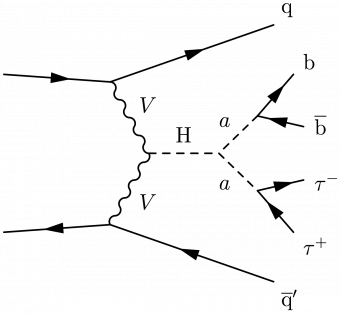
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(170,140) %\fmfstraight \fmfleft{d,i2,d,d,i1,d} \fmfright{q2,t2,t1,b2,b1,q1} \fmftop{top} \fmfbottom{bot} % quarks \fmf{fermion,tension=1.9}{i1,v1} \fmf{fermion,tension=1.9}{v2,i2} \fmf{fermion}{v1,q1} \fmf{fermion}{q2,v2} % vector bosons \fmf{boson,label=$V$,label.side=left}{v1,h,v2} % Higgs bosons \fmf{dashes,tension=1.1,label=H,label.side=left}{h,a} \fmf{dashes,label=$a$,label.side=right}{b,a,t} \fmf{fermion}{t2,t,t1} \fmf{fermion}{b2,b,b1} \fmf{phantom,tension=0.4}{top,b,t,bot} %\fmfshift{10 right}{b1,b2,t1,t2} % label \fmflabel{$\text{b}$}{b1} \fmflabel{$\overline{\text{b}}$}{b2} \fmflabel{$\tau^-$}{t1} \fmflabel{$\tau^+$}{t2} \fmflabel{$\text{q}$}{q1} \fmflabel{$\overline{\text{q}}'$}{q2} \end{fmfgraph*} \end{fmffile}
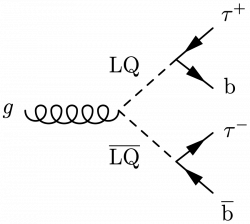
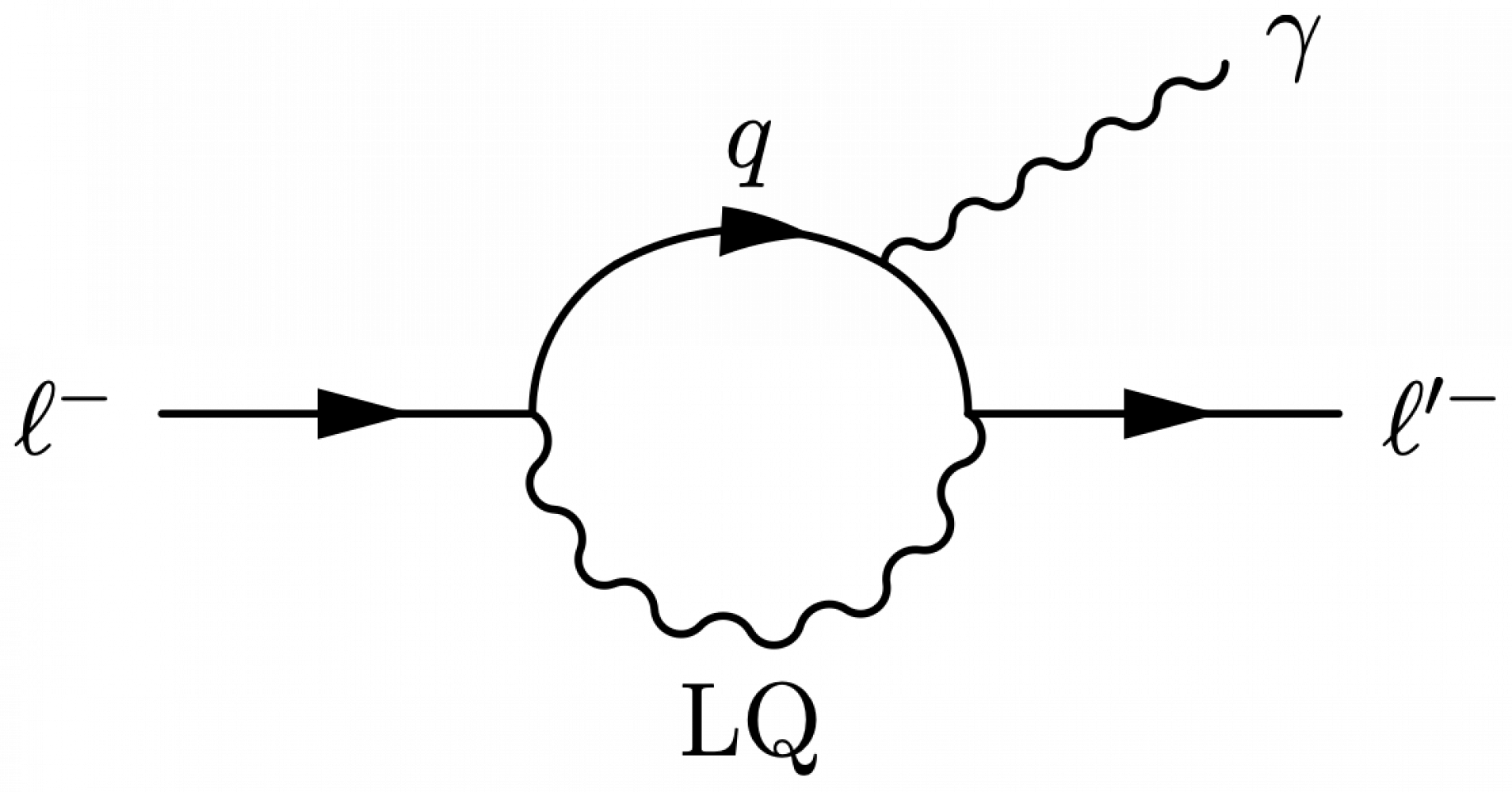
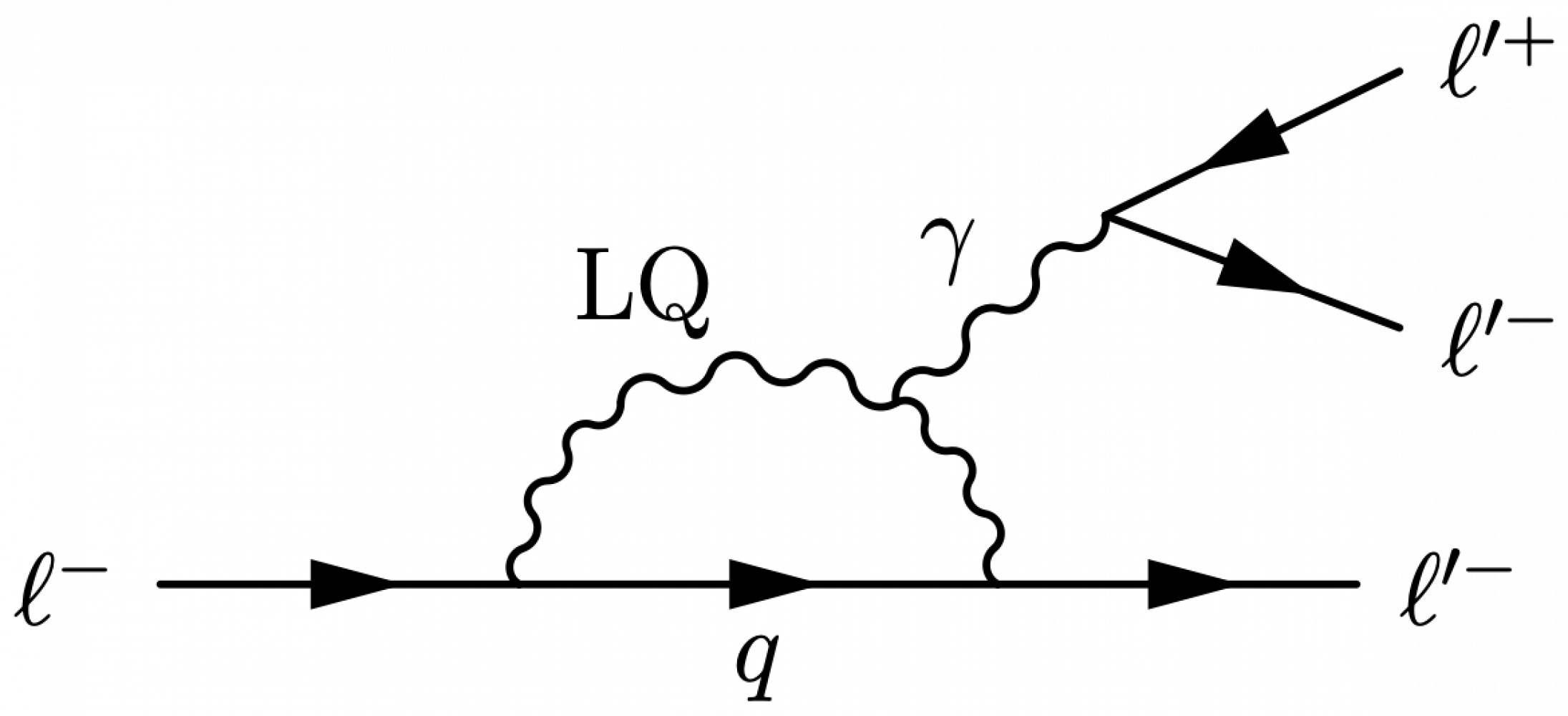
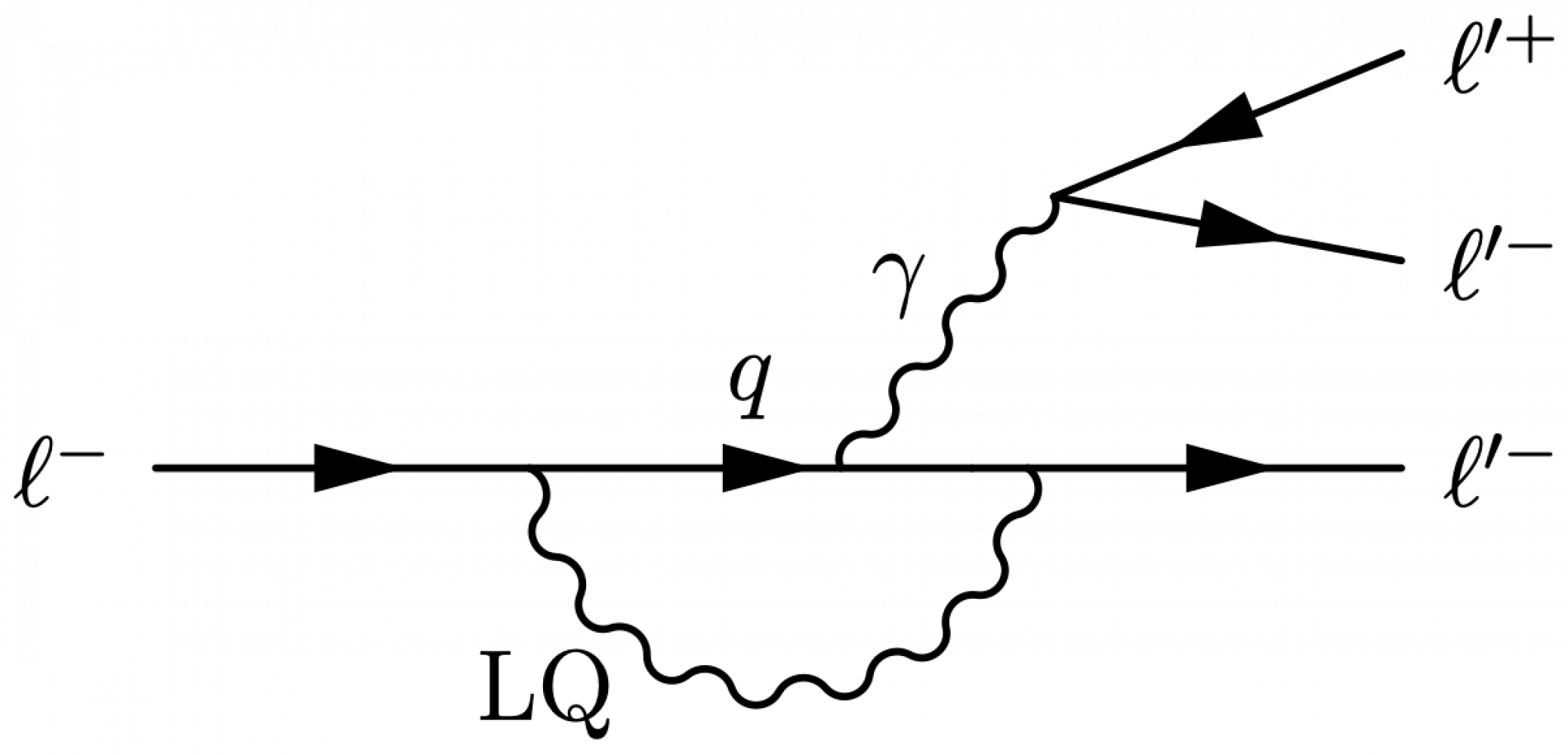
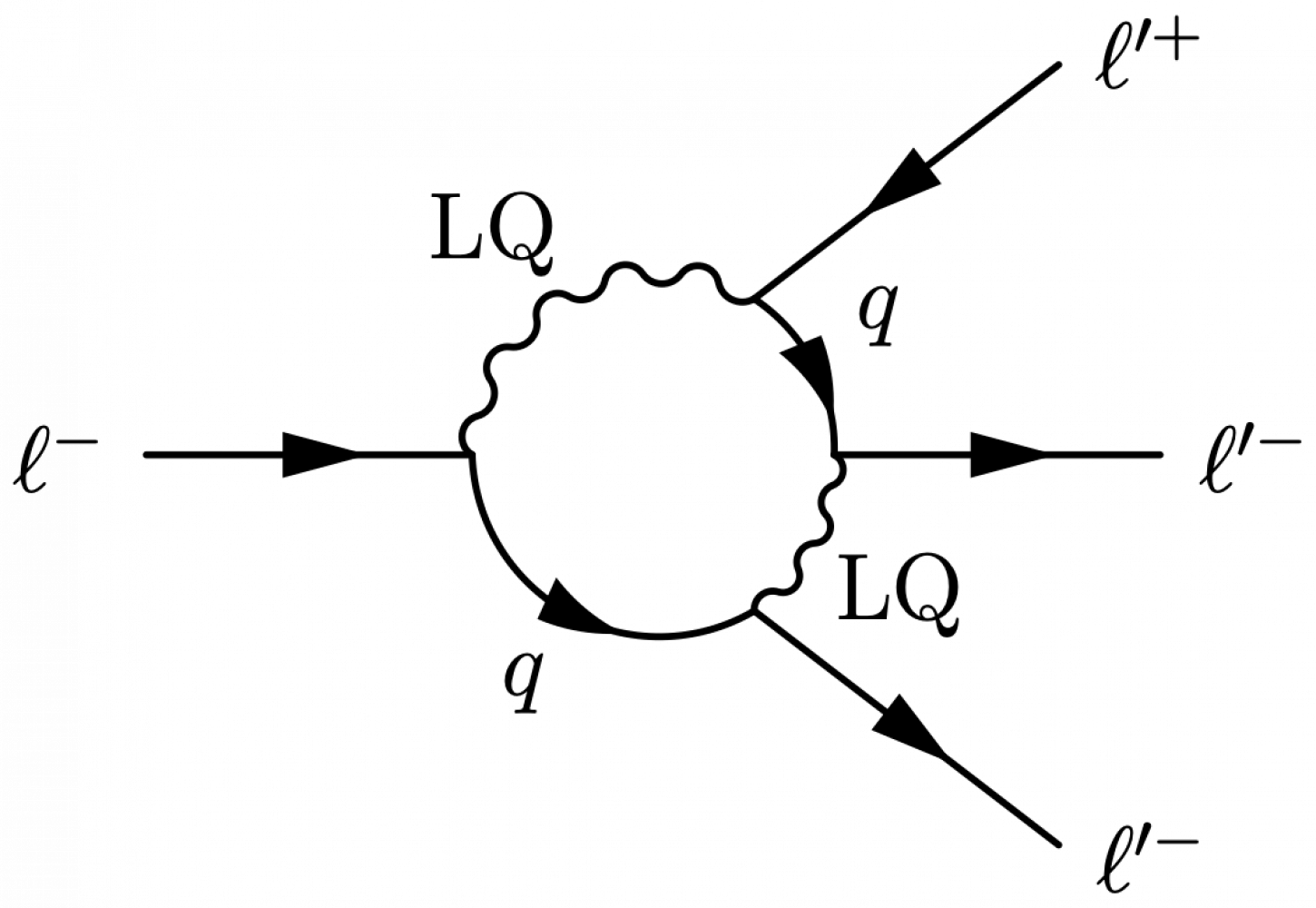
Leptoquark
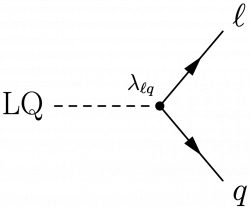
Here are some examples of processes with leptoquarks.
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(100,80) \fmfleft{LQ} \fmfright{q,l} \fmf{dashes,l.s=left,t=1.2}{LQ,v} \fmf{fermion}{v,q} \fmf{fermion}{v,l} \fmfv{l=LQ}{LQ} \fmfv{l.a=-28,l=$q$}{q} \fmfv{l.a=28,l=$\ell$}{l} \fmfdot{v} \fmfv{l.a=115,l=\large$\lambda_{\ell q}$}{v} \end{fmfgraph*} \end{fmffile}
Pair production
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,120) \fmfstraight \fmfleft{i2,g2,d,g1,i1} \fmfright{o4,o3,o2,o1} \fmftop{top} \fmfbottom{bot} % gluonS \fmf{gluon,tension=1.4}{v,g1} \fmf{gluon,tension=1.4}{g2,v} \fmf{gluon,tension=1.6}{v,h} \fmf{dashes,tension=1.2,label=LQ,l.s=right}{v1,h} \fmf{dashes,tension=1.2,label=$\overline{\text{LQ}}$,l.s=right}{h,v2} % decay products \fmf{phantom,tension=0.8}{top,v1} \fmf{phantom,tension=0.8}{v2,bot} \fmfshift{16 down}{o1} \fmfshift{ 8 down}{o2} \fmfshift{ 8 up}{o3} \fmfshift{16 up}{o4} \fmf{fermion,tension=1.8}{o1,v1,o2} \fmf{fermion,tension=1.8}{o4,v2,o3} % labels \fmflabel{$g$}{g1} \fmflabel{$g$}{g2} \fmflabel{$\overline{\ell}$}{o1} \fmflabel{$q$}{o2} \fmflabel{$\ell$}{o3} \fmflabel{$\overline{q}$}{o4} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(100,120) \fmfstraight \fmfleft{i2,g,i1} \fmfright{o4,o3,o2,o1} \fmftop{top} \fmfbottom{bot} % gluonS \fmf{gluon,tension=1.6}{g,h} \fmf{dashes,tension=1.3,label=LQ,l.s=right}{v1,h} \fmf{dashes,tension=1.3,label=$\overline{\text{LQ}}$,l.s=right}{h,v2} % decay products \fmf{phantom,tension=1.0}{top,v1} \fmf{phantom,tension=1.0}{v2,bot} \fmfshift{16 down}{o1} \fmfshift{ 8 down}{o2} \fmfshift{ 8 up}{o3} \fmfshift{16 up}{o4} \fmf{fermion,tension=1.8}{o1,v1,o2} \fmf{fermion,tension=1.8}{o4,v2,o3} % labels \fmflabel{$g$}{g} \fmflabel{$\tau^+$}{o1} \fmflabel{b}{o2} \fmflabel{\vspace{8pt}$\tau^-$}{o3} \fmflabel{$\overline{\text{b}}$}{o4} \end{fmfgraph*} \end{fmffile}
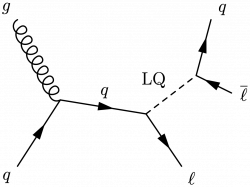
Single production
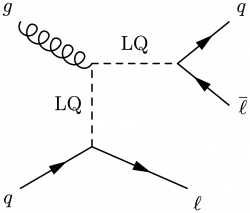
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(140,100) \fmfleft{i2,i1} \fmfright{o2,l2,l1} % gluon + quarks \fmf{gluon}{i1,v1} \fmf{fermion}{i2,v1} \fmf{fermion,label=$q$,label.side=left}{v1,v2} \fmf{fermion}{v2,o2} \fmflabel{$g$}{i1} \fmflabel{$q$}{i2} \fmflabel{$\ell$}{o2} % LQ \fmf{dashes,label=LQ,label.side=left}{v2,LQ} % LQ -> lepton + quark \fmf{fermion}{l2,LQ,l1} \fmfshift{20 right}{l1,l2} \fmflabel{$q$}{l1} \fmflabel{$\overline{\ell}$}{l2} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,100) \fmfstraight \fmfleft{i2,m,i1} \fmfright{o2,l2,l1} % skeleton \fmf{phantom,tension=1.0}{i1,v1} \fmf{phantom,tension=1.0}{v2,l1} \fmf{phantom,tension=1.5}{v1,v2} \fmf{phantom,tension=1.0}{i2,v1} \fmf{phantom,tension=1.0}{v2,o2} \fmf{phantom,tension=0.6}{i1,t1,m} \fmf{phantom,tension=0.6}{t1,LQ} \fmf{phantom,tension=2.0}{l1,LQ,l2} \fmffreeze % gluon + quarks \fmf{phantom,tension=5.0}{i1,g} % shorten leg \fmf{phantom,tension=5.0}{i2,q} % shorten leg \fmf{phantom,tension=5.0}{o2,l} % shorten leg \fmf{gluon}{g,v1} \fmf{fermion}{q,v1} \fmf{fermion,label=$q$,label.side=right}{v1,v2} \fmf{fermion}{v2,l} \fmflabel{$g$}{g} \fmflabel{$q$}{q} \fmflabel{$\ell$}{l} % LQ \fmf{dashes,tension=1.2,label=LQ,label.side=left}{v2,LQ} % LQ -> lepton + quark \fmf{fermion}{l2,LQ,l1} \fmfshift{20 right}{l1,l2} \fmflabel{$q$}{l1} \fmflabel{$\overline{\ell}$}{l2} \end{fmfgraph*} \end{fmffile}
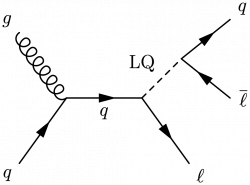
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(140,100) \fmfleft{i2,i1} \fmfright{o2,l2,l1} % gluon + quarks \fmf{gluon}{i1,v1} \fmf{fermion}{i2,v2,o2} \fmflabel{$g$}{i1} \fmflabel{$q$}{i2} \fmflabel{$\ell$}{o2} % LQs \fmf{dashes,label=LQ,label.side=left}{v2,v1,LQ} % LQ -> lepton + quark \fmf{fermion}{l2,LQ,l1} \fmflabel{$q$}{l1} \fmflabel{$\overline{\ell}$}{l2} \end{fmfgraph*} \end{fmffile}
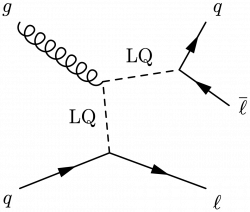
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,100) \fmfstraight \fmfleft{i2,i1} \fmfright{o2,l2,l1} % skeleton \fmf{phantom,tension=1.8}{i1,v1} \fmf{phantom,tension=1.0}{v1,l1} \fmf{phantom,tension=1.4}{v1,v2} \fmf{phantom,tension=1.8}{i2,v2} \fmf{phantom,tension=1.0}{v2,o2} \fmffreeze % gluon + quarks \fmf{gluon}{i1,v1} \fmf{fermion}{i2,v2,o2} \fmflabel{$g$}{i1} \fmflabel{$q$}{i2} \fmflabel{$\ell$}{o2} % LQs \fmf{dashes,tension=1.2,label=LQ,label.side=left}{v1,LQ} \fmf{dashes,label=LQ,label.side=left}{v2,v1} % LQ -> lepton + quark \fmf{fermion}{l2,LQ,l1} \fmfshift{5 right}{l1,l2} \fmfshift{20 left}{o2} \fmflabel{$q$}{l1} \fmflabel{$\overline{\ell}$}{l2} \end{fmfgraph*} \end{fmffile}
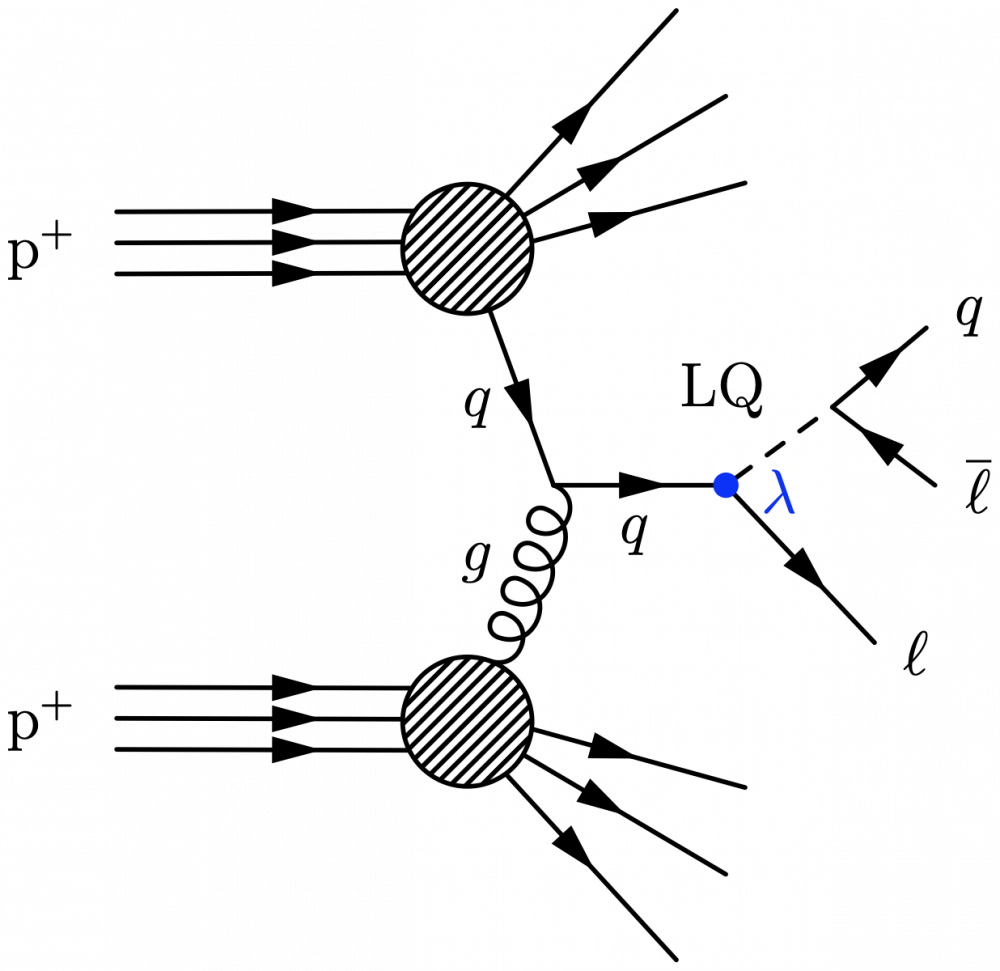
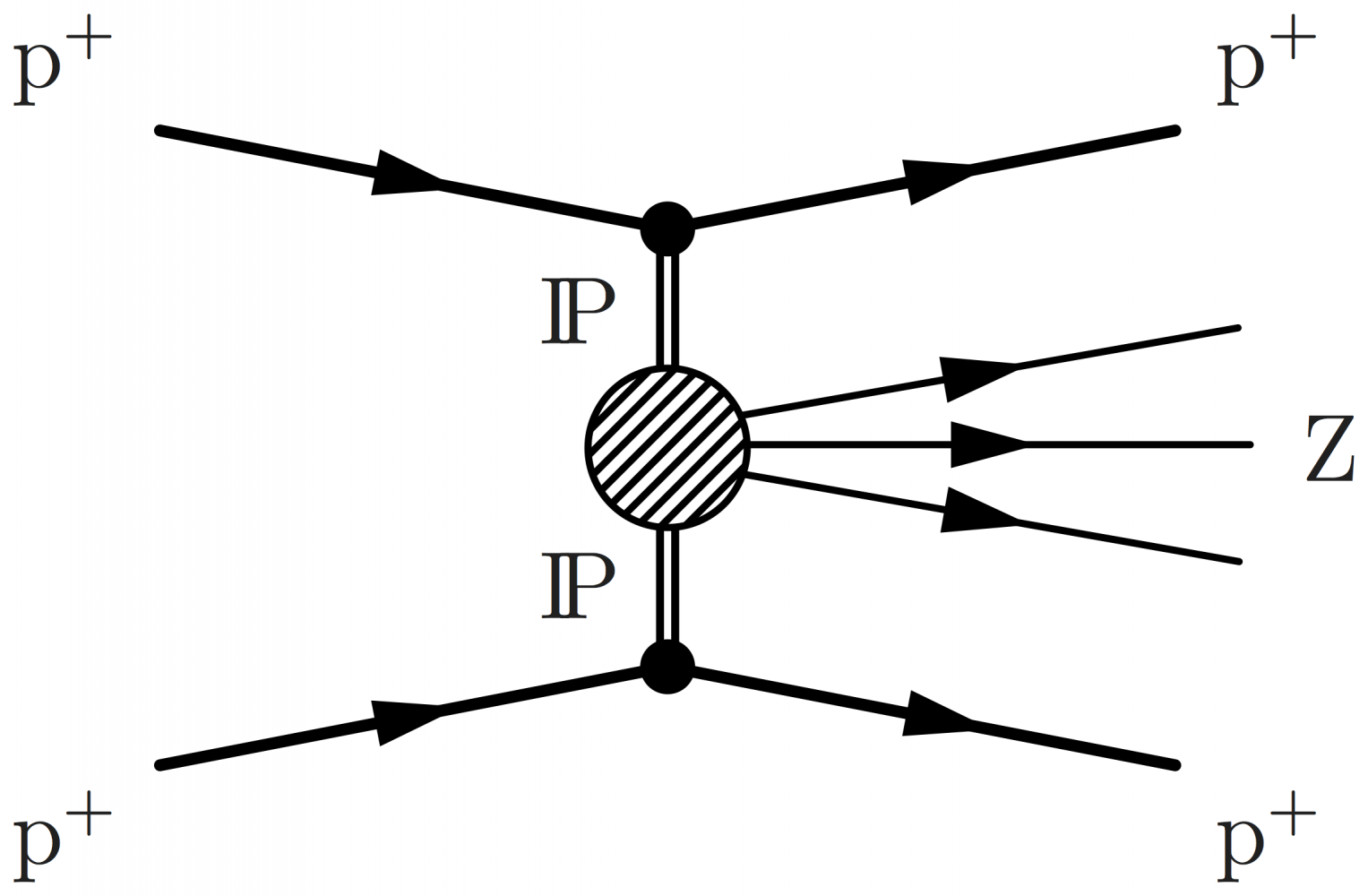
% preamble \usepackage{xcolor} \definecolor{myblue}{rgb}{.0,.13,.98} % 0,32,250 % body \large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,180) \fmfleft{i1,iq,i2,ip,i3} \fmfright{y1,y2,y3,d,o1,o2,f1,o3,f2,d,x3,x2,x1} \fmfset{arrow_len}{10} % skeleton \fmf{phantom,t=0.48}{vq,vp} \fmf{phantom}{ip,vp,x1} \fmf{phantom}{iq,vq,y1} \fmffreeze \fmf{phantom,t=1.8}{vq,v1,vp} \fmf{phantom,t=1.8}{v1,v2} \fmf{phantom,t=1}{o3,v2,o2} \fmffreeze % partons \fmf{fermion,lab=$q$,l.s=right}{vp,v1} \fmf{gluon,lab=$g$,l.s=left}{vq,v1} % hard process \fmf{fermion,lab=$q$,l.s=right}{v1,v2} \fmf{fermion}{v2,o1} \fmfshift{10 right}{f1,f2} \fmf{dashes,t=2,lab=LQ,l.s=left}{v2,vf} \fmf{phantom,t=0.4}{x1,vf} % pull vf \fmf{fermion,t=1.4}{f1,vf,f2} % proton 1 \fmf{phantom}{ip,vp} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4,-6)} % proton 2 \fmf{phantom}{iq,vq} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4,-6)} % X \fmfshift{25 left}{x1} \fmfshift{20 left}{x2,x3} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.0 shifted (0.0, 2.0)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.0 shifted (0.0, 0.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 1.0 shifted (0.0,-2.0)} \fmfblob{25}{vp} % outgoing proton \fmfshift{25 left}{y1} \fmfshift{20 left}{y2,y3} \fmf{phantom}{vq,y1} % to help \fmfi \fmf{phantom}{vq,y2} % to help \fmfi \fmf{phantom}{vq,y3} % to help \fmfi \fmfi{fermion}{vpath (__vq,__y1) scaled 1.0 shifted (0.0,-2.0)} \fmfi{fermion}{vpath (__vq,__y2) scaled 1.0 shifted (0.0, 0.0)} \fmfi{fermion}{vpath (__vq,__y3) scaled 1.0 shifted (0.0, 2.0)} \fmfblob{25}{vq} % labels \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{ip} \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{iq} \fmfv{l=$\overline{\ell}$}{f1} \fmfv{l=$q$}{f2} \fmfv{l=$\ell$,l.a=-20}{o1} \fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=(.0,,.13,,.98), l=$\color{myblue}\lambda$,l.d=7,l.a=-10}{v2} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,90) \fmfstraight \fmfleft{i2,i1} \fmfright{o2,l2,l1} % skeleton \fmf{phantom,tension=1.8}{i1,v1} \fmf{phantom,tension=1.1}{v1,l1} \fmf{phantom,tension=1.6}{v1,v2} \fmf{phantom,tension=1.8}{i2,v2} \fmf{phantom,tension=1.1}{v2,o2} \fmffreeze % gluon + quarks \fmf{fermion}{i1,v1} \fmf{photon}{i2,v2} \fmf{fermion}{v2,o2} % LQs \fmf{dashes,tension=1.2,label=LQ,label.side=left}{v1,LQ} \fmf{fermion}{v1,v2} % LQ -> lepton + quark \fmf{fermion}{l2,LQ,l1} \fmfshift{5 right}{l1,l2} \fmfshift{2 down}{l2} \fmfshift{20 left}{o2} \fmfv{l.a=160,l=$q$}{i1} \fmfv{l.a=-165,l=$\gamma$}{i2} \fmfv{l.a=-20,l=$\ell$}{o2} \fmfv{l.a=20,l=$\overline{q}$}{l1} \fmfv{l.a=-10,l=$\overline{\ell}$}{l2} \fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=(.0,,.13,,.98), l=$\color{myblue}\lambda$,l.d=6,l.a=-45}{v1} \end{fmfgraph*} \end{fmffile}
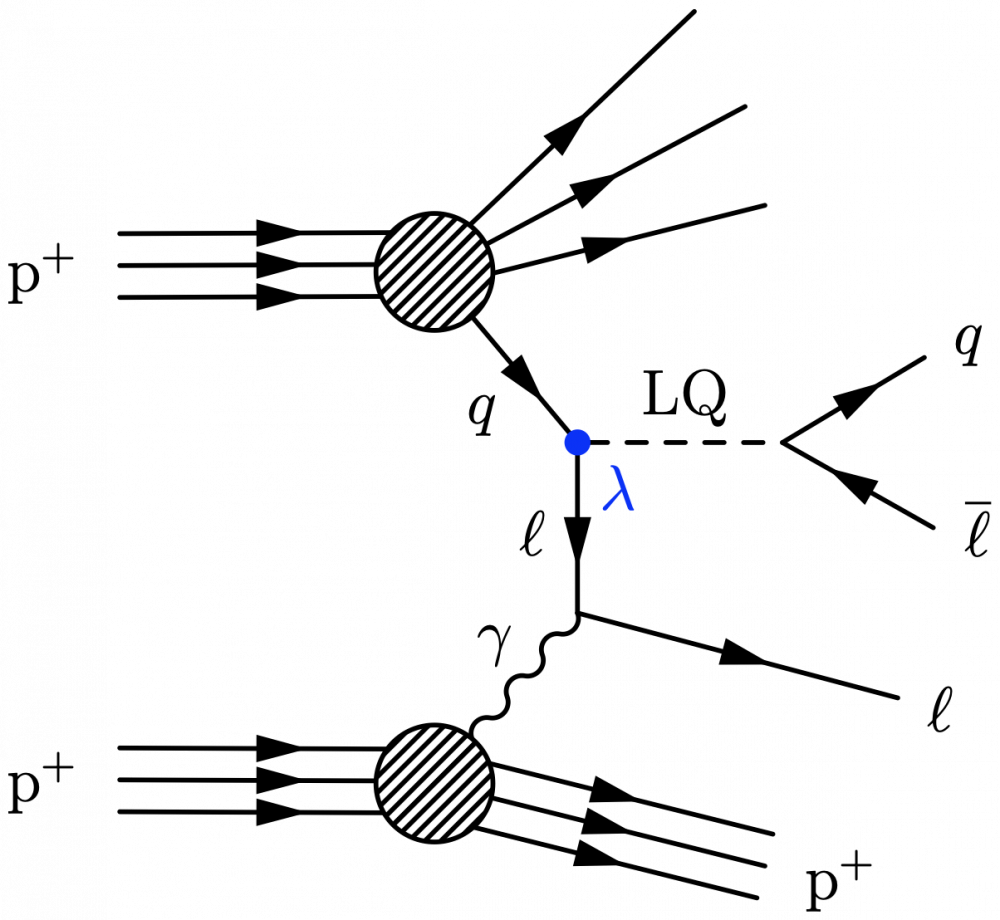
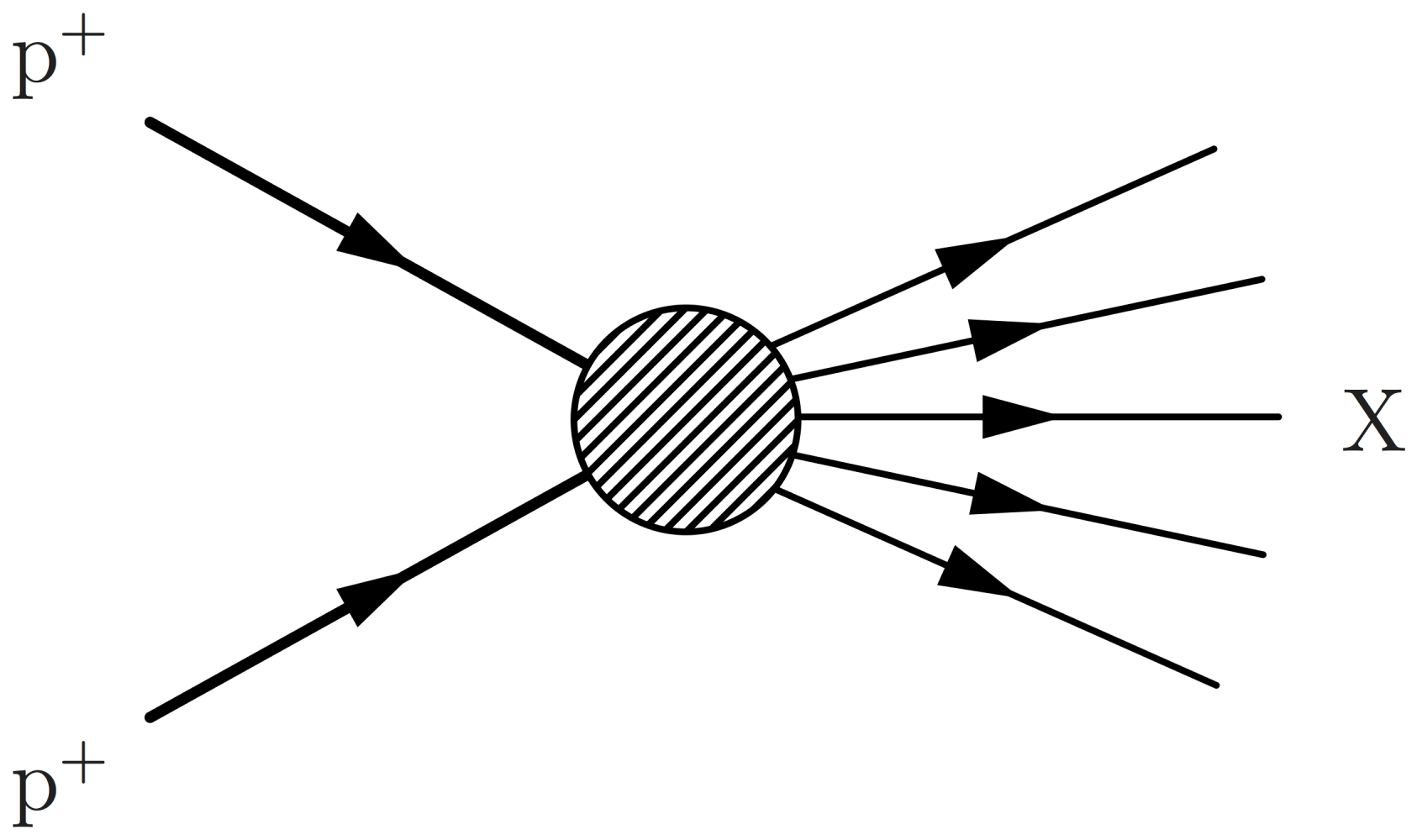
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,190) \fmfleft{i1,iq,i2,ip,i3} \fmfright{y1,y2,y3,d,o1,o2,f1,o3,f2,d,x3,x2,x1} \fmfset{arrow_len}{10} % skeleton \fmf{phantom,t=0.48}{vq,vp} \fmf{phantom,t=1.3}{ip,vp} \fmf{phantom,t=1.3}{iq,vq} \fmf{phantom}{vp,x1} \fmf{phantom}{vq,y1} \fmffreeze \fmf{phantom,t=1.6}{vq,v2,v1,vp} \fmf{phantom,t=0.7}{v1,o3} \fmf{phantom,t=0.7}{v2,o2} \fmffreeze % parton \fmf{fermion,t=1.6,lab=$q$}{vp,v1} \fmf{photon,t=1.6,lab=$\gamma$,l.d=3,l.s=left}{vq,v2} \fmf{fermion,t=1,lab=$\ell$,l.s=right}{v1,v2} \fmf{fermion,t=1}{v2,o1} % hard process \fmfshift{5 right}{f1,f2} \fmf{dashes,t=2,lab=LQ,l.d=3,l.s=left}{v1,vf} \fmf{fermion,t=1.4}{f1,vf,f2} %\fmf{fermion,t=1}{v2,o1} % proton 1 \fmf{phantom}{ip,vp} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4,-6)} % proton 2 \fmf{phantom}{iq,vq} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4,-6)} % X \fmfshift{25 left}{x1} \fmfshift{20 left}{x2,x3} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.0 shifted ( 0.0, 2.5)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.0 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 1.0 shifted ( 0.0,-3.0)} \fmfblob{22}{vp} % outgoing proton \fmfshift{25 left}{y1} \fmfshift{20 left}{y2,y3} \fmf{phantom}{vq,y1} % to help \fmfi \fmf{phantom}{vq,y2} % to help \fmfi \fmf{phantom}{vq,y3} % to help \fmfi \fmfi{fermion}{vpath (__vq,__y3) scaled 1.0 shifted (-1.5,-6.0)} \fmfi{fermion}{vpath (__vq,__y3) scaled 1.0 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vq,__y3) scaled 1.0 shifted ( 1.5, 6.0)} \fmfblob{22}{vq} % labels \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{ip} \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{iq} \fmfv{l=$\text{p}^+$,l.a=-20,l.d=8}{y3} \fmfv{l=$\overline{\ell}$}{f1} \fmfv{l=$q$}{f2} \fmfv{l=$\ell$,l.a=-20}{o1} \fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=(.0,,.13,,.98), l=$\color{myblue}\lambda$,l.d=6,l.a=-45}{v1} \end{fmfgraph*} \end{fmffile}
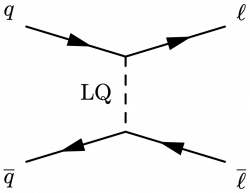
Nonresonant (t-channel) production
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,60) \fmfleft{i2,i1} \fmfright{o2,o1} \fmf{fermion}{i1,v1,o1} \fmf{fermion}{o2,v2,i2} \fmf{dashes,label=LQ,l.s=right,t=0.8}{v1,v2} \fmfv{l.a=150,l=$q$}{i1} \fmfv{l.a=30,l=$\ell$}{o1} \fmfv{l.a=-150,l=$\overline{q}$}{i2} \fmfv{l.a=-30,l=$\overline{\ell}$}{o2} \end{fmfgraph*} \end{fmffile}
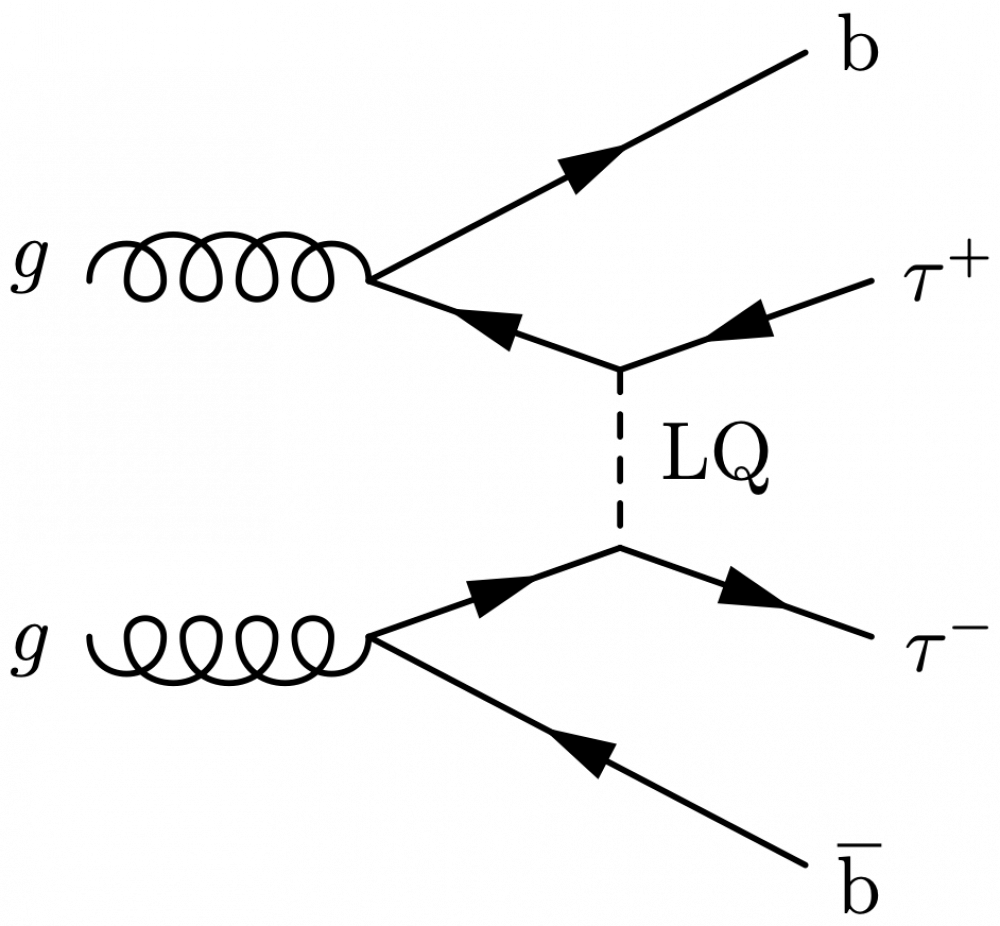
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,120) \fmfleft{d,d,g2,d,d,g1,d,d} \fmfright{b2,d,t2,d,d,t1,d,b1} % gluons \fmf{gluon,tension=1.8}{v1,g1} \fmf{gluon,tension=1.8}{g2,v2} \fmf{phantom}{v1,t1} \fmf{phantom}{v2,t2} \fmffreeze % b quarks \fmf{fermion}{b2,v2,vl2} \fmf{fermion}{vl1,v1,b1} % LQ (t-channel) \fmf{dashes,tension=1,label=LQ,l.s=left}{vl1,vl2} % tau leptons \fmf{fermion}{t1,vl1} \fmf{fermion}{vl2,t2} % labels \fmfv{l=$g$,l.a=160,l.d=6}{g1} \fmfv{l=$g$,l.a=-160,l.d=6}{g2} \fmfv{l=b,l.a=20,l.d=5}{b1} \fmfv{l=$\overline{\text{b}}$,l.a=-20,l.d=5}{b2} \fmfv{l=$\tau^+$,l.a=20,l.d=5}{t1} \fmfv{l=$\tau^-$,l.a=-5,l.d=5}{t2} \end{fmfgraph*} \end{fmffile}
Z' and W'
Here are some examples of processes with Z' and W'.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,60) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmf{fermion}{i1,v1,o1} \fmffreeze \fmf{fermion,tension=1.5}{o3,v3,o2} \fmf{phantom,tension=1.8}{i3,v3} \fmflabel{b}{i1} \fmflabel{c}{o1} \fmflabel{$\tau$}{o2} \fmflabel{$\nu_\tau$}{o3} % boson \fmf{boson,label=W$'$,label.side=left}{v3,v1} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,60) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmf{fermion}{i1,v1,o1} \fmffreeze \fmf{fermion,tension=1.5}{o3,v3,o2} \fmf{phantom,tension=1.8}{i3,v3} \fmflabel{b}{i1} \fmflabel{s}{o1} \fmflabel{$\mu$}{o2} \fmflabel{$\mu$}{o3} % boson \fmf{boson,label=Z$'$,label.side=left}{v3,v1} \fmfblob{16}{v1} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(110,100) \fmfleft{i2,i1} \fmfright{o2,m2,m1,o1} \fmfshift{30 right}{m1,m2} \fmf{fermion}{i1,v1,i2} \fmf{phantom}{o2,v2,o1} \fmf{boson,label=$\text{Z}/\gamma^*$,label.side=right}{v1,v2} \fmffreeze \fmf{fermion}{o2,v2,z,o1} \fmffreeze \fmf{boson,label=$\text{Z}'$,label.side=left}{z,m} \fmf{fermion,tension=1.4}{m2,m,m1} \fmf{phantom,tension=0.6}{i2,m} \fmflabel{$\mu^-$}{m1} \fmflabel{$\mu^+$}{m2} \fmflabel{$\mu^-$}{o1} \fmflabel{$\mu^+$}{o2} \fmflabel{$q$}{i1} \fmflabel{$\overline{q}'$}{i2} \end{fmfgraph*} \end{fmffile}
SUSY
More SUSY diagram are available here (images and here (GitHub).
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(80,120) %\fmfstraight \fmfleft{i2,b,i1} \fmfright{o4,o3,o2,o1} \fmftop{top} \fmfbottom{bot} % blob \fmfblob{16}{b} \fmf{dashes,tension=1.3,label=$\tilde{\text{t}}$,l.s=right}{v1,b} \fmf{dashes,tension=1.3,label=$\overline{\tilde{\text{t}}}$,l.s=right}{b,v2} % decay products %\fmf{phantom,tension=1.0}{top,v1} %\fmf{phantom,tension=1.0}{v2,bot} \fmfshift{16 down}{o1} \fmfshift{ 8 down}{o2} \fmfshift{ 8 up}{o3} \fmfshift{16 up}{o4} \fmf{dots,tension=1.8}{v1,o1} \fmf{fermion,tension=1.8}{o2,v1} \fmf{fermion,tension=1.8}{v2,o4} \fmf{dots,tension=1.8}{o3,v2} % labels \fmflabel{$\tilde{\chi}_1^0$}{o1} \fmflabel{$\overline{\text{t}}$}{o2} \fmflabel{$\tilde{\chi}_1^0$}{o3} \fmflabel{t}{o4} \end{fmfgraph*} \end{fmffile}
Top quark pair decay into a W boson pair and a b quark pair
A top quark pair decaying in to bbWW with the W boson pair in the semi-leptonic final state.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(180,150) \fmfset{arrow_len}{3.5mm} \fmfstraight \fmfleft{i1,i2,i3,i4,i5} \fmfright{o1,o2,o3,o4,o5,o6} % bW -> bqq \fmf{boson,tension=1.5,label={$\text{W}^+$},label.side=right}{v2,v21} % W boson \fmf{fermion}{v2,o6} % b quark \fmf{fermion}{o5,v21,o4} % bW -> blnu \fmf{boson,tension=1.5,label={$\text{W}^-$},label.side=right}{v1,v11} % W boson \fmf{fermion}{v1,o3} % b quark \fmf{fermion}{o1,v11,o2} \fmf{fermion,tension=1.5}{v1,i3,v2} % top quark pair \fmf{phantom,label={$\bar{\text{t}}$},tension=1}{i3,v1} \fmf{phantom,label={$\text{t}$},tension=1}{i3,v2} \fmflabel{\makebox[3.2mm][l]{$\bar{\nu}_\ell$} /\, q}{o1} \fmflabel{\makebox[3.2mm][l]{$\ell^-$} /\, $\bar{\text{q}}'$}{o2} \fmflabel{$\bar{\text{b}}$}{o3} \fmflabel{\makebox[3.2mm][l]{$\bar{\text{q}}'$} /\, $\nu_\text{l}$}{o4} \fmflabel{\makebox[3.2mm][l]{q} /\, $\ell^+$}{o5} \fmflabel{$\text{b}$}{o6} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(180,150) \fmfset{arrow_len}{3.5mm} \fmfstraight \fmfleft{i1,i2,i3,i4,i5} \fmfright{o1,o2,o3,o4,o5,o6} % qq -> g \fmf{fermion,tension=1.5}{i4,vg,i2} \fmf{gluon,tension=1.5}{vtt,vg} \fmf{phantom,tension=0.5}{o3,vtt,o4} % balance \fmflabel{$\bar{q}$}{i2} \fmflabel{$q$}{i4} \fmffreeze % tt \fmf{fermion,tension=1.2}{v1,vtt,v2} % top quark pair \fmf{phantom,label={$\bar{\text{t}}$},tension=0,label.side=right}{vtt,v1} % top label \fmf{phantom,label={$\text{t}$},tension=0,label.side=left}{vtt,v2} % top label \fmf{phantom,tension=1}{o1,v1,o2} % balance \fmf{phantom,tension=1}{o5,v2,o6} % balance \fmf{phantom,tension=0.5}{i1,v1,v2,i5} % balance \fmffreeze % bW -> bqq \fmf{boson,tension=0.8,label={$\text{W}^+$},label.side=right}{v2,v21} % W boson \fmf{fermion,tension=1.2}{v2,o6} % b quark \fmf{fermion}{o5,v21,o4} % bW -> blnu \fmf{boson,tension=1.4,label={$\text{W}^-$},label.side=right}{v1,v11} % W boson \fmf{fermion,tension=0.5}{v1,o3} % b quark \fmf{fermion}{o1,v11,o2} \fmflabel{\makebox[3.2mm][l]{$\bar{\nu}_\ell$} /\, q}{o1} \fmflabel{\makebox[3.2mm][l]{$\ell^-$} /\, $\bar{\text{q}}'$}{o2} \fmflabel{$\bar{\text{b}}$}{o3} \fmflabel{\makebox[3.2mm][l]{$\bar{\text{q}}'$} /\, $\nu_\ell$}{o4} \fmflabel{\makebox[3.2mm][l]{q} /\, $\ell^+$}{o5} \fmflabel{$\text{b}$}{o6} \end{fmfgraph*} \end{fmffile}
Higgs boson pair decay into a W boson pair and a b quark pair
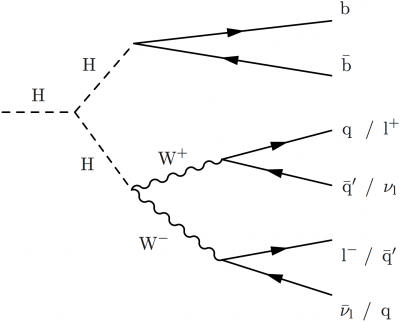
A Higgs pair decaying into bbWW with the W boson pair in the semi-leptonic final state.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(180,150) \fmfset{arrow_len}{3.5mm} \fmfstraight \fmfleft{i1,i2,i3,i4} \fmfright{o1,o2,o3,o4,o5,o6} % WW -> qqlnu \fmf{fermion}{o1,v11,o2} % lepton, neutrino \fmf{fermion}{o3,v12,o4} % quarks \fmf{phantom}{i1,v11} \fmf{phantom}{i3,v12} \fmf{phantom,tension=0.5}{v11,v12} \fmffreeze % H -> bb \fmf{fermion}{o5,v2,o6} % b quark \fmf{phantom,tension=1.4}{i2,v1} \fmf{phantom,tension=3}{i4,v2} \fmf{phantom,tension=0.4}{v1,v2} % H -> WW \fmf{boson,label={$\text{W}^+$},label.side=left}{v1,v12} % W boson \fmf{boson,label={$\text{W}^-$},label.side=right}{v1,v11} % W boson \fmffreeze % Higgs bosons \fmf{dashes,label=H,label.side=left,tension=1.5}{i3,v0} % H boson \fmf{dashes,label=H,label.side=right,tension=1}{v0,v1} % H boson \fmf{dashes,label=H,label.side=left,tension=1}{v0,v2} % H boson \fmf{phantom,tension=0.1}{i4,v0} \fmflabel{\makebox[3.2mm][l]{$\bar{\nu}_\text{l}$} /\, q}{o1} \fmflabel{\makebox[3.2mm][l]{$\text{l}^-$} /\, $\bar{\text{q}}'$}{o2} \fmflabel{\makebox[3.2mm][l]{$\bar{\text{q}}'$} /\, $\nu_\text{l}$}{o3} \fmflabel{\makebox[3.2mm][l]{q} /\, $\text{l}^+$}{o4} \fmflabel{$\bar{\text{b}}$}{o5} \fmflabel{$\text{b}$}{o6} \end{fmfgraph*} \end{fmffile}
Note that \makebox is used to create boxes of the same width, such that the slashes are horizontally aligned.
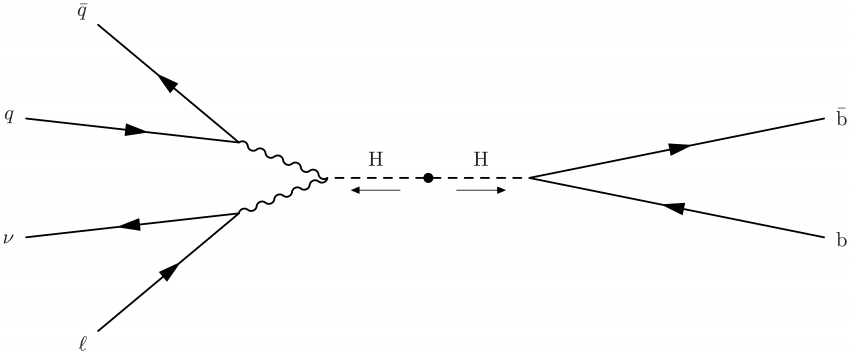
Naive sketch of the topology of Higgs pair production, where the Higgs bosons are boosted back to back:
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(400,150) \fmfset{wiggly_len}{10} \fmfset{arrow_len}{12} \fmfleft{i1,i2,i3,i4} \fmfright{o0,o1,o2,o3} \fmf{fermion}{i1,v1,i2} \fmf{fermion}{i3,v2,i4} \fmf{fermion,tension=1.2}{o1,z,o2} \fmf{boson,tension=4}{v1,w} \fmf{boson,tension=4}{v2,w} \fmfdot{p} \marrow{a}{down}{}{}{p,z} \marrow{b}{down}{}{}{p,w} \fmf{dashes,label={H},tension=7}{p,w} \fmf{dashes,label={H},label.side=left,tension=7}{p,z} \fmflabel{$\ell$}{i1} \fmflabel{$\nu$}{i2} \fmflabel{$q$}{i3} \fmflabel{$\bar{q}$}{i4} \fmflabel{b}{o1} \fmflabel{$\bar{\text{b}}$}{o2} \end{fmfgraph*} \end{fmffile}
where \marrow is predefined in the preamble as few sections above.
Ditau resonance in association with jets
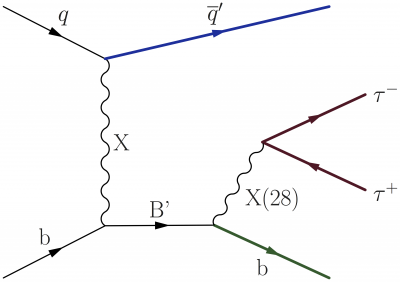
Tau pair resonance in association with two quarks, one of which is a b quark, in the t-channel, like single top production:
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(300,200) \fmfset{wiggly_len}{8mm} \fmfleft{i1,i2} \fmfright{o1,t1,t2,o2} \fmf{phantom,tension=1.2,label=b}{i1,v11} \fmf{phantom,tension=1.2}{i2,v12} \fmf{phantom,tension=1}{i1,v11,o1} \fmf{phantom,tension=1}{i2,v12,o2} \fmf{boson,tension=1,label=X}{v11,v12} \fmffreeze \fmf{fermion}{i1,v11,v21} \fmf{fermion,width=2,foreground=(0.070,,0.349,,0.156)}{v21,o1} \fmf{fermion,label=$q$}{i2,v12} \fmf{fermion,label=$\overline{q}'$,label.side=left,width=2,foreground=(0.035,,0.168,,0.623)}{v12,o2} \fmf{phantom,tension=2,label=B'}{v11,v21} \fmf{phantom,tension=1.8,label=b}{v21,o1} \fmf{boson,label=X(28)}{v21,t} \fmf{fermion,width=2,foreground=(0.349,,0.070,,0.125)}{t1,t,t2} \fmf{phantom,tension=1}{v12,t} \fmf{phantom,tension=0.4}{v12,v21} \fmflabel{$\tau^+$}{t1} \fmflabel{$\tau^-$}{t2} \end{fmfgraph*} \end{fmffile}
Higgs mass loop corrections with SUSY and VLQs
With \parbox{<width>pt} (with unit point pt) each Feynman diagram in a fmfgraph environment with also with width can be put in a box which centers vertically with the text line, so you can use diagrams in equations. Here is an example of diagrams in equation between text in a LaTeX file.
Here are some examples of the hierarchy problem in terms of Higgs mass squared corrections using BSM contributions like those from SUSY and vector-like quarks (VLQs). \quad is used to achieve equal spacing.
\begin{fmffile}{feyngraph} \Delta m_H^2 = \quad\parbox{100pt}{ \begin{fmfgraph*}(100,80) \fmfleft{i} \fmfright{o} \fmfv{label=H,l.a=60}{i} \fmfv{label=H,l.a=120}{o} \fmf{dashes,tension=1}{i,v1} % ,label=H,label.side=left \fmf{dashes,tension=1}{v2,o} \fmf{fermion,left,tension=0.4,label=$\text{t}$}{v1,v2,v1} \end{fmfgraph*}} \quad + \quad\parbox{100pt}{ \begin{fmfgraph*}(100,80) \fmfleft{i} \fmfright{o} \fmftop{m} \fmfv{label=H,l.a=60}{i} \fmfv{label=H,l.a=120}{o} \fmflabel{$\widetilde{\text{t}}$}{m} \fmf{dashes,tension=1}{i,v1} \fmf{dashes,tension=1}{v1,o} \fmf{dashes,right,tension=0}{v1,m,v1} \end{fmfgraph*}} \quad + \quad\ldots \end{fmffile}
\begin{fmffile}{feyngraph} \Delta m_H^2 = \quad\parbox{100pt}{ \begin{fmfgraph*}(100,80) \fmfleft{i} \fmfright{o} \fmfv{label=H,l.a=60}{i} \fmfv{label=H,l.a=120}{o} \fmf{dashes,tension=1}{i,v1} % ,label=H,label.side=left \fmf{dashes,tension=1}{v2,o} \fmf{fermion,left,tension=0.4,label=$\text{t}$}{v1,v2,v1} \end{fmfgraph*}} \quad + \quad\parbox{100pt}{ \begin{fmfgraph*}(100,80) \fmfleft{i} \fmfright{o} \fmfv{label=H,l.a=60}{i} \fmfv{label=H,l.a=120}{o} \fmf{dashes,tension=1}{i,v1} % ,label=H,label.side=left \fmf{dashes,tension=1}{v2,o} \fmf{fermion,left,tension=0.4,label=$\text{t}$}{v2,v1} \fmf{fermion,left,tension=0.4,label=$\text{T}$}{v1,v2} \end{fmfgraph*}} \quad + \quad\ldots \end{fmffile}
\begin{fmffile}{feyngraph} \Delta m_H^2 = \quad\parbox{100pt}{ \begin{fmfgraph*}(100,80) \fmfleft{i} \fmfright{o} \fmfv{label=H,l.a=60}{i} \fmfv{label=H,l.a=120}{o} \fmf{dashes,tension=1}{i,v1} % ,label=H,label.side=left \fmf{dashes,tension=1}{v2,o} \fmf{fermion,left,tension=0.4,label=$\text{t}$}{v1,v2,v1} \end{fmfgraph*}} \quad + \quad\parbox{100pt}{ \begin{fmfgraph*}(100,80) \fmfleft{i} \fmfright{o} \fmfv{label=H,l.a=60}{i} \fmfv{label=H,l.a=120}{o} \fmf{dashes,tension=1}{i,v1} % ,label=H,label.side=left \fmf{dashes,tension=1}{v2,o} \fmf{fermion,left,tension=0.4,label=$\text{t}$}{v2,v1} \fmf{fermion,left,tension=0.4,label=$\text{T}$}{v1,v2} \end{fmfgraph*}} \quad + \quad\parbox{100pt}{ \begin{fmfgraph*}(100,80) \fmfleft{i} \fmfright{o} \fmftop{m} \fmfv{label=H,l.a=60}{i} \fmfv{label=H,l.a=120}{o} \fmflabel{$\text{T}$}{m} \fmf{dashes,tension=1}{i,v1} \fmf{dashes,tension=1}{v1,o} \fmf{fermion,right,tension=0}{v1,m,v1} \end{fmfgraph*}} \quad + \quad\ldots \end{fmffile}
Neutral kaon decay and mixing
With a user-defined command and the scalerel package, we can make curly braces of custom size (inspiration):
\usepackage{scalerel} \newcommand{\mylbrace}[2]{\vspace{#2pt}\hspace{6pt}\scaleleftright[\dimexpr5pt+#1\dimexpr0.06pt]{\lbrace}{\rule[\dimexpr2pt-#1\dimexpr0.5pt]{-4pt}{#1pt}}{.}} \newcommand{\myrbrace}[2]{\vspace{#2pt}\scaleleftright[\dimexpr5pt+#1\dimexpr0.06pt]{.}{\rule[\dimexpr2pt-#1\dimexpr0.5pt]{-4pt}{#1pt}}{\rbrace}\hspace{6pt}}
with two arguments: the vertical size and the vertical shift (with \vspace). Position can be further finetuned by using \fmfv's label distance (l.d) and angle (l.a) options
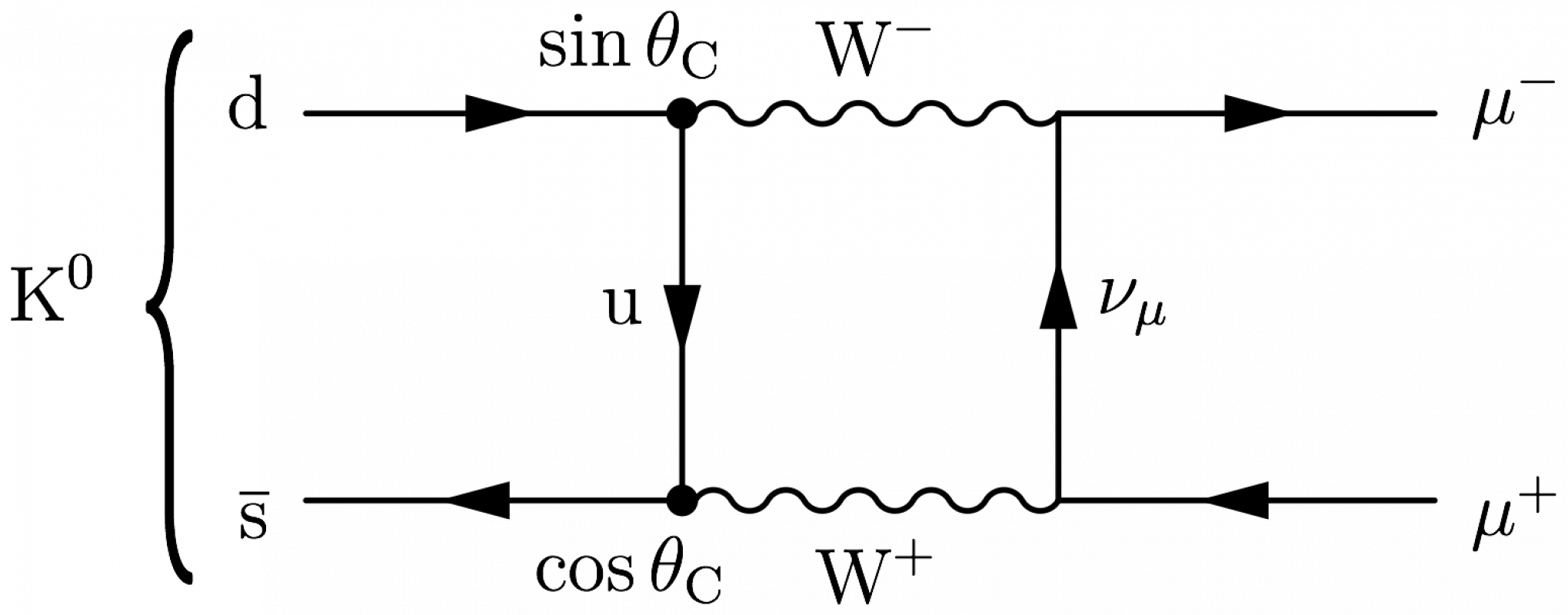
With above three lines added in the preamble, one can make for example neutral kaon decay (described by the GIM mechanism). Notice that a middle point K on the right was defined to serve as an anchor for \fmfv which contains the brace:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(175,60) \fmfstraight \fmfleft{i2,K,i1} \fmfright{o2,o1} % quarks \fmf{fermion}{i1,t1} \fmf{fermion}{t4,i2} \fmflabel{d}{i1} \fmflabel{$\overline{\text{s}}$}{i2} \fmfv{l.d=20,l.a=180,l={$\text{K}^0$\mylbrace{86}{0}}}{K} % placeholders quarks-muons \fmf{phantom,tension=1}{t1,t2} \fmf{phantom,tension=1}{t4,t3} % muons \fmf{fermion,tension=1}{t2,o1} \fmf{fermion,tension=1}{o2,t3} \fmflabel{$\mu^-$}{o1} \fmflabel{$\mu^+$}{o2} % box loop \fmf{boson,tension=0,label=$\text{W}^-$,label.side=left}{t1,t2} \fmf{boson,tension=0,label=$\text{W}^+$,label.side=left}{t3,t4} \fmf{fermion,tension=0,label=u}{t1,t4} \fmf{fermion,tension=0,label=$\nu_\mu$}{t3,t2} \fmfv{d.shape=circle,d.size=4,l=$\sin\theta_\text{C}\quad$,l.a=110}{t1} \fmfv{d.shape=circle,d.size=4,l=$\cos\theta_\text{C}\quad$,l.a=-110}{t4} \end{fmfgraph*} \end{fmffile}
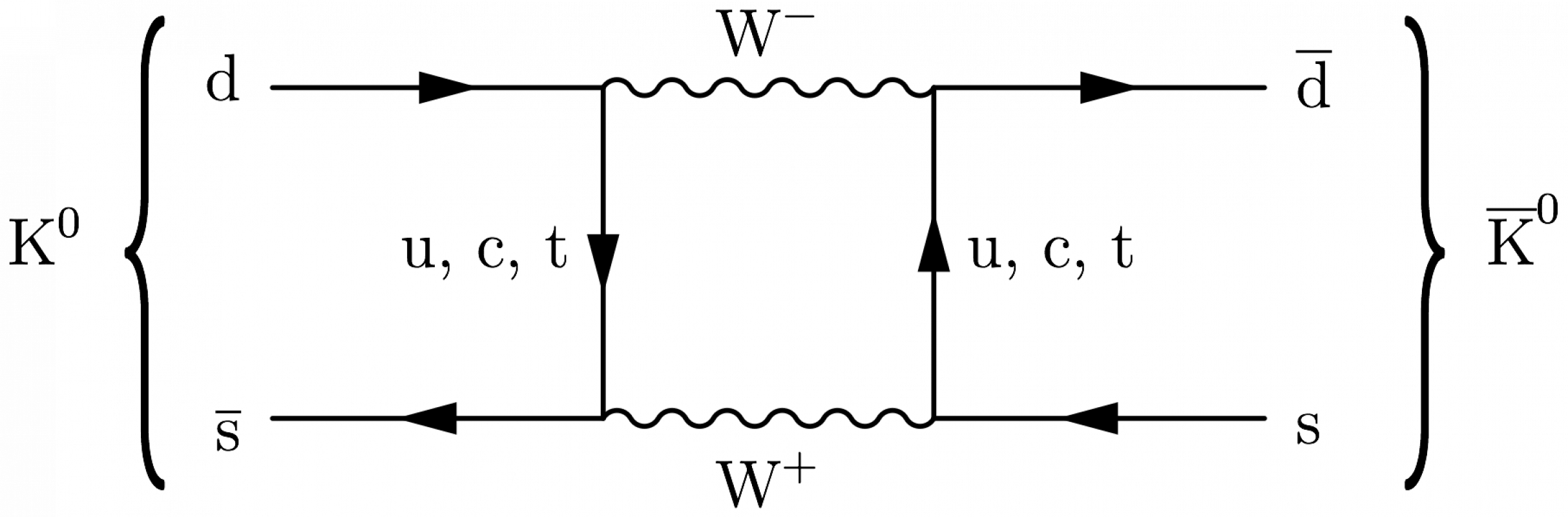
Or with neutral kaon mixing:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(180,60) \fmfstraight \fmfleft{i2,K,i1} \fmfright{o2,Kbar,o1} % quarks left \fmf{fermion}{i1,t1} \fmf{fermion}{t4,i2} \fmflabel{d}{i1} \fmflabel{$\overline{\text{s}}$}{i2} \fmfv{l.d=22,l.a=180,l={$\text{K}^0$\mylbrace{86}{0}}}{K} % placeholders between quarks \fmf{phantom,tension=1}{t1,t2} \fmf{phantom,tension=1}{t4,t3} % quarks \fmf{fermion,tension=1}{t2,o1} \fmf{fermion,tension=1}{o2,t3} \fmflabel{$\overline{\text{d}}$}{o1} \fmflabel{s}{o2} \fmfv{l.d=25,l.a=0,l={\myrbrace{86}{0}$\overline{\text{K}}^0$}}{Kbar} % box loop \fmf{boson,tension=0,label=$\text{W}^-$,label.side=left}{t1,t2} \fmf{boson,tension=0,label=$\text{W}^+$,label.side=left}{t3,t4} \fmf{fermion,tension=0,label=u,, c,, t}{t1,t4} \fmf{fermion,tension=0,label=u,, c,, t}{t3,t2} \end{fmfgraph*} \end{fmffile}
Notice that the use of double comma's is needed inside \fmf, to make clear that the string are not separate arguments.
Instead of a brace, one can also make a oval blob with the following lines in the preamble (source):
\begin{filecontents*}{vovalblob.mp} vardef vovalblob (expr bd, a) (text vl)= forsuffixes $=vl: if not vexists $: venter $; fi vlist[vlookup $]decor.shape := fullcircle xscaled a; vlist[vlookup $]decor.size := bd; vlist[vlookup $]decor.sty := "shaded"; endfor enddef; \end{filecontents*} \def\fmfovalblob#1#2#3{\fmfcmd{input vovalblob; vovalblob ((#1), (#2), \fmfpfx{#3});}}
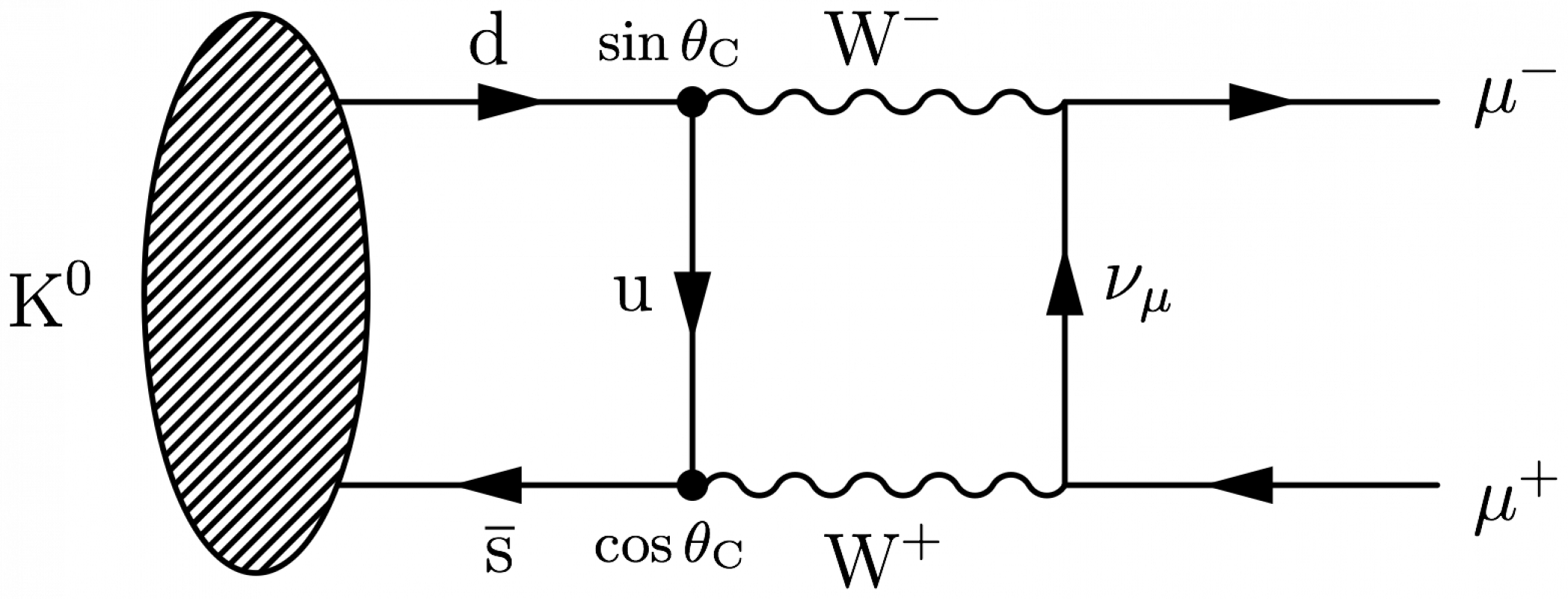
Here one defines the command \fmfovalblob with two arguments: one for the size and one for the eccentricity. Use it as:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(175,60) \fmfstraight \fmfleft{i2,K,i1} \fmfright{o2,o1} % quarks \fmf{fermion,label.side=left,label=d\;}{i1,t1} \fmf{fermion,label.side=left,label=$\overline{\text{s}}$}{t4,i2} \fmfshift{10 left}{K} \fmfovalblob{.5w}{.4}{K} \fmfv{l.d=25,l.a=180,l=$\text{K}^0$}{K} % placeholders quarks-muons \fmf{phantom,tension=1}{t1,t2} \fmf{phantom,tension=1}{t4,t3} % muons \fmf{fermion,tension=1}{t2,o1} \fmf{fermion,tension=1}{o2,t3} \fmflabel{$\mu^-$}{o1} \fmflabel{$\mu^+$}{o2} % box loop \fmf{boson,tension=0,label=$\text{W}^-$,label.side=left}{t1,t2} \fmf{boson,tension=0,label=$\text{W}^+$,label.side=left}{t3,t4} \fmf{fermion,tension=0,label=u}{t1,t4} \fmf{fermion,tension=0,label=$\nu_\mu$}{t3,t2} \fmfv{d.shape=circle,d.size=4,l={\small$\sin\theta_\text{C}$\;},l.a=110}{t1} \fmfv{d.shape=circle,d.size=4,l={\small$\cos\theta_\text{C}$\;},l.a=-110}{t4} \end{fmfgraph*} \end{fmffile}
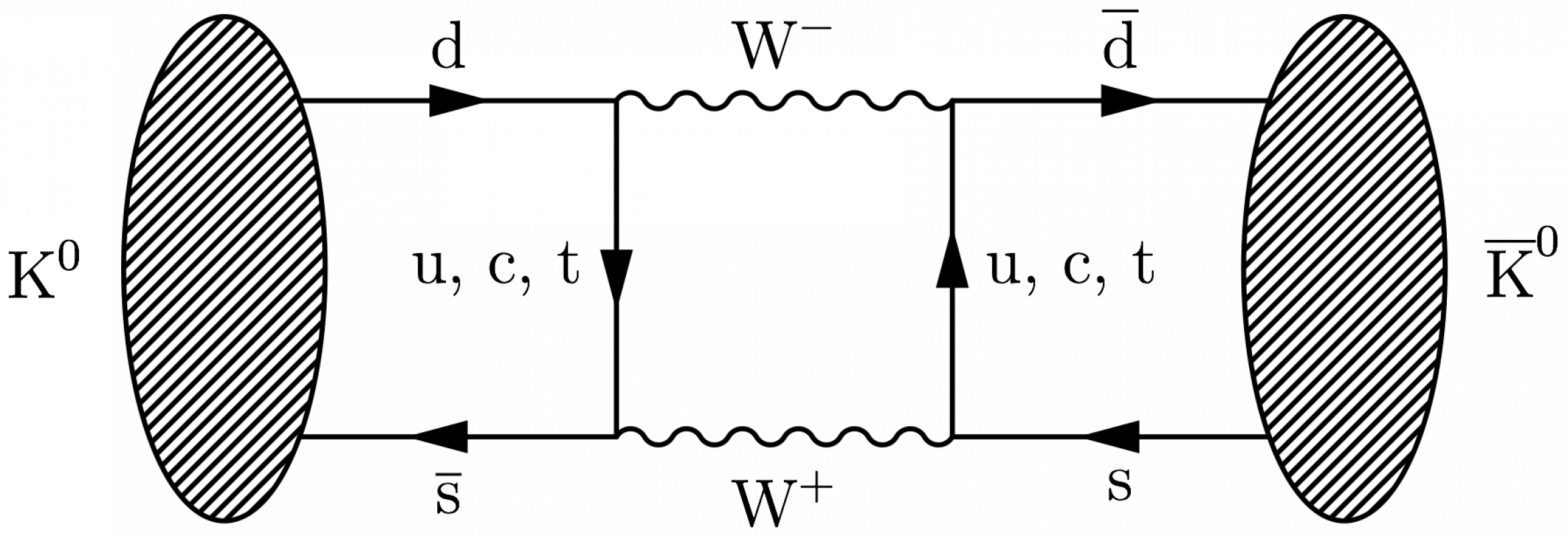
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(180,60) \fmfstraight \fmfleft{i2,K,i1} \fmfright{o2,Kbar,o1} % quarks left \fmf{fermion,label.side=left,label=d}{i1,t1} \fmf{fermion,label.side=left,label=$\overline{\text{s}}$}{t4,i2} \fmfshift{10 left}{K} \fmfovalblob{.5w}{.4}{K} \fmfv{l.d=25,l.a=180,l=$\text{K}^0$}{K} % placeholders between quarks \fmf{phantom,tension=1}{t1,t2} \fmf{phantom,tension=1}{t4,t3} % quarks right \fmf{fermion,tension=1,label.side=left,label=$\overline{\text{d}}$}{t2,o1} \fmf{fermion,tension=1,label.side=left,label=s}{o2,t3} \fmfshift{10 right}{Kbar} \fmfovalblob{.5w}{.4}{Kbar} \fmfv{l.d=25,l.a=3,l=$\overline{\text{K}}^0$}{Kbar} % box loop \fmf{boson,tension=0,label=$\text{W}^-$,label.side=left}{t1,t2} \fmf{boson,tension=0,label=$\text{W}^+$,label.side=left}{t3,t4} \fmf{fermion,tension=0,label=u,, c,, t}{t1,t4} \fmf{fermion,tension=0,label=u,, c,, t}{t3,t2} \end{fmfgraph*} \end{fmffile}
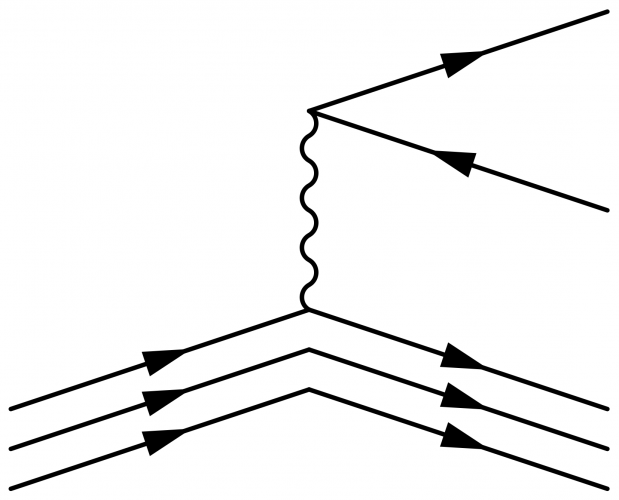
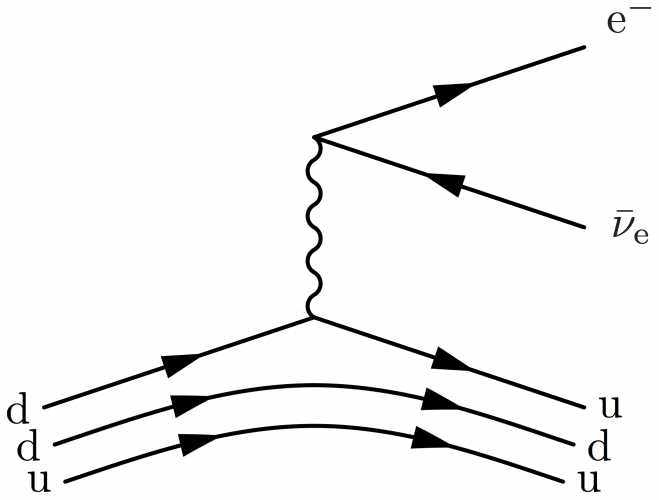
Neutron (beta) decay with spectator quarks
The \fmfi command is the “immediate mode” verion of \fmf. It allows to make lines that can be shifted and scaled with MetaPost syntax, so you can make multiple line representing a proton, for example elastic electron-proton scattering or neutron decay:
\begin{fmffile}{feyngraph} \begin{fmfgraph}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson}{v1,v3} % neutron \fmf{phantom}{i3,v3,o3} \fmffreeze \fmfi{fermion}{vpath (__i3,__v3) shifted ( 0, 0)} \fmfi{fermion}{vpath (__v3,__o3) shifted ( 0, 0)} \fmfi{fermion}{vpath (__i3,__v3) shifted ( 0,-8)} \fmfi{fermion}{vpath (__v3,__o3) shifted ( 0,-8)} \fmfi{fermion}{vpath (__i3,__v3) shifted ( 0,-16)} \fmfi{fermion}{vpath (__v3,__o3) shifted ( 0,-16)} \end{fmfgraph} \end{fmffile}
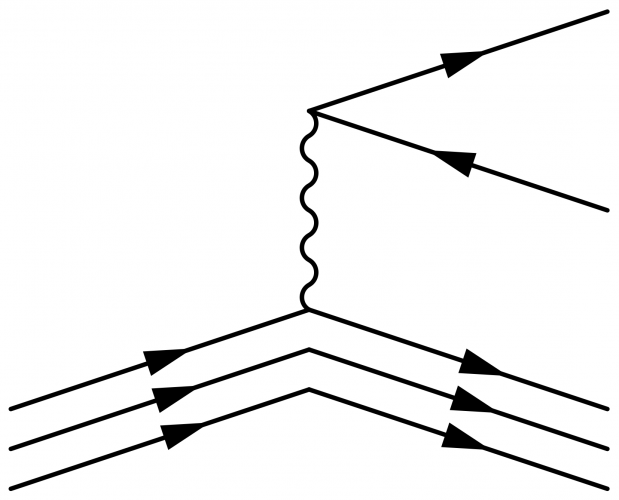
To gain more control over the quark lines and their arrows, put the following snippet in your preamble to define a new quark line:
\newcommand{\quark}[5]{ \fmfcmd{style_def quark#1 expr p = cdraw subpath (#2) of p shifted (#4); cfill (tarrow (p,(xpart(#2)+ypart(#2))*0.48*#3)) shifted (#4); enddef;} \fmf{quark#1,tension=0}{#5}}
It takes five arguments (#1–#5):
- unique label of the arrow object (containing only letters);
- two, comma-seperated values between
0and1, e.g.{0.1,0.9}, which allow you to shorten or lengthen either ends of the quark line; - value around
1to define the arrow head's position on the quark line; - two, comma-seperated values, e.g.
{1,-2}, to shift the line; - two or more, comma-seperated vertices.
\begin{fmffile}{feyngraph} \begin{fmfgraph}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson}{v1,v3} % neutron \fmf{phantom}{i3,v3,o3} \fmffreeze \quark{qai}{0.0,1.0}{0.94}{ 0, 0}{i3,v3} \quark{qbi}{0.0,1.0}{1.00}{ 0, -8}{i3,v3} \quark{qci}{0.0,1.0}{1.06}{ 0,-16}{i3,v3} \quark{qao}{0.0,1.0}{1.06}{ 0, 0}{v3,o3} \quark{qbo}{0.0,1.0}{1.00}{ 0, -8}{v3,o3} \quark{qco}{0.0,1.0}{0.94}{ 0,-16}{v3,o3} \end{fmfgraph} \end{fmffile}
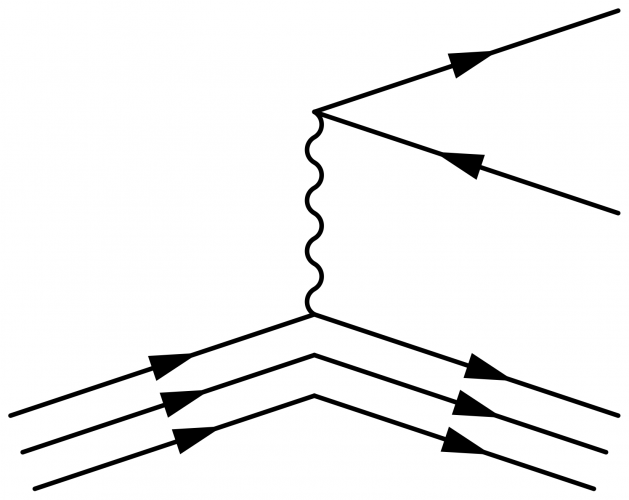
\begin{fmffile}{feyngraph} \begin{fmfgraph}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson}{v1,v3} % neutron \fmf{phantom}{i3,v3,o3} \fmffreeze \quark{qai}{0.0 ,1.0 }{0.96}{0, 0}{i3,v3} \quark{qbi}{0.04,1.0 }{1.00}{0, -8}{i3,v3} \quark{qci}{0.08,1.0 }{1.04}{0,-16}{i3,v3} \quark{qao}{0.0 ,1.0 }{1.04}{0, 0}{v3,o3} \quark{qbo}{0.0 ,0.96}{1.00}{0, -8}{v3,o3} \quark{qco}{0.0 ,0.92}{0.96}{0,-16}{v3,o3} \end{fmfgraph} \end{fmffile}
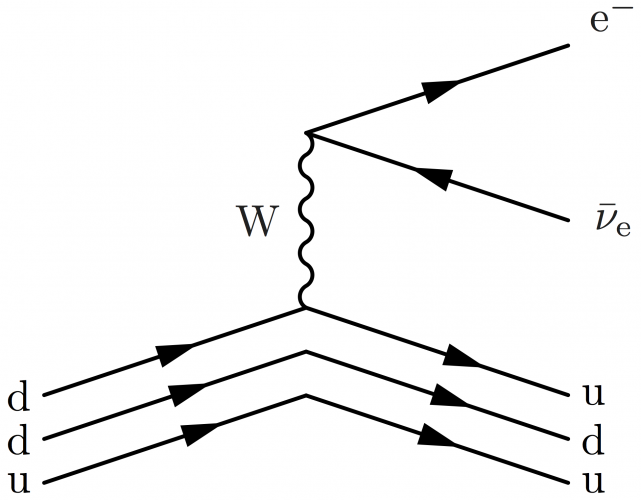
To include unique labels for each quark line, extend our \quark command:
\newcommand{\quark}[7]{ \fmfcmd{style_def quarkl#1 expr p = cdraw subpath (#4) of p shifted (#6); cfill (tarrow (p,(xpart(#4)+ypart(#4))*0.48*#5)) shifted (#6); if length("#3")=2: label.#3(btex {#2} etex, point ypart(#4) of p shifted (#6)) fi; % rt if length("#3")=3: label.#3(btex {#2} etex, point xpart(#4) of p shifted (#6)) fi; % lft enddef;} \fmf{quarkl#1,tension=0}{#7}}
with seven arguments (#1–#7):
- unique label of the arrow object (containing only letters);
- text label;
- label position:
lft(left) orrt(right) with no spaces; - two, comma-seperated values between
0and1, e.g.{0.1,0.9}, which allow you to shorten or lengthen either ends of the quark line; - value around
1to define the arrow head's position on the quark line; - two, comma-seperated values, e.g.
{1,-2}, to shift the line; - two or more, comma-seperated vertices.
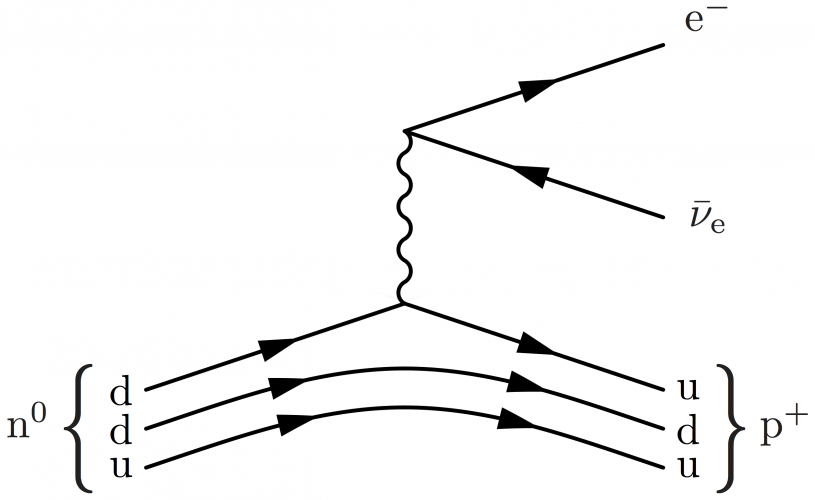
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmflabel{e$^-$}{o1} \fmflabel{$\bar\nu_\text{e}$}{o2} \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson,label=W,label.side=right}{v1,v3} % neutron \fmf{phantom}{i3,v3,o3} \fmffreeze \quark{qai}{d}{lft}{0,1}{0.90}{0, 0}{i3,v3} \quark{qbi}{d}{lft}{0,1}{1.00}{0,-10}{i3,v3} \quark{qci}{u}{lft}{0,1}{1.10}{0,-20}{i3,v3} \quark{qao}{u} {rt}{0,1}{1.10}{0, 0}{v3,o3} \quark{qbo}{d} {rt}{0,1}{1.00}{0,-10}{v3,o3} \quark{qco}{u} {rt}{0,1}{0.90}{0,-20}{v3,o3} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmflabel{e$^-$}{o1} \fmflabel{$\bar\nu_\text{e}$}{o2} \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson,label=W,l.s=right}{v1,v3} % neutron \fmf{phantom}{i3,v3,o3} \fmffreeze \quark{qai}{d}{lft}{0.0 ,1.0 }{0.94}{0, 0}{i3,v3} \quark{qbi}{d}{lft}{0.04,1.0 }{1.00}{0,-10}{i3,v3} \quark{qci}{u}{lft}{0.08,1.0 }{1.06}{0,-20}{i3,v3} \quark{qao}{u} {rt}{0.0 ,1.0 }{1.06}{0, 0}{v3,o3} \quark{qbo}{d} {rt}{0.0 ,0.96}{1.00}{0,-10}{v3,o3} \quark{qco}{u} {rt}{0.0 ,0.92}{0.94}{0,-20}{v3,o3} \end{fmfgraph*} \end{fmffile}
We can add curly braces of custom size (see this section):
\usepackage{scalerel} \newcommand{\mylbrace}[2]{\vspace{#2pt}\hspace{2pt}\scaleleftright[\dimexpr6pt+#1\dimexpr0.11pt]{\lbrace}{\rule[\dimexpr2pt-#1\dimexpr0.5pt]{-4pt}{#1pt}}{.}} \newcommand{\myrbrace}[2]{\vspace{#2pt}\scaleleftright[\dimexpr6pt+#1\dimexpr0.11pt]{.}{\rule[\dimexpr2pt-#1\dimexpr0.5pt]{-4pt}{#1pt}}{\rbrace}\hspace{2pt}}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,100) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmflabel{e$^-$}{o1} \fmflabel{$\bar\nu_\text{e}$}{o2} \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson,label=W,label.side=right}{v1,v3} % neutron \fmfv{l=$\text{n}^0$\mylbrace{32}{-9},l.d=16,l.a=-160}{i3} \fmfv{l=\myrbrace{32}{-9}$\text{p}^+$,l.d=16,l.a=-20}{o3} \fmf{phantom}{i3,v3,o3} \fmffreeze \quark{qai}{d}{lft}{0,1}{0.90}{0, 0}{i3,v3} \quark{qbi}{d}{lft}{0,1}{1.00}{0,-10}{i3,v3} \quark{qci}{u}{lft}{0,1}{1.10}{0,-20}{i3,v3} \quark{qao}{u} {rt}{0,1}{1.10}{0, 0}{v3,o3} \quark{qbo}{d} {rt}{0,1}{1.00}{0,-10}{v3,o3} \quark{qco}{u} {rt}{0,1}{0.90}{0,-20}{v3,o3} \end{fmfgraph*} \end{fmffile}
With curved lines:
\newcommand{\quark}[9]{ \fmfcmd{input TEX; style_def quark#1 expr p = pair a, b, m, n; if "#6"="left": a = point 0 of p; b = point length(p) of p + (#7); m = point length(p) of p + (#8); path q; q = a{m-a}..tension ypart(#4)..{right}b; label.lft(btex #2 etex, point xpart(#3) of q shifted (#5)) fi; if "#6"="right": a = point 0 of p + (#7); b = point length(p) of p; m = point 0 of p + (#8); path q; q = a{right}..tension ypart(#4)..{b-m}b; label.rt(btex #2 etex, point ypart(#3) of q shifted (#5)) fi; cdraw subpath (#3) of q shifted (#5); cfill (tarrow (q,(xpart(#3)+ypart(#3))*0.46*xpart(#4))) shifted (#5); enddef;} \fmf{quark#1,tension=0}{#9}}
with seven arguments (#1–#9):
- unique label of the arrow object (containing only letters);
- text label;
- two, comma-separated values between
0and1, e.g.{0.1,0.9}, which allow you to shorten or lengthen either ends of the quark line; - two, comma-separated: first value around
1to define the arrow head's position on the quark line, second value around1to set tension of curve (infinityfor straight lines); - two, comma-seperated values, e.g.
{1,-2}, to shift the line; - two, comma-seperated values, to shift the vertex;
- two, comma-seperated values, to shift the last point of a tangent;
- two or more, comma-seperated vertices.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmflabel{e$^-$}{o1} \fmflabel{$\bar\nu_\text{e}$}{o2} \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson}{v3,v1} % neutron \fmf{phantom}{i3,v3,o3} % to help \quark \fmffreeze \quark{qai}{d}{0.0 ,1.0 }{1.00,infinity}{0, 0}{left} {0, 0}{0,0}{i3,v3} \quark{qbi}{d}{0.04,1.0 }{1.00,1} {0, -9}{left} {0,-6}{0,0}{i3,v3} \quark{qci}{u}{0.08,1.0 }{1.02,1} {0,-18}{left} {0,-6}{0,0}{i3,v3} \quark{qao}{u}{0.0 ,1.0 }{1.00,infinity}{0, 0}{right}{0, 0}{0,0}{v3,o3} \quark{qbo}{d}{0.0 ,0.96}{0.89,1} {0, -9}{right}{0,-6}{0,0}{v3,o3} \quark{qco}{u}{0.0 ,0.92}{0.84,1} {0,-18}{right}{0,-6}{0,0}{v3,o3} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmflabel{e$^-$}{o1} \fmflabel{$\bar\nu_\text{e}$}{o2} \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson}{v3,v1} % neutron \fmf{phantom}{i3,v3,o3} % to help \quark \fmffreeze \fmfv{l=$\text{n}^0$\mylbrace{30}{-7},l.d=16,l.a=-160}{i3} \fmfv{l=\myrbrace{30}{-7}$\text{p}^+$,l.d=16,l.a=-20}{o3} \quark{qai}{d}{0,1}{1.00,infinity}{0, 0}{left} {0, 0}{0,0}{i3,v3} \quark{qbi}{d}{0,1}{1.05,1} {0, -9}{left} {0,-6}{0,0}{i3,v3} \quark{qci}{u}{0,1}{1.12,1} {0,-18}{left} {0,-6}{0,0}{i3,v3} \quark{qao}{u}{0,1}{1.00,infinity}{0, 0}{right}{0, 0}{0,0}{v3,o3} \quark{qbo}{d}{0,1}{0.85,1} {0, -9}{right}{0,-6}{0,0}{v3,o3} \quark{qco}{u}{0,1}{0.77,1} {0,-18}{right}{0,-6}{0,0}{v3,o3} \end{fmfgraph*} \end{fmffile}
Deep inelastic scattering
For deep inelastic scattering, also check out this DESY page with a gallery of Feynman diagrams.
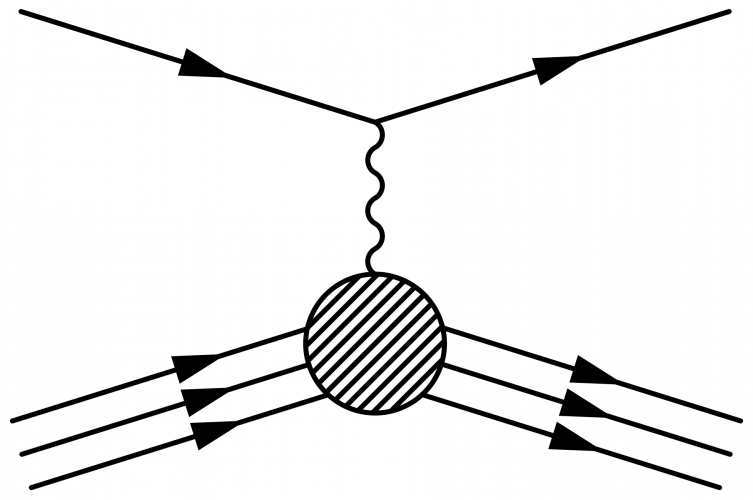
\fmfi allows to make lines that can be shifted and scaled, so you can make multiple line representing a proton. Also note that the \fmfblob hide the loose ends of these lines, as long as they are large enough and the lines are drawn before the blob.
Take for example elastic electron-proton scattering.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,80) \fmfleft{ip,il} \fmfright{op,ol} \fmfset{arrow_len}{10} % lepton \fmf{fermion}{il,vl,ol} % photon \fmf{photon,tension=1}{vl,vp} % proton \fmf{phantom}{ip,vp,op} \fmffreeze \fmf{phantom}{ip,vp} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-1.7, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted ( 1.7,-6)} \fmfblob{25}{vp} \fmf{phantom}{vp,op} \fmfi{fermion}{vpath (__vp,__op) scaled 1.05 shifted (-5.1, 6)} \fmfi{fermion}{vpath (__vp,__op) scaled 1.05 shifted (-7.0, 0)} \fmfi{fermion}{vpath (__vp,__op) scaled 1.05 shifted (-8.9,-6)} \fmffreeze \end{fmfgraph*} \end{fmffile}
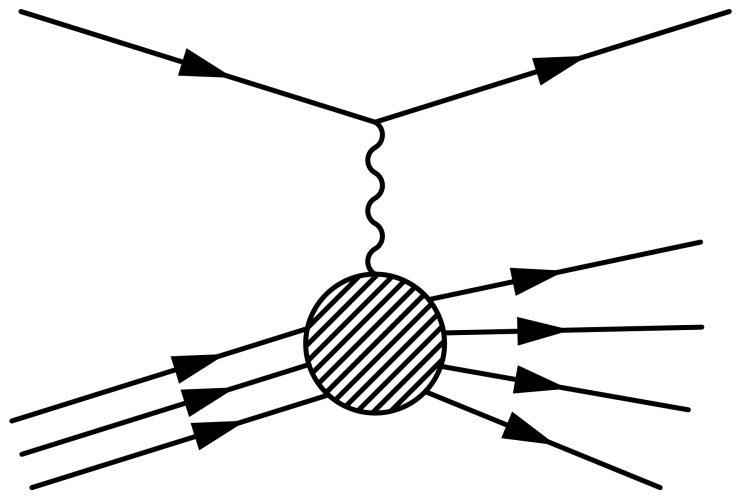
Electron-proton deep inelastic scattering:
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,80) \fmfleft{ip,il} \fmfright{x1,x2,x3,x4,o2,o3,o4,ol} \fmfset{arrow_len}{10} % lepton \fmf{fermion}{il,vl,ol} % photon \fmf{photon,tension=1}{vl,vp} % proton \fmf{phantom}{ip,vp,x1} \fmffreeze \fmf{phantom}{ip,vp} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-1.8, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted ( 1.8,-6)} % X \fmfshift{15 left}{x1,x2,x3,x4} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmf{phantom}{vp,x4} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.02 shifted ( 0.0,-6.0)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.00 shifted ( 0.0,-2.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 0.98 shifted ( 0.0, 2.0)} \fmfi{fermion}{vpath (__vp,__x4) scaled 0.96 shifted ( 0.0, 6.0)} \fmfblob{25}{vp} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,100) \fmfleft{i1,ip,i2,il,i3} \fmfright{x1,x2,x3,x4,o2,o3,o4,ol,o5} \fmfset{arrow_len}{10} % photon \fmf{photon,tension=0.25}{vl,vp} % lepton \fmf{fermion}{il,vl,ol} % proton \fmf{phantom}{ip,vp,x2} \fmffreeze \fmf{phantom}{ip,vp} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4,-6)} % X \fmfshift{15 left}{x1,x2,x3,x4} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmf{phantom}{vp,x4} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.08 shifted ( 0.0,-10.0)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.06 shifted ( 0.0,-5.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 1.04 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vp,__x4) scaled 1.02 shifted ( 0.0, 5.0)} \fmfblob{25}{vp} \end{fmfgraph*} \end{fmffile}
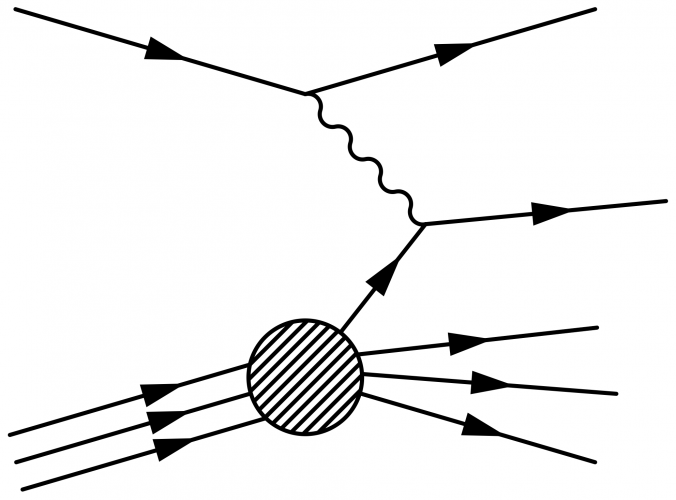
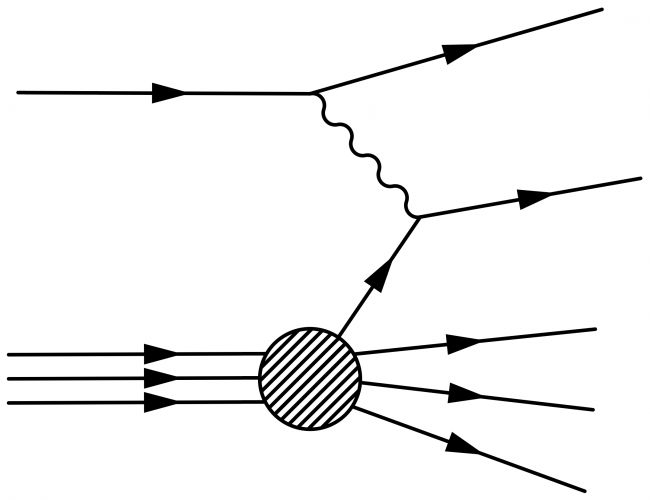
Deep inelastic scattering with a parton:
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,100) \fmfleft{ip,il} \fmfright{x1,x2,x3,o1,o2,o3,o4,ol} \fmfset{arrow_len}{10} % lepton \fmf{fermion}{il,vl} \fmf{fermion}{vl,ol} \fmf{phantom,tension=0.6}{vl,vp} % proton \fmf{phantom,tension=1}{ip,vp,x1} \fmffreeze \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-1.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted ( 1.4,-6)} \fmfblob{25}{vp} % X \fmf{fermion}{vp,x1} \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x2) scaled 0.98 shifted (0,2.2)} \fmfi{fermion}{vpath (__vp,__x3) scaled 0.92 shifted (0,4.5)} \fmffreeze % photon \fmf{photon}{vl,v} % parton \fmf{fermion}{vp,v,o2} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,140) \fmfleft{i1,ip,i2,il,i3} \fmfright{o1,x1,x2,x3,x4,o3,o3,o4,o5,ol,o5} \fmfset{arrow_len}{10} % photon \fmf{phantom,tension=0.30}{vl,vp} % lepton \fmf{fermion}{il,vl,ol} % proton \fmf{phantom}{ip,vp,x1} \fmffreeze \fmf{phantom}{ip,vp} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4,-6)} % X \fmfshift{15 left}{x1,x2,x3,x4} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmf{phantom}{vp,x4} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.08 shifted ( 0.0,-8.0)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.06 shifted ( 0.0,-2.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 1.04 shifted ( 0.0, 4.0)} \fmfblob{25}{vp} % parton \fmf{photon,tension=1}{vl,v} \fmf{fermion,tension=1}{vp,v,o3} \end{fmfgraph*} \end{fmffile}
Defining a new command in the preamble, we can add a curly brace of custom size (see this section):
\usepackage{scalerel} \newcommand{\mybrace}[1]{\scaleleftright[\dimexpr6pt+#1\dimexpr0.11pt]{.}{\rule[\dimexpr5pt-#1\dimexpr0.5pt]{-4pt}{#1pt}}{\rbrace}\hspace{-1pt}}
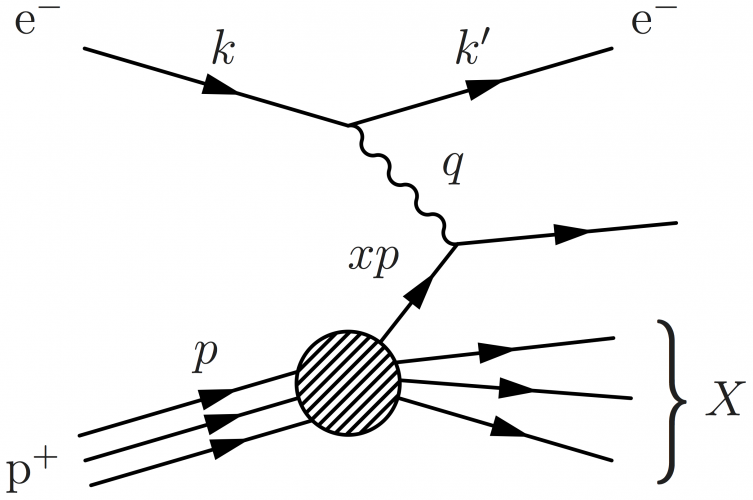
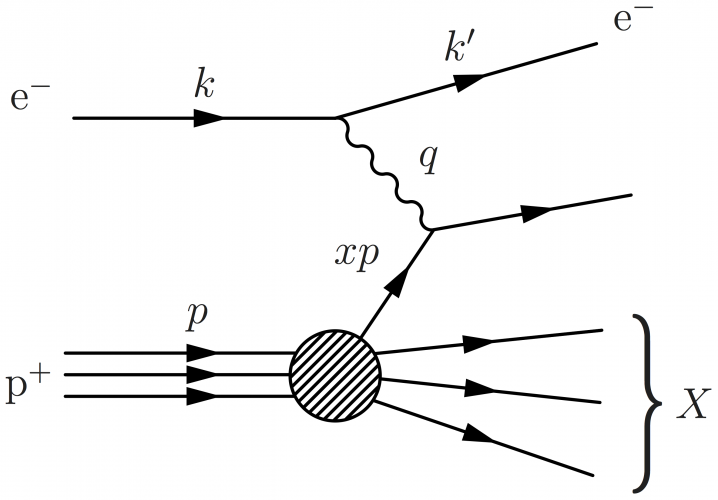
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,100) \fmfleft{ip,il} \fmfright{x1,x2,x3,o1,o2,o3,o4,ol} \fmfset{arrow_len}{10} % lepton \fmflabel{$\text{e}^-$}{il} \fmflabel{$\text{e}^-$}{ol} \fmf{fermion,label=$k$, label.side=left}{il,vl} \fmf{fermion,label=$k'$,label.side=left}{vl,ol} \fmf{phantom,tension=0.6}{vl,vp} % proton \fmfv{l=$\text{p}^+$,l.a=-160}{ip} % l.a = label.angle \fmf{phantom,tension=1}{ip,vp,x1} \fmffreeze \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01} \fmfi{fermion,label=$p$,label.side=left} {vpath (__ip,__vp) scaled 1.01 shifted (-1.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted ( 1.4,-6)} \fmfblob{25}{vp} % X \fmfv{l=\mybrace{40} $X$,l.a=10}{x2} \fmf{fermion}{vp,x1} \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x2) scaled 0.98 shifted (0,2.2)} \fmfi{fermion}{vpath (__vp,__x3) scaled 0.92 shifted (0,4.5)} \fmffreeze % photon \fmf{photon,label=\vspace{-4pt}\hspace{5pt}{$q$},label.side=left}{vl,v} % parton \fmf{fermion,label=$xp$,label.side=left}{vp,v} \fmf{fermion}{v,o2} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,140) \fmfleft{i1,ip,i2,il,i3} \fmfright{o1,x1,x2,x3,x4,o3,o3,o4,o5,ol,o5} \fmfset{arrow_len}{10} \fmf{phantom,tension=0.29}{vl,vp} % lepton \fmflabel{$\text{e}^-$}{il} \fmflabel{$\text{e}^-$}{ol} \fmf{fermion,label=$k$, label.side=left}{il,vl} \fmf{fermion,label=$k'$,label.side=left}{vl,ol} % proton \fmfv{l=$\text{p}^+$,l.a=-160}{ip} \fmf{phantom}{ip,vp,x1} \fmffreeze \fmf{phantom}{ip,vp} \fmfi{fermion,label=$p$,label.side=left} {vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4,-6)} % X \fmfv{l=\mybrace{50}$X$,l.d=20,l.a=-2}{x2} \fmfshift{12 left}{x1,x2,x3,x4} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmf{phantom}{vp,x4} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.08 shifted ( 0.0,-8.0)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.06 shifted ( 0.0,-2.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 1.04 shifted ( 0.0, 4.0)} \fmfblob{25}{vp} % photon & parton \fmf{photon,tension=1,label=\vspace{-4pt}\hspace{5pt}{$q$},label.side=left}{vl,v} \fmf{fermion,label=$xp$,label.side=left}{vp,v} \fmf{fermion}{v,o3} \end{fmfgraph*} \end{fmffile}
Tau decay
Examples of leptonic and hadronic tau lepton decay
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,90) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % boson \fmf{boson,label=$\text{W}^\pm$,label.side=left}{v3,v1} % leptons \fmflabel{$\tau^\pm$}{i3} \fmflabel{$\nu_\tau$}{o3} \fmf{fermion}{i3,v3,o3} % decay \fmflabel{$\ell^\pm$}{o1} \fmflabel{$\nu_\ell$}{o2} \fmf{fermion,tension=0}{o2,v1,o1} \fmf{phantom}{i1,v1,o1} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,90) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % boson \fmf{boson,label=$\text{W}^\pm$,label.side=left}{v3,v1} % leptons \fmflabel{$\tau^\pm$}{i3} \fmflabel{$\nu_\tau$}{o3} \fmf{fermion}{i3,v3,o3} % decay \fmflabel{$q$}{o1} \fmflabel{$\overline{q}'$}{o2} \fmf{fermion,tension=0}{o2,v1,o1} \fmf{phantom}{i1,v1,o1} \fmffreeze \fmfv{l.d=82,l.a=12,l={\mybrace{68}{-28}$\pi^\pm$,, $\text{a}_1^\pm$,, $\rho^\pm$,, $\ldots$}}{v1} \end{fmfgraph*} \end{fmffile}
Where \mybrace is defined in the preamble as (see this section):
\usepackage{scalerel} \newcommand{\mybrace}[2]{\vspace{#2pt}\scaleleftright[\dimexpr5pt+#1\dimexpr0.06pt]{.}{\rule[\dimexpr2pt-#1\dimexpr0.5pt]{-4pt}{#1pt}}{\rbrace}\hspace{4pt}}
B meson decay
Examples of B meson decay, using the following code in the preamble.
\newcommand{\quark}[9]{ \fmfcmd{ %input TEX; input latexmp; setupLaTeXMP(packages="amssymb,amsmath"); style_def quark#1 expr p = pair a, b, m, n; if (substring (0,4) of "#6" = "left") or (substring (1,5) of "#6" = "left"): a = point 0 of p; b = point length(p) of p + (#7); m = point length(p) of p + (#8); path q; q = a{m-a}..tension ypart(#4)..{right}b; label.lft(btex #2 etex, point xpart(#3) of q shifted (#5)) fi; if (substring (0,5) of "#6" = "right") or (substring (1,6) of "#6" = "right"): a = point 0 of p + (#7); b = point length(p) of p; m = point 0 of p + (#8); path q; q = a{right}..tension ypart(#4)..{b-m}b; label.rt(btex #2 etex, point ypart(#3) of q shifted (#5)) fi; cdraw subpath (#3) of q shifted (#5); if substring (0,1) of "#6" = "-": cfill (tarrow (reverse(q),(xpart(#3)+ypart(#3))*0.46*xpart(#4))) shifted (#5); else: cfill (tarrow (q,(xpart(#3)+ypart(#3))*0.46*xpart(#4))) shifted (#5); fi; enddef;} \fmf{quark#1,tension=0}{#9}} \usepackage{scalerel} \newcommand{\mylbrace}[2]{\vspace{#2pt}\hspace{4pt}\scaleleftright[\dimexpr6pt+#1\dimexpr0.11pt]{\lbrace}{\rule[\dimexpr2pt-#1\dimexpr0.5pt]{-4pt}{#1pt}}{.}} \newcommand{\myrbrace}[2]{\vspace{#2pt}\scaleleftright[\dimexpr6pt+#1\dimexpr0.11pt]{.}{\rule[\dimexpr2pt-#1\dimexpr0.5pt]{-4pt}{#1pt}}{\rbrace}\hspace{4pt}}
Taking (b,q,c) = (bbar,u,cbar), (b,ubar,c), (bbar,d,cbar), etc.:
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmflabel{$\ell^\pm$}{o1} \fmflabel{$\nu_\ell$}{o2} \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson,label=$\text{W}^\pm$,label.side=left}{v3,v1} % neutron \fmf{phantom}{i3,v3,o3} % to help \quark \fmffreeze \fmfv{l=\parbox{10mm}{\centering B meson}\mylbrace{26}{-3},l.d=16,l.a=-160}{i3} \fmfv{l=\myrbrace{26}{-3}\parbox{10mm}{\centering D meson},l.d=16,l.a=-20}{o3} %\fmfiv{l=$\overline{\text{b}}$,l.d=3,l.a=180}{vloc(__i3)} %\fmfiv{l=$\overline{\text{c}}$,l.d=3,l.a= 0}{vloc(__o3)} \quark{qai}{$b$}{0,1}{1.00,infinity}{0, 0}{left}{0, 0}{0,0}{i3,v3} \quark{qbi}{$q$}{0,1}{1.09,1} {0,-14}{left}{0,-6}{0,0}{i3,v3} \quark{qao}{$c$}{0,1}{1.00,infinity}{0, 0}{right}{0, 0}{0,0}{v3,o3} \quark{qbo}{$q$}{0,1}{0.84,1} {0,-14}{right}{0,-6}{0,0}{v3,o3} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,80) \fmfset{arrow_len}{10} \fmfstraight \fmfleft{i3,i1} \fmfright{o3,o2,o1} % fermions \fmflabel{$\ell^\pm$}{o1} \fmflabel{$\nu_\ell$}{o2} \fmf{phantom}{i1,v1,o1} \fmf{fermion,tension=0}{o2,v1,o1} % boson \fmf{boson,label=$\text{W}^\pm$,label.side=left}{v3,v1} % neutron \fmf{phantom}{i3,v3,o3} % to help \quark \fmffreeze \fmfv{l=\parbox{10mm}{\centering B meson}\mylbrace{26}{-2},l.d=16,l.a=-160}{i3} \fmfv{l=\myrbrace{26}{-2}\parbox{10mm}{\centering D meson},l.d=16,l.a=-20}{o3} \fmfiv{l=$\overline{\text{b}}$,l.d=3,l.a=180}{vloc(__i3)} \fmfiv{l=$\overline{\text{c}}$,l.d=3,l.a= 0}{vloc(__o3)} \quark{qai}{}{0,1}{1.00,infinity}{0, 0}{-left}{0, 0}{0,0}{i3,v3} \quark{qbi}{$q$}{0,1}{1.05,1} {0,-14}{left}{0,-6}{0,0}{i3,v3} \quark{qao}{}{0,1}{0.95,infinity}{0, 0}{-right}{0, 0}{0,0}{v3,o3} \quark{qbo}{$q$}{0,1}{0.85,1} {0,-14}{right}{0,-6}{0,0}{v3,o3} \end{fmfgraph*} \end{fmffile}
Proton-proton collisions with a hard process
Here are some proton-proton collisions with hard processes. Note the use of \fmfshift to shorten the proton debris lines, and make the hard process stick out, without changing the aspect ratio of diagram's other parts.
Full code for a multipage PDF including all figures below can be found here.
A generic proces:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,160) \fmfleft{i1,iq,i2,ip,i3} \fmfright{y1,y2,y3,o1,o2,o3,o4,o5,x3,x2,x1} \fmfset{arrow_len}{10} % skeleton \fmf{phantom,tension=0.50}{vq,vp} \fmf{phantom}{ip,vp,x1} \fmf{phantom}{iq,vq,y1} \fmffreeze % parton \fmf{fermion,tension=2,label=$x_1p_1$,label.side=right}{vp,v} \fmf{fermion,tension=2,label=$x_2p_2$,label.side=left}{vq,v} % hard interaction \fmf{phantom,tension=1}{v,o2} % to help \fmfi \fmf{phantom,tension=1}{v,o3} % to help \fmfi \fmf{phantom,tension=1}{v,o4} % to help \fmfi \fmffreeze \fmfi{fermion}{vpath (__v,__o2) scaled 1.01 shifted ( 0,-2)} \fmfi{fermion}{vpath (__v,__o3) scaled 1.01 shifted ( 0, 0)} \fmfi{fermion}{vpath (__v,__o4) scaled 1.01 shifted ( 0, 2)} \fmfblob{20}{v} % proton 1 \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{ip} \fmf{phantom}{ip,vp} \fmfi{fermion,l=$p_1$,l.s=left,l.d=8} {vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4,-6)} % proton 2 \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{iq} \fmf{phantom}{iq,vq} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion,l=$p_2$,l.s=right,l.d=8} {vpath (__iq,__vq) scaled 1.01 shifted (-2.4,-6)} % X 2 \fmfshift{25 left}{x1} \fmfshift{20 left}{x2,x3} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.0 shifted ( 0.0, 2.0)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.0 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 1.0 shifted ( 0.0,-2.0)} \fmfblob{25}{vp} % X 2 \fmfshift{25 left}{y1} \fmfshift{20 left}{y2,y3} \fmf{phantom}{vq,y1} % to help \fmfi \fmf{phantom}{vq,y2} % to help \fmfi \fmf{phantom}{vq,y3} % to help \fmfi \fmfi{fermion}{vpath (__vq,__y1) scaled 1.0 shifted ( 0.0,-2.0)} \fmfi{fermion}{vpath (__vq,__y2) scaled 1.0 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vq,__y3) scaled 1.0 shifted ( 0.0, 2.0)} \fmfblob{25}{vq} \end{fmfgraph*} \end{fmffile}
Drell-Yan:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,160) \fmfleft{i1,iq,i2,ip,i3} \fmfright{y1,y2,y3,o1,f1,o2,o3,o4,f2,o5,x3,x2,x1} \fmfset{arrow_len}{10} % skeleton \fmf{phantom,tension=0.48}{vq,vp} \fmf{phantom}{ip,vp,x1} \fmf{phantom}{iq,vq,y1} \fmffreeze % parton \fmfv{l=$x_1p_1$,l.a=-90,l.d=22}{vp} % cheat: actually a line label \fmfv{l=$x_2p_2$,l.a=90,l.d=22}{vq} % cheat: actually a line label \fmf{fermion,tension=1.6}{vp,v} \fmf{fermion,tension=1.6}{v,vq} % hard process \fmfshift{20 right}{f1,f2} \fmfv{l.a=-25,l.d=3,l=$\ell^+$}{f1} \fmfv{l.a=25,l.d=5,l=$\ell^-$}{f2} \fmf{boson,tension=2,label=$\text{Z}^0/\gamma^*$,label.side=left}{v,vf} \fmf{fermion,tension=2}{f1,vf,f2} % proton 1 \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{ip} \fmf{phantom}{ip,vp} \fmfi{fermion,l=$p_1$,l.s=left,l.d=8} {vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4,-6)} % proton 2 \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{iq} \fmf{phantom}{iq,vq} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion,l=$p_2$,l.s=right,l.d=8} {vpath (__iq,__vq) scaled 1.01 shifted (-2.4,-6)} % X 2 \fmfshift{25 left}{x1} \fmfshift{20 left}{x2,x3} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.0 shifted ( 0.0, 2.0)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.0 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 1.0 shifted ( 0.0,-2.0)} \fmfblob{25}{vp} % X 2 \fmfshift{25 left}{y1} \fmfshift{20 left}{y2,y3} \fmf{phantom}{vq,y1} % to help \fmfi \fmf{phantom}{vq,y2} % to help \fmfi \fmf{phantom}{vq,y3} % to help \fmfi \fmfi{fermion}{vpath (__vq,__y1) scaled 1.0 shifted ( 0.0,-2.0)} \fmfi{fermion}{vpath (__vq,__y2) scaled 1.0 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vq,__y3) scaled 1.0 shifted ( 0.0, 2.0)} \fmfblob{25}{vq} \end{fmfgraph*} \end{fmffile}
Higgs production via gluon-gluon fusion:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,160) \fmfleft{i1,iq,i2,ip,i3} \fmfright{y1,y2,y3,o1,o2,o3,o4,o5,x3,x2,x1} \fmfset{arrow_len}{10} \fmfset{curly_len}{8} % skeleton \fmf{phantom,tension=0.48}{vq,vp} \fmf{phantom}{ip,vp,x1} \fmf{phantom}{iq,vq,y1} \fmffreeze % parton \fmf{gluon,tension=1.4,label=$x_1p_1$,label.side=left}{v1,vp} \fmf{gluon,tension=1.4,label=$x_2p_2$,label.side=left}{vq,v2} % hard process \fmfshift{20 right}{o3} \fmfv{l=H}{o3} \fmf{fermion,tension=0.3,arrow.size=2mm}{v1,v2} \fmf{fermion,tension=2.0}{v1,vh,v2} \fmf{dashes,tension=2.5}{vh,o3} % proton 1 \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{ip} \fmf{phantom}{ip,vp} \fmfi{fermion,l=$p_1$,l.s=left,l.d=8} {vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion}{vpath (__ip,__vp) scaled 1.01 shifted (-2.4,-6)} % proton 2 \fmfv{l=$\text{p}^+$,l.a=180,l.d=10}{iq} \fmf{phantom}{iq,vq} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 6)} \fmfi{fermion}{vpath (__iq,__vq) scaled 1.01 shifted (-2.4, 0)} \fmfi{fermion,l=$p_2$,l.s=right,l.d=8} {vpath (__iq,__vq) scaled 1.01 shifted (-2.4,-6)} % X 2 \fmfshift{25 left}{x1} \fmfshift{20 left}{x2,x3} \fmf{phantom}{vp,x1} % to help \fmfi \fmf{phantom}{vp,x2} % to help \fmfi \fmf{phantom}{vp,x3} % to help \fmfi \fmfi{fermion}{vpath (__vp,__x1) scaled 1.0 shifted ( 0.0, 2.0)} \fmfi{fermion}{vpath (__vp,__x2) scaled 1.0 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vp,__x3) scaled 1.0 shifted ( 0.0,-2.0)} \fmfblob{25}{vp} % X 2 \fmfshift{25 left}{y1} \fmfshift{20 left}{y2,y3} \fmf{phantom}{vq,y1} % to help \fmfi \fmf{phantom}{vq,y2} % to help \fmfi \fmf{phantom}{vq,y3} % to help \fmfi \fmfi{fermion}{vpath (__vq,__y1) scaled 1.0 shifted ( 0.0,-2.0)} \fmfi{fermion}{vpath (__vq,__y2) scaled 1.0 shifted ( 0.0, 0.0)} \fmfi{fermion}{vpath (__vq,__y3) scaled 1.0 shifted ( 0.0, 2.0)} \fmfblob{25}{vq} \end{fmfgraph*} \end{fmffile}
Diffractive proton-proton collisions
Diffractive processes involving a Pomeron, after this ALICE, this CMS (FSQ-15-005) and this ATLAS (ATL-PHYS-PROC-2016-079) paper. Note the Pomeron symbol is made with ${\rm I\!P}$ instead of ${\mathbb{P}$.
Full code for a multipage PDF including all figures below can be found here.
Elastic scattering with Pomeron exchange:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,80) \fmfleft{iq,ip} \fmfright{oq,op} % proton 1 \fmflabel{$\text{p}^+$}{ip} \fmflabel{$\text{p}^+$}{op} \fmf{fermion,width=1.5}{ip,vp,op} % proton 2 \fmflabel{$\text{p}^+$}{iq} \fmflabel{$\text{p}^+$}{oq} \fmf{fermion,width=1.5}{iq,vq,oq} % pomeron \fmfv{decor.shape=circle,decor.filled=full,decor.size=6}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6}{vq} \fmf{double,tension=0.9,label=${\rm I\!P}$,label.side=right}{vp,vq} \end{fmfgraph*} \end{fmffile}
Single diffraction (SD):
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,80) \fmfleft{iq,ip} \fmfright{oq,op} % proton 1 \fmflabel{$\text{p}^+$}{ip} \fmflabel{$\text{p}^+$}{op} \fmf{fermion,width=1.5}{ip,vp,op} % proton 2 \fmflabel{$\text{p}^+$}{iq} \fmf{fermion,width=1.5}{iq,vq} \fmf{phantom}{vq,oq} % pomeron \fmf{double,tension=0.9,label=${\rm I\!P}$,label.side=right}{vp,vq} \fmffreeze % single diffraction \fmfshift{5 up}{oq} \fmfv{l=Y,l.a=-10,l.d=12}{oq} \fmfi{fermion}{vpath (__vq,__oq) scaled 1.01 shifted(4, 2) rotatedaround(vloc(__vq), 10)} \fmfi{fermion}{vpath (__vq,__oq) scaled 1.01 shifted(4, 0) rotatedaround(vloc(__vq), 0)} \fmfi{fermion}{vpath (__vq,__oq) scaled 1.01 shifted(4,-2) rotatedaround(vloc(__vq),-10)} % vertices \fmfv{decor.shape=circle,decor.filled=full,decor.size=6}{vp} \fmfblob{20}{vq} \end{fmfgraph*} \end{fmffile}
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,80) \fmfleft{iq,ip} \fmfright{oq,op} % proton 1 \fmflabel{$\text{p}^+$}{ip} \fmf{fermion,width=1.5}{ip,vp} \fmf{phantom}{vp,op} % proton 2 \fmflabel{$\text{p}^+$}{iq} \fmflabel{$\text{p}^+$}{oq} \fmf{fermion,width=1.5}{iq,vq,oq} % pomeron \fmf{double,tension=0.9,label=${\rm I\!P}$,label.side=right}{vp,vq} \fmffreeze % single diffraction \fmfshift{5 down}{op} \fmfv{l=X,l.a=10,l.d=12}{op} \fmfi{fermion}{vpath (__vp,__op) scaled 1.01 shifted(4, 2) rotatedaround(vloc(__vp), 10)} \fmfi{fermion}{vpath (__vp,__op) scaled 1.01 shifted(4, 0) rotatedaround(vloc(__vp), 0)} \fmfi{fermion}{vpath (__vp,__op) scaled 1.01 shifted(4,-2) rotatedaround(vloc(__vp),-10)} % vertices \fmfv{decor.shape=circle,decor.filled=full,decor.size=6}{vp} \fmfblob{20}{vp} \end{fmfgraph*} \end{fmffile}
Double diffraction (DD):
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,80) \fmfleft{iq,ip} \fmfright{oq,op} % proton 1 \fmflabel{$\text{p}^+$}{ip} \fmf{fermion,width=1.5}{ip,vp} \fmf{phantom}{vp,op} % proton 2 \fmflabel{$\text{p}^+$}{iq} \fmf{fermion,width=1.5}{iq,vq} \fmf{phantom}{vq,oq} % pomeron \fmf{double,tension=0.9,label=${\rm I\!P}$,label.side=right}{vp,vq} \fmffreeze % double diffraction \fmfshift{5 down}{op} \fmfshift{5 up}{oq} \fmfv{l=X,l.a=10,l.d=12}{op} \fmfv{l=Y,l.a=-10,l.d=12}{oq} \fmfi{fermion}{vpath (__vp,__op) scaled 1.01 shifted(4, 2) rotatedaround(vloc(__vp), 10)} \fmfi{fermion}{vpath (__vp,__op) scaled 1.01 shifted(4, 0) rotatedaround(vloc(__vp), 0)} \fmfi{fermion}{vpath (__vp,__op) scaled 1.01 shifted(4,-2) rotatedaround(vloc(__vp),-10)} \fmfi{fermion}{vpath (__vq,__oq) scaled 1.01 shifted(4, 2) rotatedaround(vloc(__vq), 10)} \fmfi{fermion}{vpath (__vq,__oq) scaled 1.01 shifted(4, 0) rotatedaround(vloc(__vq), 0)} \fmfi{fermion}{vpath (__vq,__oq) scaled 1.01 shifted(4,-2) rotatedaround(vloc(__vq),-10)} % vertices \fmfblob{20}{vp} \fmfblob{20}{vq} \end{fmfgraph*} \end{fmffile}
Central diffraction:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,80) \fmfleft{iq,ip} \fmfright{oq,oc,op} % proton 1 \fmflabel{$\text{p}^+$}{ip} \fmflabel{$\text{p}^+$}{op} \fmf{fermion,width=1.5}{ip,vp,op} % proton 2 \fmflabel{$\text{p}^+$}{iq} \fmflabel{$\text{p}^+$}{oq} \fmf{fermion,width=1.5}{iq,vq,oq} % pomeron \fmfv{decor.shape=circle,decor.filled=full,decor.size=6}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6}{vq} \fmf{double,tension=0.9,label=${\rm I\!P}$,label.side=right}{vp,v,vq} \fmffreeze % single diffraction \fmfv{l=Z,l.a=0,l.d=12}{oc} \fmf{phantom}{v,oc} \fmfshift{12 left}{oc} \fmfi{fermion}{vpath (__v,__oc) scaled 1.01 shifted(4, 2) rotatedaround(vloc(__v), 10)} \fmfi{fermion}{vpath (__v,__oc) scaled 1.01 shifted(4, 0) rotatedaround(vloc(__v), 0)} \fmfi{fermion}{vpath (__v,__oc) scaled 1.01 shifted(4,-2) rotatedaround(vloc(__v),-10)} \fmfblob{20}{v} \end{fmfgraph*} \end{fmffile}
Inelastic and non-diffractive:
\large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,80) \fmfleft{iq,ip} \fmfright{o} % proton 1 \fmflabel{$\text{p}^+$}{ip} \fmf{fermion,width=1.5}{ip,v} % proton 2 \fmflabel{$\text{p}^+$}{iq} \fmf{fermion,width=1.5}{iq,v} \fmf{phantom,tension=2}{v,o} \fmffreeze % X \fmfv{l=X,l.a=0,l.d=16}{o} \fmfi{fermion}{vpath (__v,__o) scaled 1.01 shifted(6, 4) rotatedaround(vloc(__v), 24)} \fmfi{fermion}{vpath (__v,__o) scaled 1.01 shifted(6, 2) rotatedaround(vloc(__v), 12)} \fmfi{fermion}{vpath (__v,__o) scaled 1.01 shifted(6, 0) rotatedaround(vloc(__v), 0)} \fmfi{fermion}{vpath (__v,__o) scaled 1.01 shifted(6,-2) rotatedaround(vloc(__v),-12)} \fmfi{fermion}{vpath (__v,__o) scaled 1.01 shifted(6,-4) rotatedaround(vloc(__v),-24)} \fmfblob{30}{v} \end{fmfgraph*} \end{fmffile}
Anomalous momentum measurement (g-2)
The text colors in the diagrams below are defined with the following in the preamble:
\usepackage{xcolor} \definecolor{myblue}{rgb}{.1,.1,.7} \definecolor{mygreen}{rgb}{.1,.6,.1}
Tree level of photon-tautau vertex:
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,100) \fmfbottom{f2,f1} \fmftop{g} \fmf{boson,t=1}{g,v} \fmf{fermion,f=(.1,,.6,,.1)}{f2,v1} \fmf{plain,f=(.1,,.6,,.1),t=0.9}{v1,v,v2} \fmf{fermion,f=(.1,,.6,,.1)}{v2,f1} \fmfv{l.a=-50,l.d=8,l=$\gamma$}{g} \fmfv{l.a=-25,l=\color{mygreen}$\tau$}{f1} \fmfv{l.a=-155,l=\color{mygreen}$\tau$}{f2} \fmffreeze \fmf{boson,right=0.36,label=$\gamma$,l.s=right}{v1,v2} \end{fmfgraph*} \end{fmffile}
Photon loop:
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,100) \fmfbottom{f2,f1} \fmftop{g} \fmf{boson,t=1}{g,v} \fmf{fermion,f=(.1,,.6,,.1)}{f2,v1} \fmf{plain,f=(.1,,.6,,.1),t=0.9}{v1,v,v2} \fmf{fermion,f=(.1,,.6,,.1)}{v2,f1} \fmfv{l.a=-50,l.d=8,l=$\gamma$}{g} \fmfv{l.a=-25,l=\color{mygreen}$\tau$}{f1} \fmfv{l.a=-155,l=\color{mygreen}$\tau$}{f2} \fmffreeze \fmf{boson,right=0.36,label=$\gamma$,l.s=right}{v1,v2} \end{fmfgraph*} \end{fmffile}
With vacuum polarization quark loop:
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(160,120) \fmfbottom{f2,f1} \fmftop{g} \fmf{boson,t=1}{g,v} \fmf{fermion,f=(.1,,.6,,.1)}{f2,v1} \fmf{fermion,f=(.1,,.6,,.1),t=0.6}{v1,v,v2} \fmf{fermion,f=(.1,,.6,,.1)}{v2,f1} \fmfv{l.a=-50,l.d=8,l=$\gamma$}{g} \fmfv{l.a=-25,l=\color{mygreen}$\tau$}{f1} \fmfv{l.a=-155,l=\color{mygreen}$\tau$}{f2} \fmffreeze \fmf{boson,t=2}{v1,vl1} \fmf{boson,t=2}{vl2,v2} \fmf{fermion,left=1,tension=1,label=\Large$q$}{vl1,vl2,vl1} \end{fmfgraph*} \end{fmffile}
Vertex with blob:
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,100) \fmfbottom{f2,f1} \fmftop{g} \fmf{boson,t=1.3}{g,v} \fmf{fermion,f=(.1,,.6,,.1)}{f2,v,f1} \fmfv{l.a=-25,l=\color{mygreen}$\tau$}{f1} \fmfv{l.a=-155,l=\color{mygreen}$\tau$}{f2} \fmfv{decor.shape=circle,decor.filled=shaded, decor.size=28,f=(.1,,.1,,.7)}{v} \fmfv{l.a=-50,l.d=8,l=$\gamma$}{g} \end{fmfgraph*} \end{fmffile}
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,100) \fmfbottom{f2,f1} \fmftop{g} \fmf{boson,t=1.3}{g,v} \fmf{fermion,f=(.1,,.6,,.1)}{f2,v,f1} \fmfv{l.a=-50,l.d=8,l=$\gamma$}{g} \fmfv{l.a=-25,l=\color{mygreen}$\tau$}{f1} \fmfv{l.a=-155,l=\color{mygreen}$\tau$}{f2} \fmfv{decor.shape=circle,decor.filled=empty,decor.size=35, f=(.1,,.1,,.7),b=(.92,,.92,,.98),l=\large\color{myblue}$g-2$,l.a=0,l.d=0}{v} \end{fmfgraph*} \end{fmffile}
\LARGE \begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,100) \fmfbottom{f2,f1} \fmftop{g} \fmf{boson,t=1}{g,v} \fmf{fermion,f=(.1,,.6,,.1)}{f2,v1} \fmf{dashes,left=0.48,t=0.7}{v1,v} \fmf{dashes,left=0.48,t=0.7,l.d=1pt,label=\Large slepton}{v,v2} \fmf{fermion,f=(.1,,.6,,.1)}{v2,f1} \fmf{phantom,t=0.3}{v2,v1} \fmfv{l.a=-25,l=\color{mygreen}$\tau$}{f1} \fmfv{l.a=-155,l=\color{mygreen}$\tau$}{f2} \fmffreeze \fmf{fermion,l.s=right,l.d=4,l.s=right, label=\huge$\substack{\text{dark}\\\text{matter}}$}{v1,v2} \fmfv{l.a=-50,l.d=8,l=$\gamma$}{g} \end{fmfgraph*} \end{fmffile}
Lepton flavor violating decays
Some examples of lepton flavor violating (LFV) decays of heavy leptons (muon, tau), which is possible in the Standard Model thanks to neutrino oscillations, but still heavily suppressed due to the small neutrino masses.
LVF decay of a heavy leptons (muon, tau) to a lepton plus photon.
\begin{fmffile}{feyngraph} \large \begin{fmfgraph*}(170,50) \fmfleft{i1,i2} \fmfright{o1,o2} \fmftop{t1,t2} % fermion lines \fmf{fermion}{i1,v1} % lepton line in \fmf{plain,l.d=3,label=$\nu_\ell$\;,t=1.5}{v1,x} % left neutrino line \fmf{plain,l.d=3,label=\;$\nu_{\ell'}$,t=1.5}{x,v2} % right neutrino line \fmf{fermion}{v2,o1} % lepton line out \fmfv{decor.shape=cross,decor.size=10}{x} % cross \fmffreeze % loop \fmf{phantom,t=1}{vl,i2} % support left \fmf{phantom,t=1.8}{vl,vr} % support middle \fmf{phantom,t=1}{vr,o2} % support right \fmf{boson,left=0.25,t=1.2}{v1,vl,vr,v2} % loop % photon \fmfshift{30 left}{t2} \fmf{boson,t=0}{vr,t2} % photon % labels \fmfv{l.d=5,l.a=180,l=$\ell^-$}{i1} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o1} \fmfv{l.d=8,l.a=70,l=$\mathrm{W}^-$}{vl} \fmfv{l.d=5,l.a=15,l=$\gamma$}{t2} \end{fmfgraph*} \end{fmffile}
LVF decay of a heavy leptons (muon, tau) to a three leptons, which proceeds through a penguin diagram.
\begin{fmffile}{feyngraph} \large \begin{fmfgraph*}(140,60) \fmfstraight \fmfleft{i1,i2,i3} \fmfright{o1,o2,o3} \fmftop{t1,t2} % fermion lines \fmf{fermion}{i1,v1} % lepton line in \fmf{plain,l.d=3,label=$\nu_\ell$\;,t=1.5}{v1,x} % left neutrino line \fmf{plain,l.d=3,label=\;$\nu_{\ell'}$,t=1.5}{x,v2} % right neutrino line \fmf{fermion}{v2,o1} % lepton line out \fmfv{decor.shape=cross,decor.size=10}{x} % cross \fmffreeze % loop \fmf{phantom,t=1.7}{vl,i2} % support left \fmf{phantom,t=2.4}{vl,vr} % support middle \fmf{phantom,t=1.7}{vr,o2} % support right \fmf{boson,left=0.25,t=0.7}{v1,vl,vr,v2} % loop \fmffreeze % photon \fmf{phantom,t=0.9}{t1,vg} % support \fmfshift{5 right}{o2} \fmfshift{5 right}{o3} \fmf{boson,t=1,l.d=4,label=$\gamma$}{vr,vg} % photon \fmf{fermion,t=1.8}{o3,vg,o2} % fermion % labels \fmfv{l.d=5,l.a=180,l=$\ell^-$}{i1} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o1} \fmfv{l.d=5,l.a=-10,l=$\ell'^-$}{o2} \fmfv{l.d=5,l.a=20,l=$\ell'^+$}{o3} \fmfv{l.d=8,l.a=70,l=$\mathrm{W}^-$}{vl} \end{fmfgraph*} \end{fmffile}
LVF decay of a heavy leptons (muon, tau) to a lepton and a photon through a LQ mediator.
\begin{fmffile}{feyngraph} \large \begin{fmfgraph*}(170,50) \fmfleft{i1,i2} \fmfright{o1,o2} \fmftop{t1,t2} % fermion lines \fmf{fermion}{i1,v1} % lepton line in \fmf{fermion,l.d=6,label=$q$,t=0.75}{v1,v2} % quark line \fmf{fermion}{v2,o1} % lepton line out \fmffreeze % loop \fmf{phantom,t=1}{vl,i2} % support left \fmf{phantom,t=1.8}{vl,vr} % support middle \fmf{phantom,t=1}{vr,o2} % support right \fmf{boson,left=0.25,t=1.2}{v1,vl,vr,v2} % loop % photon \fmfshift{30 left}{t2} \fmf{boson,t=0}{vr,t2} % photon % labels \fmfv{l.d=5,l.a=180,l=$\ell^-$}{i1} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o1} \fmfv{l.d=7,l.a=110,l=LQ}{vl} \fmfv{l.d=5,l.a=15,l=$\gamma$}{t2} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \large \begin{fmfgraph*}(170,35) \fmfleft{i1,i2} \fmfright{o1,o2} \fmftop{t1,t2} % fermion lines \fmf{fermion}{i1,v1} % lepton line in \fmf{phantom,t=1.2}{v1,v} % support line \fmf{phantom,t=2.0}{v,v2} % support line \fmf{fermion}{v2,o1} % lepton line out \fmffreeze % internal quark line \fmf{fermion,l.d=6,l.s=left,label=$q$,t=1}{v1,vm} % quark line \fmf{plain,t=8}{vm,v2} % quark line % loop \fmf{boson,right=0.9,t=1}{v1,v2} % loop % photon \fmfshift{30 left}{t2} \fmf{boson,t=0}{v,t2} % photon % labels \fmfv{l.d=5,l.a=180,l=$\ell^-$}{i1} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o1} \fmfv{l.d=22,l.a=-85,l=LQ}{v1} \fmfv{l.d=5,l.a=15,l=$\gamma$}{t2} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \large \begin{fmfgraph*}(170,45) \fmfleft{i1,i2} \fmfright{o1,o2} \fmftop{t1,t2} % fermion lines \fmf{fermion}{i1,v1} % lepton line in \fmf{phantom,t=0.85}{v1,v2} \fmf{fermion}{v2,o1} % lepton line out \fmffreeze % loop top \fmf{phantom,t=1}{vtl,i2} % support left \fmf{phantom,t=0.6}{vtl,vtr} % support middle \fmf{phantom,t=1}{vtr,o2} % support right \fmf{plain,left=0.26,t=1.6}{v1,vtl} % support loop \fmf{fermion,left=0.26,t=1.6,l.d=5,label=$q$}{vtl,vtr} % fermion loop \fmf{plain,left=0.26,t=1.6}{vtr,v2} % quark loop % loop bottom \fmf{boson,right=1,t=1,label=LQ}{v1,v2} % LQ loop % photon \fmfshift{30 left}{t2} \fmf{boson,t=0}{vtr,t2} % photon % labels \fmfv{l.d=5,l.a=180,l=$\ell^-$}{i1} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o1} \fmfv{l.d=5,l.a=20,l=$\gamma$}{t2} \end{fmfgraph*} \end{fmffile}
LVF decay of a heavy leptons (muon, tau) to a three leptons through a LQ mediator.
\begin{fmffile}{feyngraph} \large \begin{fmfgraph*}(140,60) \fmfstraight \fmfleft{i1,i2,i3} \fmfright{o1,o2,o3} \fmftop{t1,t2} % fermion lines \fmf{fermion}{i1,v1} % lepton line in \fmf{fermion,l.d=6,label=$q$,t=0.75}{v1,v2} % quark line \fmf{fermion}{v2,o1} % lepton line out \fmffreeze % loop \fmf{phantom,t=1.7}{vl,i2} % support left \fmf{phantom,t=2.4}{vl,vr} % support middle \fmf{phantom,t=1.7}{vr,o2} % support right \fmf{boson,left=0.25,t=0.7}{v1,vl,vr,v2} % loop \fmffreeze % photon \fmf{phantom,t=0.9}{t1,vg} % support \fmfshift{5 right}{o2} \fmfshift{5 right}{o3} \fmf{boson,t=1,l.d=4,label=$\gamma$}{vr,vg} % photon \fmf{fermion,t=1.8}{o3,vg,o2} % fermion % labels \fmfv{l.d=5,l.a=180,l=$\ell^-$}{i1} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o1} \fmfv{l.d=5,l.a=-10,l=$\ell'^-$}{o2} \fmfv{l.d=5,l.a=20,l=$\ell'^+$}{o3} \fmfv{l.d=8,l.a=70,l=LQ}{vl} %\fmfv{l.d=5,l.a=15,l=$\gamma$}{t2} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \large \begin{fmfgraph*}(150,50) \fmfstraight \fmfleft{i1,i2,i3} \fmfright{o1,o2,o3} % fermion lines \fmf{fermion}{i1,v1} % lepton line in \fmf{phantom,t=1.2}{v1,v} % support line \fmf{phantom,t=2.0}{v,v2} % support line \fmf{fermion}{v2,o1} % lepton line out \fmffreeze % internal quark line \fmf{fermion,l.d=6,l.s=left,label=$q$,t=1}{v1,vm} % quark line \fmf{plain,t=8}{vm,v2} % quark line % loop \fmf{boson,right=0.9,t=1}{v1,v2} % loop % photon -> 2 leptons \fmf{boson,t=1,l.d=3,l.s=left,label=$\gamma$}{v,vg} % photon \fmf{fermion,t=1.6}{o3,vg,o2} % lepton lines \fmf{phantom,t=1}{i3,vg} % support line % labels \fmfv{l.d=5,l.a=180,l=$\ell^-$}{i1} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o1} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o2} \fmfv{l.d=5,l.a=0,l=$\ell'^+$}{o3} \fmfv{l.d=22,l.a=-85,l=LQ}{v1} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \large \begin{fmfgraph*}(130,100) \fmfleft{i1,i2,i3} \fmfright{o1,o2,o3} \fmftop{t1,t2} \fmfbottom{b1,b2} % fermion lines \fmf{fermion}{i2,v1} % lepton line in \fmf{phantom,t=0.9}{v1,v2} \fmf{fermion}{v2,o2} % lepton line out \fmffreeze % loop top \fmf{phantom,t=1}{vtl,i3} % support left \fmf{phantom,t=0.6}{vtl,vtr} % support middle \fmf{phantom,t=1}{vtr,o3} % support right \fmf{phantom,left=0.26,t=1.5}{v1,vtl,vtr} % support loop \fmf{fermion,left=0.26,t=1.5,label=$q$}{vtr,v2} % quark loop \fmffreeze \fmf{boson,left=0.57,t=1,l.d=3,label=LQ}{v1,vtr} % LQ loop % loop bottom \fmf{phantom,t=1}{vbl,i1} % support left \fmf{phantom,t=0.6}{vbl,vbr} % support middle \fmf{phantom,t=1}{vbr,o1} % support right \fmf{phantom,right=0.26,t=1.5}{v1,vbl,vbr} % support loop \fmf{boson,right=0.26,t=1.5,l.d=3,label=LQ}{vbr,v2} % LQ loop \fmffreeze \fmf{fermion,right=0.57,t=1,label=$q$}{v1,vbr} % quark loop % fermion %\fmfshift{10 right}{o1} %\fmfshift{10 right}{o3} \fmf{fermion,t=0}{vbr,o1} % fermion \fmf{fermion,t=0}{o3,vtr} % fermion % labels \fmfv{l.d=5,l.a=180,l=$\ell^-$}{i2} \fmfv{l.d=5,l.a=0,l=$\ell'^-$}{o2} %\fmfv{l.d=7,l.a=110,l=LQ}{vtl} \fmfv{l.d=5,l.a=-15,l=$\ell'^-$}{o1} \fmfv{l.d=5,l.a=20,l=$\ell'^+$}{o3} \end{fmfgraph*} \end{fmffile}
Ultra-peripheral lead-lead collisions
The text colors in the diagrams below are defined with the following in the preamble:
\usepackage{xcolor} \definecolor{myblue}{rgb}{.1,.1,.7} \definecolor{myred}{rgb}{.4,.1,.1} \definecolor{mylightred}{rgb}{.9,.1,.1} \definecolor{mygreen}{rgb}{.1,.6,.1} \definecolor{myorange}{rgb}{.9,.7,.2}
Measuring the anomalous momentum (g-2) of tau leptons in electron-positron (e+e-) collisions:
\Large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,100) \fmfleft{iq,im,ip} \fmfright{oq,t2,m,t1,op} % lead 1 \fmf{fermion}{ip,vp,op} \fmf{phantom,t=0.3}{ip,vp} % lead 2 \fmf{fermion}{iq,vq,oq} \fmf{phantom,t=0.3}{iq,vq} \fmf{phantom,t=0.2}{vp,vq} \fmffreeze % mediators \fmf{phantom,t=0.15}{vt1,im,vt2} \fmf{phantom,t=0.45}{vt1,vt2} \fmf{phantom,t=0.5}{vt1,t1} \fmf{phantom,t=0.5}{vt2,t2} \fmf{boson,t=0.7,label=$\gamma$,l.d=4,l.s=right}{vp,vt1} \fmf{boson,t=0.7,label=$\gamma$,l.d=3,l.s=left}{vq,vt2} \fmffreeze % taus \fmf{fermion,t=4,f=(.1,,.6,,.1)}{vt2,t2} \fmf{plain,t=1,label=\color{mygreen}$\tau$,l.s=left,f=(.1,,.6,,.1)}{vt2,vt1} \fmf{fermion,t=4,f=(.1,,.6,,.1)}{vt1,t1} % labels \fmfv{l=\strut e$^-$,l.a=160,l.d=4}{ip} \fmfv{l=\strut e$^-$,l.a=20,l.d=5}{op} \fmfv{l=\strut e$^+$,l.a=-160,l.d=4}{iq} \fmfv{l=\strut e$^+$,l.a=-20,l.d=5}{oq} \fmfv{l=\strut\color{mygreen}$\tau^+$,l.a=0,l.d=5}{t1} \fmfv{l=\strut\color{mygreen}$\tau^-$,l.a=0,l.d=5}{t2} \fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=(0.4,,0.1,,0.1)}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=4,f=(0.4,,0.1,,0.1)}{vq} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4}{vt1} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4}{vt2} \end{fmfgraph*} \end{fmffile}
Ultra-peripheral lead-lead collisions (UPC) to measure the anomalous momentum (g-2) for tau leptons:
\Large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,100) \fmfleft{iq,im,ip} \fmfright{oq,t2,m,t1,op} % lead 1 \fmf{phantom}{ip,vp,op} \fmf{phantom,t=0.3}{ip,vp} % lead 2 \fmf{phantom}{iq,vq,oq} \fmf{phantom,t=0.3}{iq,vq} \fmf{phantom,t=0.2}{vp,vq} \fmffreeze % mediators \fmf{phantom,t=0.15}{vt1,im,vt2} \fmf{phantom,t=0.45}{vt1,vt2} \fmf{phantom,t=0.5}{vt1,t1} \fmf{phantom,t=0.5}{vt2,t2} \fmf{boson,t=0.7,label=$\gamma$,l.d=4,l.s=right}{vp,vt1} \fmf{boson,t=0.7,label=$\gamma$,l.d=3,l.s=left}{vq,vt2} \fmf{double,width=1.9}{ip,vp,op} \fmf{double,width=1.9}{iq,vq,oq} \fmffreeze % taus \fmf{fermion}{vt2,t2} \fmf{plain,label=$\tau$\!,l.s=left}{vt2,vt1} \fmf{fermion}{vt1,t1} % labels \fmfv{l=\strut Pb,l.a=160,l.d=6}{ip} \fmfv{l=\strut Pb,l.a=20,l.d=5}{op} \fmfv{l=\strut Pb,l.a=-160,l.d=6}{iq} \fmfv{l=\strut Pb,l.a=-20,l.d=5}{oq} \fmfv{l=\strut$\tau^+$,l.a=10,l.d=5}{t1} \fmfv{l=\strut$\tau^-$,l.a=-10,l.d=5}{t2} \fmfv{decor.shape=circle,decor.filled=full,decor.size=4}{vt1} \fmfv{decor.shape=circle,decor.filled=full,decor.size=4}{vt2} \end{fmfgraph*} \end{fmffile}
\Large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,100) \fmfleft{iq,im,ip} \fmfright{oq,t2,m,t1,op} % lead 1 \fmf{phantom}{ip,vp,op} \fmf{phantom,t=0.3}{ip,vp} % lead 2 \fmf{phantom}{iq,vq,oq} \fmf{phantom,t=0.3}{iq,vq} \fmf{phantom,t=0.2}{vp,vq} \fmffreeze \fmfi{double,width=1.9}{vpath (__ip,__vp)} \fmfi{double,width=1.9}{vpath (__vp,__op)} \fmfi{double,width=1.9}{vpath (__iq,__vq)} \fmfi{double,width=1.9}{vpath (__vq,__oq)} % mediators \fmf{phantom,t=0.15}{vt1,im,vt2} \fmf{phantom,t=0.45}{vt1,vt2} \fmf{phantom,t=0.5}{vt1,t1} \fmf{phantom,t=0.5}{vt2,t2} \fmf{boson,t=0.7,label=$\gamma$,l.d=4,l.s=right}{vp,vt1} \fmf{boson,t=0.7,label=$\gamma$,l.d=3,l.s=left}{vq,vt2} \fmffreeze % taus \fmf{fermion,f=(.1,,.6,,.1)}{vt2,t2} \fmf{plain,label=\color{mygreen}$\tau$\!,l.s=left,f=(.1,,.6,,.1)}{vt2,vt1} \fmf{fermion,f=(.1,,.6,,.1)}{vt1,t1} % labels \fmfv{l=\strut Pb,l.a=160,l.d=6}{ip} \fmfv{l=\strut Pb,l.a=20,l.d=5}{op} \fmfv{l=\strut Pb,l.a=-160,l.d=6}{iq} \fmfv{l=\strut Pb,l.a=-20,l.d=5}{oq} \fmfv{l=\strut\color{mygreen}$\tau^+$,l.a=10,l.d=5}{t1} \fmfv{l=\strut\color{mygreen}$\tau^-$,l.a=-10,l.d=5}{t2} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=90,l.d=8}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=-90,l.d=8}{vq} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4}{vt1} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4}{vt2} \end{fmfgraph*} \end{fmffile}
\Large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,100) \fmfleft{iq,im,ip} \fmfright{oq,t2,m,t1,op} % lead 1 \fmf{phantom}{ip,vp,op} \fmf{phantom,t=0.3}{ip,vp} % lead 2 \fmf{phantom}{iq,vq,oq} \fmf{phantom,t=0.3}{iq,vq} \fmf{phantom,t=0.2}{vp,vq} \fmffreeze \fmfi{double,width=1.9}{vpath (__ip,__vp)} \fmfi{double,width=1.9}{vpath (__vp,__op)} \fmfi{double,width=1.9}{vpath (__iq,__vq)} \fmfi{double,width=1.9}{vpath (__vq,__oq)} % mediators \fmf{phantom,t=0.15}{vt1,im,vt2} \fmf{phantom,t=0.45}{vt1,vt2} \fmf{phantom,t=0.5}{vt1,t1} \fmf{phantom,t=0.5}{vt2,t2} \fmf{boson,t=0.7,label=$\gamma$,l.d=4,l.s=right}{vp,vt1} \fmf{boson,t=0.7,label=$\gamma$,l.d=3,l.s=left}{vq,vt2} \fmffreeze % taus \fmf{fermion,f=(.1,,.6,,.1)}{vt2,t2} \fmf{plain,label=\color{mygreen}$\tau$\!,l.s=left,f=(.1,,.6,,.1)}{vt2,vt1} \fmf{fermion,f=(.1,,.6,,.1)}{vt1,t1} % labels \fmfv{l=\strut Pb,l.a=160,l.d=6}{ip} \fmfv{l=\strut Pb,l.a=20,l.d=5}{op} \fmfv{l=\strut Pb,l.a=-160,l.d=6}{iq} \fmfv{l=\strut Pb,l.a=-20,l.d=5}{oq} \fmfv{l=\strut\color{mygreen}$\tau^+$,l.a=10,l.d=5}{t1} \fmfv{l=\strut\color{mygreen}$\tau^-$,l.a=-10,l.d=5}{t2} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=90,l.d=8}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=-90,l.d=8}{vq} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4, l=\large$\color{myblue}\delta a_\tau$,l.d=3,l.a=-40}{vt1} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4, l=\large$\color{myblue}\delta a_\tau$,l.d=3,l.a=40}{vt2} \end{fmfgraph*} \end{fmffile}
With a blob for new physics:
\Large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,100) \fmfleft{iq,im,ip} \fmfright{oq,t2,m,t1,op} % proton 1 \fmf{phantom}{ip,vp,op} \fmf{phantom,t=0.5}{ip,vp} % proton 2 \fmf{phantom}{iq,vq,oq} \fmf{phantom,t=0.5}{iq,vq} \fmf{phantom,t=0.2}{vp,vq} \fmffreeze \fmfi{double,width=1.9}{vpath (__ip,__vp)} \fmfi{double,width=1.9}{vpath (__vp,__op)} \fmfi{double,width=1.9}{vpath (__iq,__vq)} \fmfi{double,width=1.9}{vpath (__vq,__oq)} % mediators \fmf{phantom,t=0.15}{vt1,im,vt2} \fmf{phantom,t=0.45}{vt1,vt2} \fmf{phantom,t=0.7}{vt1,t1} \fmf{phantom,t=0.7}{vt2,t2} \fmf{boson,t=0.7,label=$\gamma$,l.d=4,l.s=right}{vp,vt1} \fmf{boson,t=0.7,label=$\gamma$,l.d=3,l.s=left}{vq,vt2} \fmffreeze % taus \fmf{fermion,f=(.1,,.6,,.1)}{vt2,t2} \fmf{plain,label=\color{mygreen}$\tau$,l.s=left,f=(.1,,.6,,.1)}{vt2,vt1} \fmf{fermion,f=(.1,,.6,,.1)}{vt1,t1} % labels \fmfv{l=\strut Pb,l.a=160,l.d=6}{ip} \fmfv{l=\strut Pb,l.a=20,l.d=5}{op} \fmfv{l=\strut Pb,l.a=-160,l.d=6}{iq} \fmfv{l=\strut Pb,l.a=-20,l.d=5}{oq} \fmfv{l=\strut\color{mygreen}$\tau^+$,l.a=10,l.d=5}{t1} \fmfv{l=\strut\color{mygreen}$\tau^-$,l.a=-10,l.d=5}{t2} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=90,l.d=8}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=-90,l.d=8}{vq} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4, l=\;\large$\color{myblue}\delta a_\tau$,l.d=5,l.a=-25}{vt1} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4, l=\;\large$\color{myblue}\delta a_\tau$,l.d=5,l.a=25}{vt2} \fmfblob{18}{vt2,vt1} \end{fmfgraph*} \end{fmffile}
UPC with neutron emission from electromagnetic dissociation (EMD):
\Large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,100) \fmfleft{iq,im,ip} \fmfright{oq,d,t2,m,t1,n,op} \fmfshift{7 right}{op} \fmfshift{7 right}{oq} \fmfshift{5 up}{op} \fmfshift{4 up}{n} \fmfshift{5 down}{oq} % lead 1 \fmf{phantom}{ip,vp,op} \fmf{phantom,t=0.4}{ip,vp} % lead 2 \fmf{phantom}{iq,vq,oq} \fmf{phantom,t=0.4}{iq,vq} \fmf{phantom,t=0.2}{vp,vq} \fmffreeze \fmf{phantom,label=\:Pb$^*$,l.s=left}{vp,vn} % excited Pb \fmf{phantom,t=0.9}{vn,op} % relaxed Pb \fmffreeze \fmf{phantom,t=0.1}{vn,n} % neutron \fmffreeze \fmfi{double,width=1.9}{vpath (__ip,__vp)} \fmfi{double,width=1.9}{vpath (__vp,__op)} \fmfi{double,width=1.3}{vpath (__vn,__n)} % neutron \fmfi{double,width=1.9}{vpath (__iq,__vq)} \fmfi{double,width=1.9}{vpath (__vq,__oq)} % mediators \fmf{phantom,t=0.15}{vt1,im,vt2} \fmf{phantom,t=0.65}{vt1,vt2} % t-channel \fmf{phantom,t=0.6}{vt1,t1} \fmf{phantom,t=0.6}{vt2,t2} \fmf{boson,t=0.7,label=$\gamma$,l.d=4,l.s=right}{vp,vt1} \fmf{boson,t=0.7,label=$\gamma$,l.d=3,l.s=left}{vq,vt2} \fmffreeze % taus \fmf{fermion,f=(.1,,.6,,.1)}{vt2,t2} \fmf{plain,label=\color{mygreen}$\tau$,l.d=4,l.s=left,f=(.1,,.6,,.1)}{vt2,vt1} \fmf{fermion,f=(.1,,.6,,.1)}{vt1,t1} % labels \fmfv{l=n$^0$,l.a=10,l.d=6}{n} % neutron \fmfv{l=\strut Pb,l.a=160,l.d=6}{ip} \fmfv{l=\strut Pb,l.a=20,l.d=5}{op} \fmfv{l=\strut Pb,l.a=-160,l.d=6}{iq} \fmfv{l=\strut Pb,l.a=-20,l.d=5}{oq} \fmfv{l=\strut\color{mygreen}$\tau^+$,l.a=10,l.d=5}{t1} \fmfv{l=\strut\color{mygreen}$\tau^-$,l.a=-10,l.d=5}{t2} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$\;\;,l.a=110,l.d=9}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=-90,l.d=8}{vq} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4}{vt1} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4}{vt2} \end{fmfgraph*} \end{fmffile}
UPC with a pair of tau leptons decaying into a muon and hadrons (“mutau” decay channel):
\Large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,100) \fmfleft{iq,im,ip} \fmfright{oq,n3,p3,p2,p1,n2,n1,m1,op} \fmfshift{8 right}{m1} \fmfshift{8 right}{n1} \fmfshift{8 right}{n2} \fmfshift{8 right}{p1} \fmfshift{8 right}{p2} \fmfshift{8 right}{p3} \fmfshift{8 right}{n3} % proton 1 \fmf{phantom}{ip,vp,op} \fmf{phantom,t=0.5}{ip,vp} % proton 2 \fmf{phantom}{iq,vq,oq} \fmf{phantom,t=0.5}{iq,vq} \fmf{phantom,t=0.2}{vp,vq} \fmffreeze \fmfi{double,width=1.9}{vpath (__ip,__vp)} \fmfi{double,width=1.9}{vpath (__vp,__op)} \fmfi{double,width=1.9}{vpath (__iq,__vq)} \fmfi{double,width=1.9}{vpath (__vq,__oq)} % mediators \fmf{phantom,t=0.05}{vt1,im,vt2} % pull left \fmf{phantom,t=0.45}{vt1,vt2} % pull together \fmf{phantom,t=0.6}{vt1,t1} \fmf{phantom,t=0.6}{vt2,t2} \fmf{phantom,t=0.5}{t1,t2} % pull together \fmf{phantom,t=0.8}{t2,oq} % pull right \fmf{phantom,t=0.8}{t1,op} % pull right \fmf{boson,t=0.7,label=$\gamma$,l.d=4,l.s=right}{vp,vt1} \fmf{boson,t=0.7,label=$\gamma$,l.d=3,l.s=left}{vq,vt2} \fmffreeze % taus \fmf{fermion,label=$\tau$,l.s=right}{vt2,t2} \fmf{plain,label=$\tau$\!,l.s=left}{vt2,vt1} \fmf{fermion,label=$\tau$,l.s=left}{vt1,t1} % tau decay 1 \fmf{plain,t=1}{p1,t2} \fmf{plain,t=1}{t2,p2} \fmf{plain,t=1}{p3,t2} \fmf{plain,t=1}{n3,t2} \fmfv{l=$\pi^\mp$,l.a=0,l.d=5}{p1} \fmfv{l=$\pi^\pm$,l.a=0,l.d=5}{p2} \fmfv{l=$\pi^\mp$,l.a=0,l.d=5}{p3} \fmfv{l=$\overline\nu_\tau$,l.a=-20,l.d=5}{n3} % tau decay 2 \fmf{plain,t=1}{t1,n1} \fmf{plain,t=1}{t1,n2} \fmf{plain,t=1}{t1,m1} \fmfv{l=$\mu^\pm$,l.a=20,l.d=5}{m1} \fmfv{l=$\nu_\tau$,l.a=0,l.d=5}{n1} \fmfv{l=$\nu_\mu$,l.a=0,l.d=5}{n2} % labels \fmfv{l=\strut Pb,l.a=160,l.d=6}{ip} \fmfv{l=\strut Pb,l.a=20,l.d=5}{op} \fmfv{l=\strut Pb,l.a=-160,l.d=6}{iq} \fmfv{l=\strut Pb,l.a=-20,l.d=5}{oq} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=90,l.d=8}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=-90,l.d=8}{vq} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4, l=\large$\color{myblue}\delta a_\tau$,l.d=3,l.a=-40}{vt1} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4, l=\large$\color{myblue}\delta a_\tau$,l.d=3,l.a=40}{vt2} \end{fmfgraph*} \end{fmffile}
\Large \begin{fmffile}{feyngraph} \begin{fmfgraph*}(150,100) \fmfleft{iq,im,ip} \fmfright{oq,n3,p3,p2,p1,n2,n1,m1,op} \fmfshift{8 right}{m1} \fmfshift{8 right}{n1} \fmfshift{8 right}{n2} \fmfshift{8 right}{p1} \fmfshift{8 right}{p2} \fmfshift{8 right}{p3} \fmfshift{8 right}{n3} % proton 1 \fmf{phantom}{ip,vp,op} \fmf{phantom,t=0.5}{ip,vp} % proton 2 \fmf{phantom}{iq,vq,oq} \fmf{phantom,t=0.5}{iq,vq} \fmf{phantom,t=0.2}{vp,vq} \fmffreeze \fmfi{double,width=1.9}{vpath (__ip,__vp)} \fmfi{double,width=1.9}{vpath (__vp,__op)} \fmfi{double,width=1.9}{vpath (__iq,__vq)} \fmfi{double,width=1.9}{vpath (__vq,__oq)} % mediators \fmf{phantom,t=0.05}{vt1,im,vt2} % pull left \fmf{phantom,t=0.45}{vt1,vt2} % pull together \fmf{phantom,t=0.6}{vt1,t1} \fmf{phantom,t=0.6}{vt2,t2} \fmf{phantom,t=0.5}{t1,t2} % pull together \fmf{phantom,t=0.8}{t2,oq} % pull right \fmf{phantom,t=0.8}{t1,op} % pull right \fmf{boson,t=0.7,label=$\gamma$,l.d=4,l.s=right}{vp,vt1} \fmf{boson,t=0.7,label=$\gamma$,l.d=3,l.s=left}{vq,vt2} \fmffreeze % taus \fmf{fermion,label=\color{mygreen}$\tau$,l.s=right,f=(.1,,.6,,.1)}{vt2,t2} \fmf{plain,label=\color{mygreen}$\tau$\!,l.s=left,f=(.1,,.6,,.1)}{vt2,vt1} \fmf{fermion,label=\color{mygreen}$\tau$,l.s=left,f=(.1,,.6,,.1)}{vt1,t1} % tau decay 1 \fmf{plain,t=1,f=(.9,,.7,,.2)}{p1,t2} \fmf{plain,t=1,f=(.9,,.7,,.2)}{t2,p2} \fmf{plain,t=1,f=(.9,,.7,,.2)}{p3,t2} \fmf{plain,t=1,f=(.1,,.6,,.1)}{n3,t2} \fmfv{l=\color{myorange}$\pi^\mp$,l.a=0,l.d=5}{p1} \fmfv{l=\color{myorange}$\pi^\pm$,l.a=0,l.d=5}{p2} \fmfv{l=\color{myorange}$\pi^\mp$,l.a=0,l.d=5}{p3} \fmfv{l=\color{mygreen}$\overline\nu_\tau$,l.a=-20,l.d=5}{n3} % tau decay 2 \fmf{plain,t=1,f=(.1,,.6,,.1)}{t1,n1} \fmf{plain,t=1,f=(.1,,.6,,.1)}{t1,n2} \fmf{plain,t=1,f=(.9,,.1,,.1)}{t1,m1} \fmfv{l=\color{mylightred}$\mu^\pm$,l.a=20,l.d=5}{m1} \fmfv{l=\color{mygreen}$\nu_\tau$,l.a=0,l.d=5}{n1} \fmfv{l=\color{mygreen}$\nu_\mu$,l.a=0,l.d=5}{n2} % labels \fmfv{l=\strut Pb,l.a=160,l.d=6}{ip} \fmfv{l=\strut Pb,l.a=20,l.d=5}{op} \fmfv{l=\strut Pb,l.a=-160,l.d=6}{iq} \fmfv{l=\strut Pb,l.a=-20,l.d=5}{oq} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=90,l.d=8}{vp} \fmfv{decor.shape=circle,decor.filled=full,decor.size=6,f=(0.4,,0.1,,0.1), l=$\color{myred}Ze$,l.a=-90,l.d=8}{vq} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4, l=\large$\color{myblue}\delta a_\tau$,l.d=3,l.a=-40}{vt1} \fmfv{decor.shape=circle,f=(0.1,,0.1,,0.7),decor.filled=full,decor.size=4, l=\large$\color{myblue}\delta a_\tau$,l.d=3,l.a=40}{vt2} \end{fmfgraph*} \end{fmffile}
Penguin diagrams
For fun, here are two alternative code snippets for the Penguin diagram from Yamanaka examples and Ohl's webpages.
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(120,120) \fmfstraight \fmfleft{g1,g2,s,dsleft,gl} \fmflabel{$\text{s}$}{s} \fmflabel{$\overline{\text{d}}$}{dsleft} \fmfright{n1,n2,d,dsright,gr} \fmflabel{$\bar \nu$}{n1} \fmflabel{$\nu$}{n2} \fmflabel{$\text{d}$}{d} \fmflabel{$\overline{\text{d}}$}{dsright} \fmf{fermion,tension=1}{dsright,dsleft} \fmf{fermion,tension=1}{s,v1} \fmf{fermion,tension=1}{v3,d} \fmf{fermion}{v1,v2} \fmf{fermion,label=$\text{t}$,label.side=right}{v2,v3} \fmf{photon,label=$\text{W}^-$,left=0.5,tension=0.2}{v1,v3} \fmf{photon,label=$\text{Z}^0$,right=0.5,tension=0.5}{v2,v4} \fmf{fermion}{n1,v4,n2} \fmf{phantom}{g1,v4,g2} \fmfv{label=$V_\text{td}$,label.angle=-35,decor.shape=circle, decor.filled=full,decor.size=2thick}{v3} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(140,120) \fmfstraight \fmfleft{x,g1,g2,x,s,dsleft,x} \fmfright{x,n1,n2,x,d,dsright,x} \fmfbottom{b} \fmflabel{$\text{b}$}{s} \fmflabel{$\text{s}$}{d} \fmf{fermion,tension=1}{dsleft,dsright} \fmf{fermion,tension=1}{s,v1} \fmf{fermion,tension=1}{v3,d} \fmf{photon,label=$\text{W}^-$,label.side=left,tension=1}{v1,v3} \fmffreeze \fmf{fermion,label=$\text{t}$,right=0.4,tension=0.2}{v1,v2} \fmf{fermion,right=0.4,label.side=right,tension=0.2}{v2,v3} \fmf{phantom,tension=0.20}{v2,b} \fmffreeze \fmf{photon,label=$\gamma/\text{Z}^0$,label.side=right,tension=0.5}{v2,v4} \fmf{fermion,tension=2}{n1,v4,n2} \fmf{phantom}{g1,v4,g2} \fmfv{label=$V_\text{ts}^{*}$,label.angle=45,label.dist=3, %decor.shape=circle, decor.filled=full,decor.size=2thick }{v3} \fmfv{label=$V_\text{tb}$,label.angle=120,label.dist=3, %decor.shape=circle, decor.filled=full,decor.size=2thick }{v1} \fmfv{label=$\ell^+$,label.angle=0}{n1} \fmfv{label=$\ell^-$,label.angle=0}{n2} \fmfv{label=$\text{$q$}$,label.angle=180}{dsleft} \fmfv{label=$\text{$q$}$,label.angle=0}{dsright} \end{fmfgraph*} \end{fmffile}
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(140,140) \fmftop{b,s} \fmfbottom{ep,em} \fmf{fermion,lab=b,lab.sid=left}{b,Vtb} \fmf{fermion,lab=s,lab.sid=left}{Vts,s} \fmf{fermion,tension=.5,lab=t,lab.sid=right}{Vtb,g,Vts} \fmf{dbl_wiggly,tension=.8,lab=W,lab.sid=left}{Vtb,Vts} \fmf{photon}{g,g'} \fmf{fermion}{ep,g',em} \fmfdot{Vtb,Vts,g,g'} \end{fmfgraph*} \end{fmffile}
As drawn by John Ellis and Melissa Franklin (explanation of the code):
\begin{fmffile}{feyngraph} \begin{fmfgraph*}(100,100) \fmfipair{Vtb,Vts,b,s,ep,em,p,p'} \fmfiequ{.5[Vtb,Vts]}{.5[nw,ne]} \fmfiequ{Vts}{Vtb+(.3w,0)} \fmfiequ{b}{.7[sw,nw]} \fmfiequ{s}{.7[se,ne]} \fmfiequ{xpart(p')}{xpart(.5[ep,em])} \fmfiequ{ypart(p')}{.2h} \fmfiequ{p}{p'+(0,.2h)} \fmfiequ{.5[ep,em]}{.5[sw,se]} \fmfiequ{em}{ep+(.7w,0)} \fmfi{dbl_wiggly,lab=W,lab.sid=right}{Vtb--Vts} \fmfi{fermion,lab=b,lab.sid=left}{b--Vtb} \fmfi{fermion,lab=s,lab.sid=left}{Vts--s} \fmfi{fermion,lab=t}{Vtb{b-Vtb} .. tension 2 .. {right}p} \fmfi{fermion,lab=t}{p{right} .. tension 2 .. {Vts-s}Vts} \fmfi{photon}{p--p'} \fmfi{fermion}{ep--p'} \fmfi{fermion}{p'--em} \fmfiv{d.sh=circle,d.siz=2thick}{Vtb} \fmfiv{d.sh=circle,d.siz=2thick}{Vts} \fmfiv{d.sh=circle,d.siz=2thick}{p} \fmfiv{d.sh=circle,d.siz=2thick}{p'} \end{fmfgraph*} \end{fmffile}