How to draw diagrams in LaTeX with TikZ

Nice looking diagrams can be drawn in LaTeX with the versatile TikZ package. This page shows some examples that are useful for our CMS group.

TikZ should work out-of-the-box with \usepackage{tikz}, but the syntax is not so straightforward at first. To get started, take a look at these materials:

Some basic shapes.
Some more basic shapes.
TeXample: A large database of simple and advanced examples with a physics section, including a Feynman diagram and a Standard Model diagram. This website will be superseded by TikZ.net.
The examples below and many more are also available on GitHub and this gallery page.
Official TikZ & PGF manual.
Visual Tikz: an extensive cheat sheet with TikZ's many features and commands.
For Feynman diagrams, please see this page.

Control regions

Control regions are simple enough to draw in TikZ, since it is in 2D and only requires to draw arrows, rectangulars and nodes (nodes are simple points, which useful for labeling). Below are two examples. The tex file containing both can be found here.

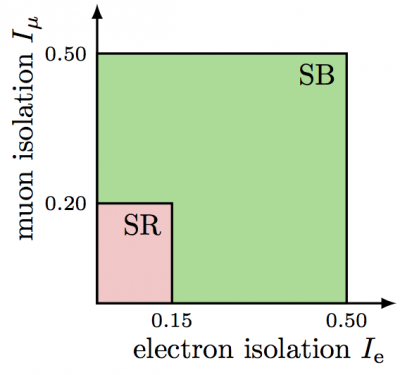
A simple example of 2D axes and colored rectangles, with custom colors defined in the preamble:

  \definecolor{mylightred}{RGB}{255,200,200}
  \definecolor{mylightblue}{RGB}{172,188,63}
  \definecolor{mylightgreen}{RGB}{150,220,150}

\begin{tikzpicture}[scale=6]
 
% define to change easily 
\def\isoe{0.15}
\def\isomu{0.20}
\def\isoSB{0.50}
\def\isomax{0.60}
 
% axes
\draw[->,thick]
  (0,0) -- (0,\isomax)
  node[at end,left=24pt,rotate=90] {muon isolation $I_\mu$};
\draw[->,thick]
  (0,0) -- (\isomax,0)
  node[at end,below=16pt,left] {electron isolation $I_\text{e}$};
 
% boxes
\draw[thick,fill=mylightgreen]
  (0,0) rectangle (\isoSB,\isoSB)
  node[anchor=north east] {SB};
\draw[thick,fill=mylightred]
  (0,0) rectangle (\isoe,\isomu)
  node[anchor=north east] {SR};
 
% labels
\draw
  (0,\isomu) node[anchor=east]  {\scriptsize$\isomu$}
  (0,\isoSB) node[anchor=east]  {\scriptsize$\isoSB$}
  (\isoe, 0) node[anchor=north] {\scriptsize$\isoe$}
  (\isoSB,0) node[anchor=north] {\scriptsize$\isoSB$};
 
\end{tikzpicture}

A simple example of a rectangle, dashed lines and using the scope environment to change the coordinate system locally in the code. In this example the coordinate system is shifted and scaled, but it also possible to do rotations (rotate=60) or scale only horizontally (vertically) with xscale=1.5 (yscale=1.5).

\begin{tikzpicture}[scale=4]
 
% axes
\draw[thick]
  (0,0) rectangle (1,1);
 
% boxes
\draw[dashed,thick]
  (0.5,-0.1) -- (0.5,1);
\draw[dashed,thick]
  (-0.1,0.5) -- (1,0.5);
 
% labels
\draw
  (0,0.75) node[anchor=east]  {OS}
  (0,0.25) node[anchor=east]  {SS}
  (0.25,0) node[anchor=north] {SR}
  (0.75,0) node[anchor=north] {SB};
\draw
  (0.25,0.75) node {QCD}
  (0.75,0.25) node[text width=40,align=center] {QCD\\shape};
 
% arrows
\begin{scope}[shift={(0.51,0.52)},scale=0.3]
  \draw[->,thick]
    (0.5,-0.5) -- (-0.5,0.5)
    node[midway, above=6pt, right=1pt] {\scriptsize$F$};
\end{scope}
 
\end{tikzpicture}

Sets

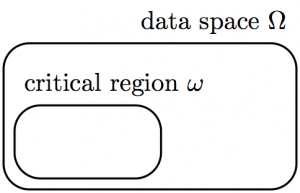
Another simple example of a rectangle with rounded corners:

sets.tex

\documentclass{article}
\usepackage{tikz}
 
% split figures into pages
\usepackage[active,tightpage]{preview}
\PreviewEnvironment{tikzpicture}
\setlength\PreviewBorder{1pt}%
 
\begin{document}
 
% SET: critical region
\begin{tikzpicture}[scale=1.0]
  \draw[black,rounded corners=10,thick]
     (0,0) rectangle (4,2)
     node[above left] {data space $\Omega$};
  \draw[black,rounded corners=10,thick,shift={(0.15,0.15)}]
    (2,0) rectangle (0,1)
     node[above right] {critical region $\omega$};
\end{tikzpicture}
 
\end{document}

Flowchart

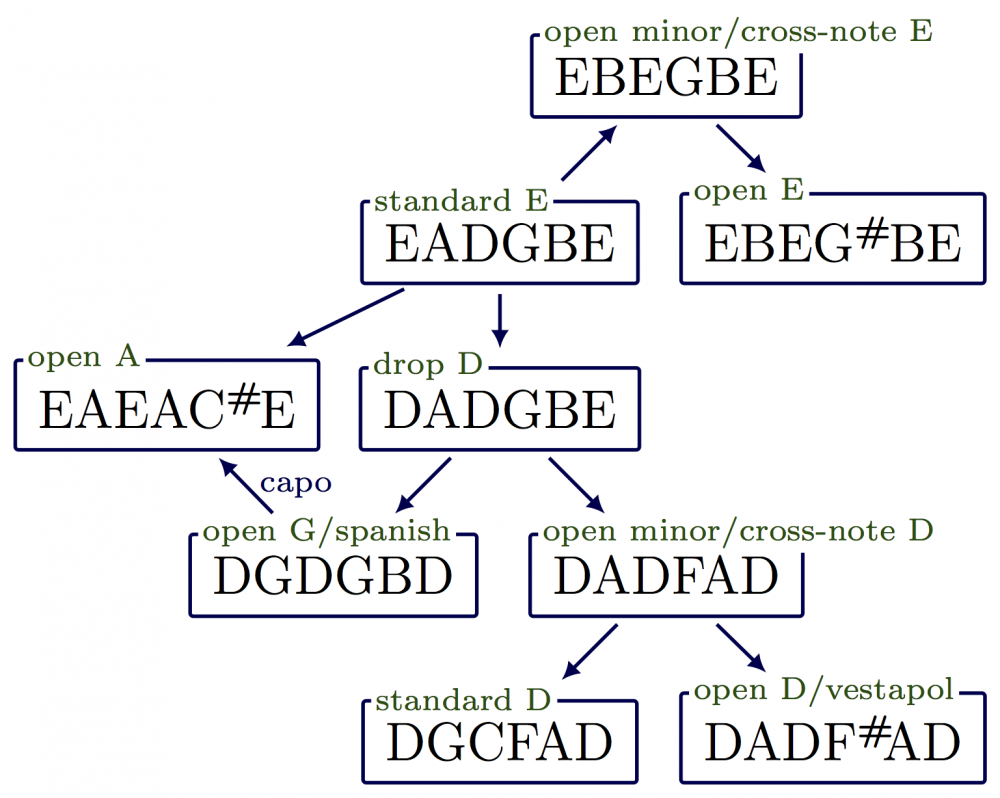
Example of a flow chart by using predefined drawing styles and a predefined box with \def and arguments (full code):

\begin{tikzpicture}[xscale=1.3,yscale=1.2,
                    fscale/.style={font=\relsize{#1}},
                    arrow/.style={->,thick,mydarkblue,shorten <=2,shorten >=4},
                    sarrow/.style={->,thick,mydarkblue,shorten <=2,shorten >=6}]
  \def\c{0.7}
  \def\m{5}
  \def\tuning(#1,#2,#3,#4,#5){
    \node[draw=mydarkblue,thick,rounded corners=\c,inner sep=\m] (#1) at (#2,#3) [fscale=1.2,anchor=south] {#4};
    \node[fill=white,inner sep=1] at (#1.north west) [fscale=-2,right=2,anchor=west,text=mydarkgreen] {#5};
  }
 
  % TUNINGS
  \tuning(E,  1, 5, EBEGBE,      open minor/cross-note E)
  \tuning(D,  0, 4, EADGBE,      standard E)
  \tuning(Dr, 2, 4, EBEG\sh\,BE, open E)
  \tuning(C,  0, 3, DADGBE,      drop D)
  \tuning(Cl,-2, 3, EAEAC\sh\,E, open A)
  \tuning(Bl,-1, 2, DGDGBD,      open G/spanish)
  \tuning(Br, 1, 2, DADFAD,      open minor/cross-note D)
  \tuning(A,  0, 1, DGCFAD,      standard D)
  \tuning(Ar, 2, 1, DADF\sh AD,  open D/vestapol)
 
  % ARROW
  \draw[sarrow,<-] (E)  -- (D);
  \draw[sarrow]    (E)  -- (Dr);
  \draw[arrow]     (D)  -- (C);
  \draw[sarrow]    (D)  -- (Cl);
  \draw[sarrow,<-] (Cl) -- (Bl) node[fscale=-2,midway,above=1,right=-2] {capo};
  \draw[sarrow]    (C)  -- (Bl);
  \draw[sarrow]    (C)  -- (Br);
  \draw[sarrow]    (Br) -- (A);
  \draw[sarrow]    (Br) -- (Ar);
 
\end{tikzpicture}

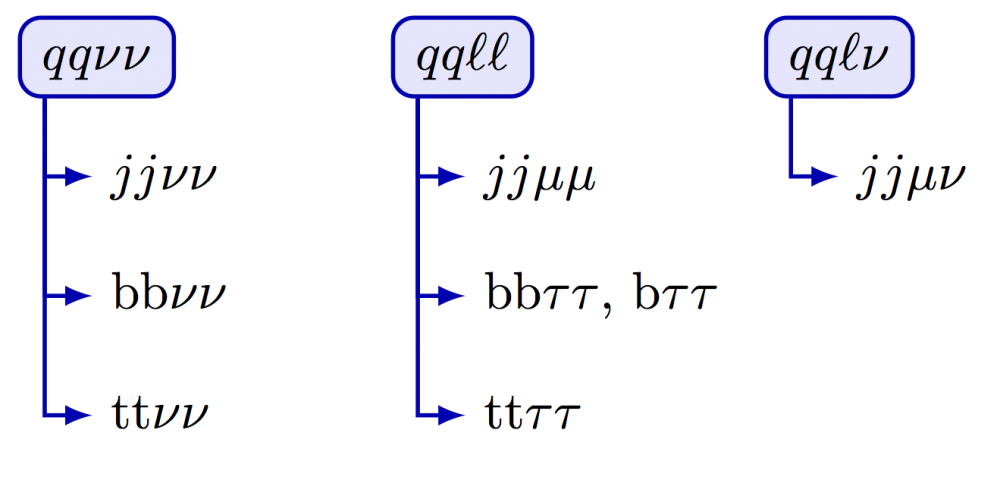
Example of a node with arrows to text below it (full code). Note the use of |- between coordinates to draw a line that first goes down vertically and then horizontally. Vice versa can be done with -|. The \strut command is used to ensure that the text line has a fixed height.

\begin{tikzpicture}[yscale=0.8,anchor=west]
 
  % FIRST COLUMN
  \node[anchor=west,draw=myblue,fill=mylightblue,thick,rounded corners=4,inner sep=1.5pt] (L) at (0,4) {\;\strut$qq\nu\nu$\;};  
  \node (L1) at (0.5,3) {\strut$jj\nu\nu$};
  \node (L2) at (0.5,2) {\strut bb$\nu\nu$};
  \node (L3) at (0.5,1) {\strut tt$\nu\nu$};
  \draw[->,myblue,thick] (L.south west)++(0.18,0) |- (L1.west);
  \draw[->,myblue,thick] (L.south west)++(0.18,0) |- (L2.west);
  \draw[->,myblue,thick] (L.south west)++(0.18,0) |- (L3.west);
 
  % SECOND COLUMN
  \begin{scope}[shift={(2.5,0)}]
    \node[draw=myblue,fill=mylightblue,thick,rounded corners=4,inner sep=1.5pt] (M) at (0,4) {\;\strut$qq\ell\ell$\;};
    \node (M1) at (0.5,3) {\strut$jj\mu\mu$};
    \node (M2) at (0.5,2) {\strut bb$\tau\tau$, b$\tau\tau$};
    \node (M3) at (0.5,1) {\strut tt$\tau\tau$};
    \draw[->,myblue,thick] (M.south west)++(0.18,0) |- (M1.west);
    \draw[->,myblue,thick] (M.south west)++(0.18,0) |- (M2.west);
    \draw[->,myblue,thick] (M.south west)++(0.18,0) |- (M3.west);
  \end{scope}
 
  % THIRD COLUMN
  \begin{scope}[shift={(5.0,0)}]
    \node[draw=myblue,fill=mylightblue,thick,rounded corners=4,inner sep=1.5pt] (R) at (0,4) {\;\strut$qq\ell\nu$\;};
    \node (R1) at (0.5,3) {\strut$jj\mu\nu$};
    \draw[->,myblue,thick] (R.south west)++(0.18,0) |- (R1.west);
  \end{scope}
 
\end{tikzpicture}

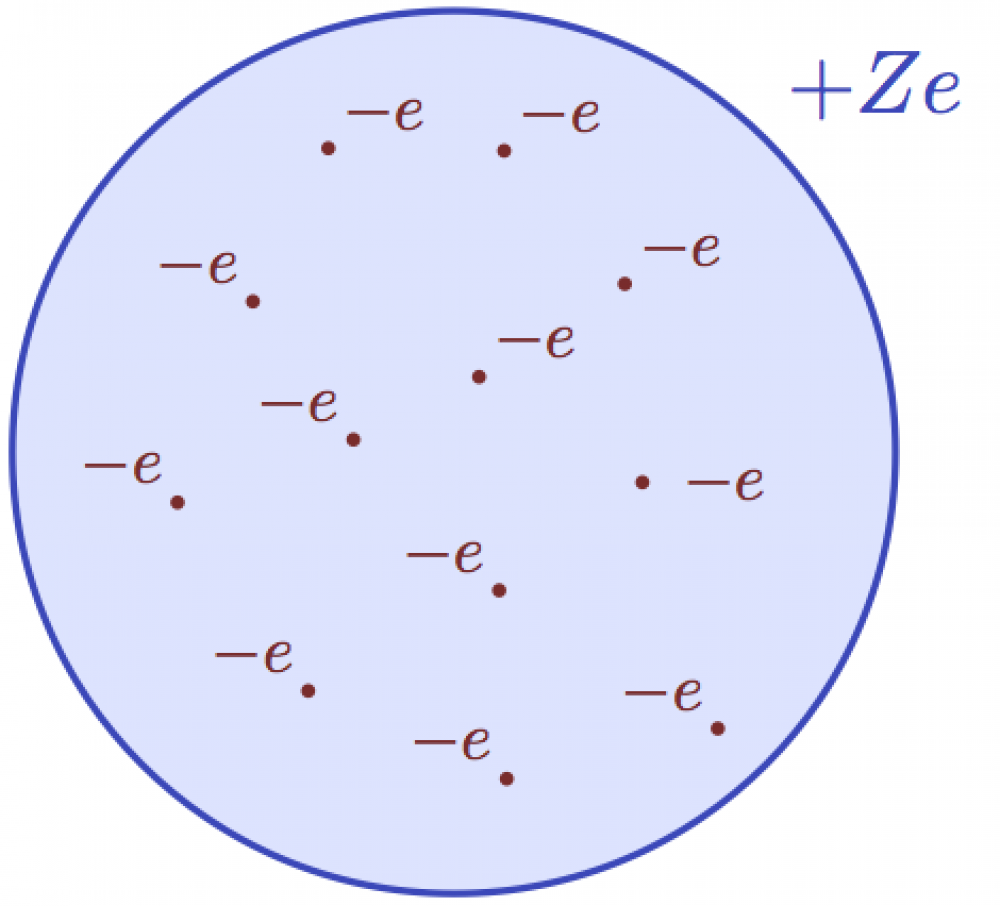
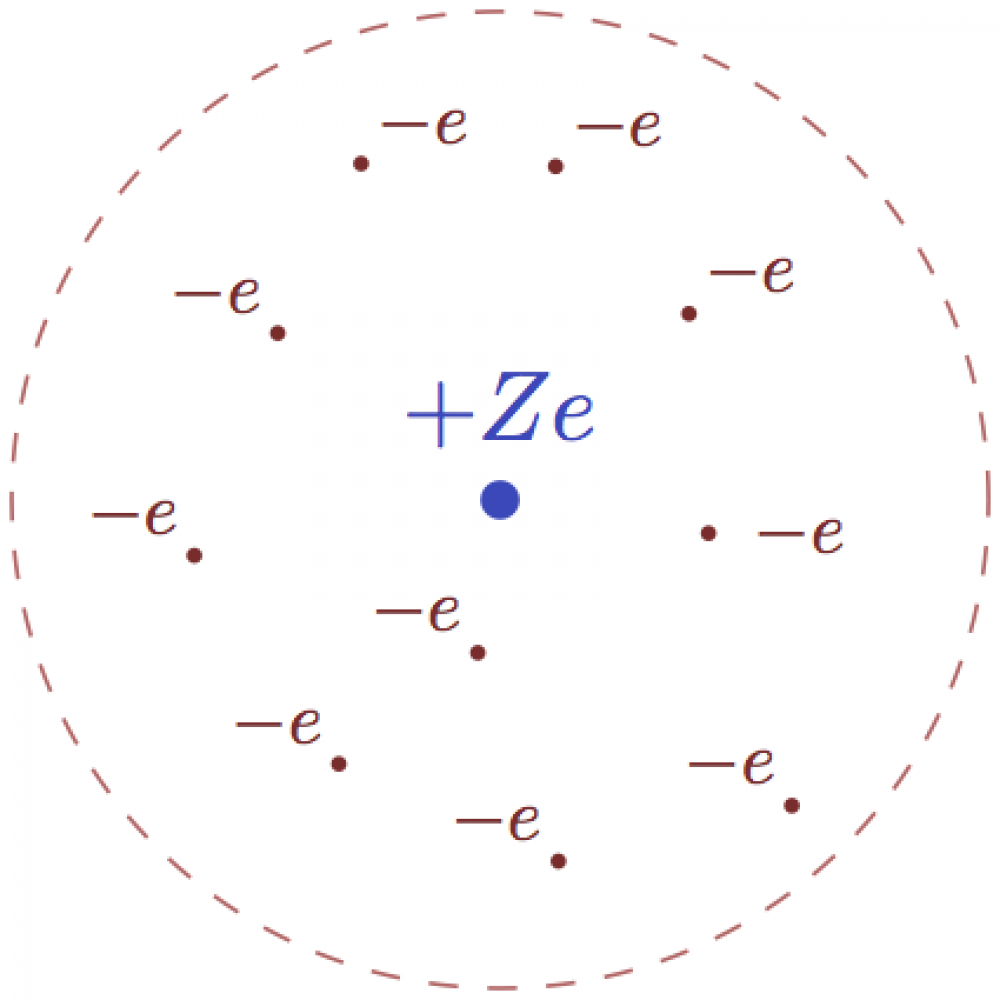
Atom models

Here are some example of making dots and circles, again with predefined colors in the preamle (see complete code for all three figures):

% colors
\definecolor{mylightred}{RGB}{255,210,210}
\definecolor{mydarkred}{RGB}{140,40,40}
\definecolor{mydarkblue}{RGB}{50,70,190}

Thomson model: uniformly and positively charged sphere with negatively charged electrons.

Simplified Rutherford model: positively charged nucleus, uniformly and negatively charged sphere.

Rutherford model: positively charged nucleus, with negatively charged “corpuscles” (electrons).

% ATOM MODEL: Simplified Rutherford model
\begin{tikzpicture}[scale=1]
  \coordinate (O)  at (0,0);
  \draw[mylightred,fill]
    (O) circle (50pt);
  \draw[mydarkred,thick]
    (O) circle (50pt) node[above right=34pt] {$-Ze$};
  \fill[radius=2.0pt,mydarkblue]
    (O) circle node[above=2pt] {$+Ze$};
\end{tikzpicture}

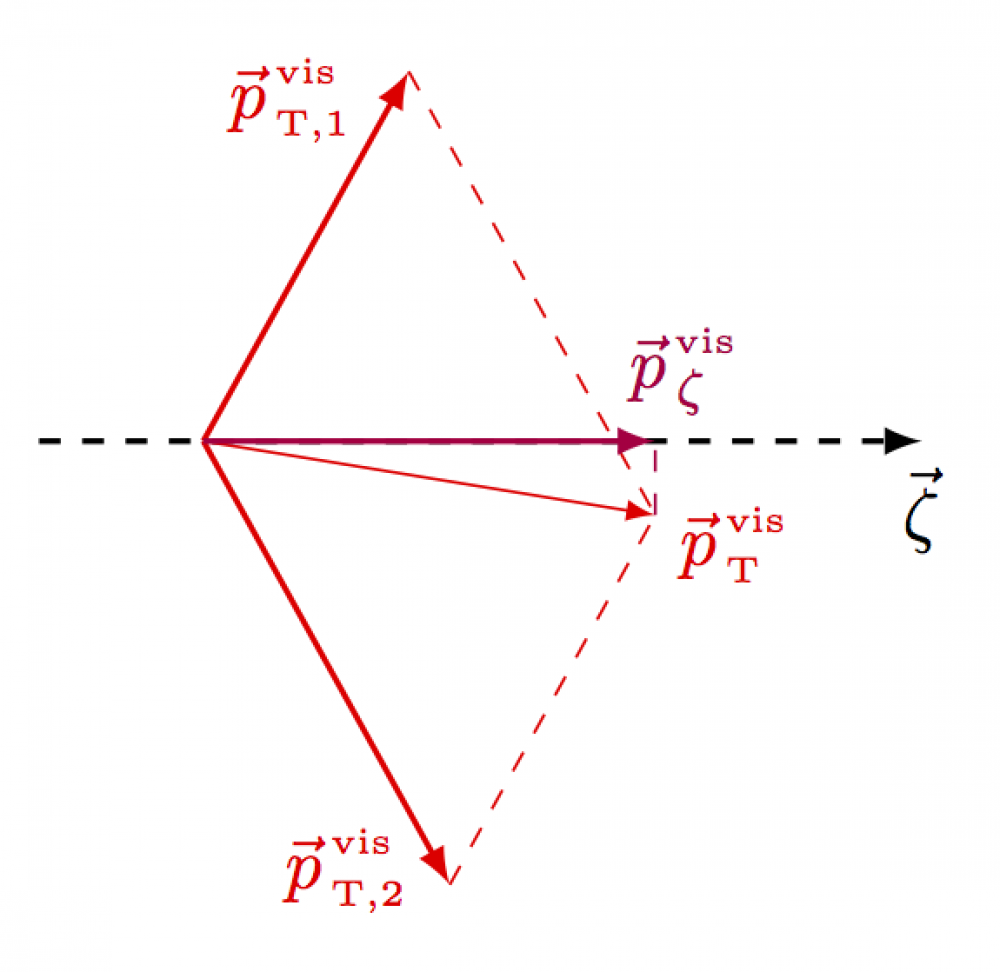
Vector sums & projections

Here is a simple example of projecting vectors, inspired by Jang (2006) [Fig. 3.5]. The tex file can be found here.

By using \coordinate, your code become more readable, and more easy to adapt with new coordinate values.

\coordinate (A) at (1,2);
\coordinate (B) at (2,-3);
\draw (A) -- (B);

In addition, you can use the TikZ library calc to do arithmetics with the coordinates, e.g.

\coordinate (AB) at ($(A)+(B)$); % (3,-1)

And you can also acces the x and y components with let \p. E.g. to define coordinate P as a projection of A onto the x-axis:

\coordinate (A)  at (1,2);
\path let \p{A}=(A) in coordinate (P) at (\x{A},0); % (1,0), projection of A

\usetikzlibrary{calc} % to sum coordinates
\begin{tikzpicture}
 
  % vector labels
  \def\pT{ \vv{p}^\text{\tiny\,vis}_\text{\tiny\,T}}
  \def\pTA{\vv{p}^\text{\tiny\,vis}_\text{\tiny\,T,1}}
  \def\pTB{\vv{p}^\text{\tiny\,vis}_\text{\tiny\,T,2}}
 
  % define point
  \coordinate (O)  at (0.0, 0.0);
  \coordinate (Z)  at (3.5, 0.0);
  \coordinate (A)  at (1.0, 1.8);
  \coordinate (B)  at (1.2,-2.16);
  \coordinate (AB) at ($(A)+(B)$);
  \path let \p{AB}=(AB) in coordinate (P) at (\x{AB},0); % projection
 
  % axis
  \draw[->,thick,dashed]
    (-0.8,0) -- (Z)
    node[at end,below] {$\vv{\zeta}$};
 
  % main vectors
  \draw[->,thick,color=red]
    (O) -- (A)
    node[below=4pt,left=4pt,color=red] {$\pTA$};
  \draw[->,thick,color=red]
    (O) -- (B)
    node[above=2pt,left=2pt,color=red] {$\pTB$};
  \draw[->,color=red]
    (O) -- (AB)
    node[below=4pt,right,color=red,scale=1] {$\pT$}; %{$\sq\pTA+\,\pTB$};
 
  % helplines
  \draw[dashed,color=red]
    (A) -- (AB);
  \draw[dashed,color=red]
    (B) -- (AB);
  \draw[dashed,color=purple]
    (AB) -- (P);
 
  % vector sum
  \draw[->,thick,color=purple]
    (O) -- (P)
    node[right=4pt,above,color=purple] {$\vv{p}^\text{\tiny\,vis}_{\tiny\,\zeta}$};
 
\end{tikzpicture}

with the predefined command

\newcommand*{\vv}[1]{\vec{\mkern0mu#1}}

in the preamble for better alignment of the vector arrow \vec over math symbols.

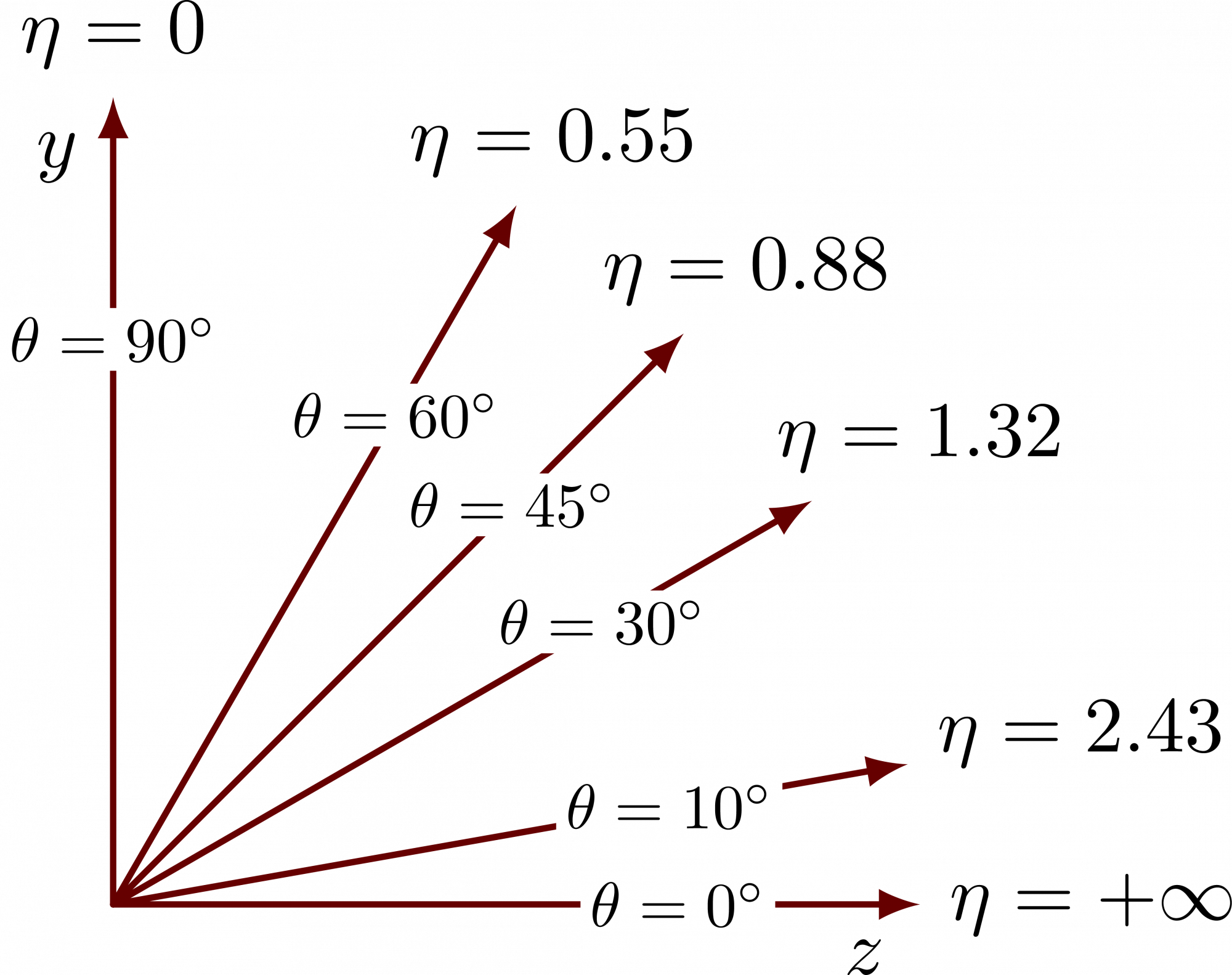
For-loops: Pseudorapidity 𝜂 and polar angle 𝜃

Here are two example of using a for-loop with TikZ's \foreach. In this case we loop over two variables. Full code can be found here.

\begin{tikzpicture}[scale=3]
 
  % limits
  \def\R{1.2}
 
  % axis labels
  \node[below=5pt,left=2pt] at (0,\R) {$y$};
  \node[left=5pt,below=2pt] at (\R,0) {$z$};
 
  % lines
  \foreach \t in {90,60,45,30,10,0}{
    \draw[->,black!60!red,thick]
      (0,0) -- ({\R*cos(\t)},{\R*sin(\t)})
      node[anchor=180+\t,black] {$\theta=\t$};
  }
 
\end{tikzpicture}

Using a for-loop over two variables:

\begin{tikzpicture}[scale=3]
 
  % limits
  \def\R{1.2} % radius/length of lines
 
  % axis labels
  \node[scale=1,below left=1] at (0,\R) {$y$}; % y axis
  \node[scale=1,below left=1] at (\R,0) {$z$}; % z axis
 
  % lines
  \foreach \t/\e in {90/0,60/0.55,45/0.88,30/1.32,10/2.43,0/+\infty}{ % loop over theta/eta
    \pgfkeys{/pgf/number format/precision=2}
    \draw[->,black!60!red,thick,line cap=round] % eta lines
      (0,0) -- (\t:\R) node[anchor=180+\t,black] {$\eta=\e$}
      node[black,pos=0.7,fill=white,scale=0.8,inner sep=1.5pt] {$\theta=\t^\circ$};
  }
 
\end{tikzpicture}

Using for-loop and calculation + rounding:

\begin{tikzpicture}[scale=3]
 
  % limits
  \def\R{1.2} % radius/length of lines
 
  % axis labels
  \node[scale=1,below left=1] at (0,\R) {$y$}; % y axis
  \node[scale=1,below left=1] at (\R,0) {$z$}; % z axis
 
  % lines
  \pgfkeys{/pgf/number format/precision=2} % two decimals
  \foreach \t in {90,60,45,30,10,0}{ % loop over theta
    \ifnum \t = 0
      \def\e{+\infty} % infinity symbol
    \else
      \pgfmathparse{-ln(tan(\t/2))} % pseudorapidity
      %\pgfmathroundto{\pgfmathresult} % round without traling zeroes
      \pgfmathroundtozerofill{\pgfmathresult} % round with trailing zeroes
      \pgfmathsetmacro\e{\t==90?0:\pgfmathresult} % no trailing zeroes for theta = 0
    \fi
    \draw[->,black!60!red,thick,line cap=round] % eta lines
      (0,0) -- (\t:\R) node[anchor=180+\t,black] {$\eta=\e$}
      node[black,pos=0.7,fill=white,scale=0.8,inner sep=1.5pt] {$\theta=\t^\circ$};
  }
 
\end{tikzpicture}

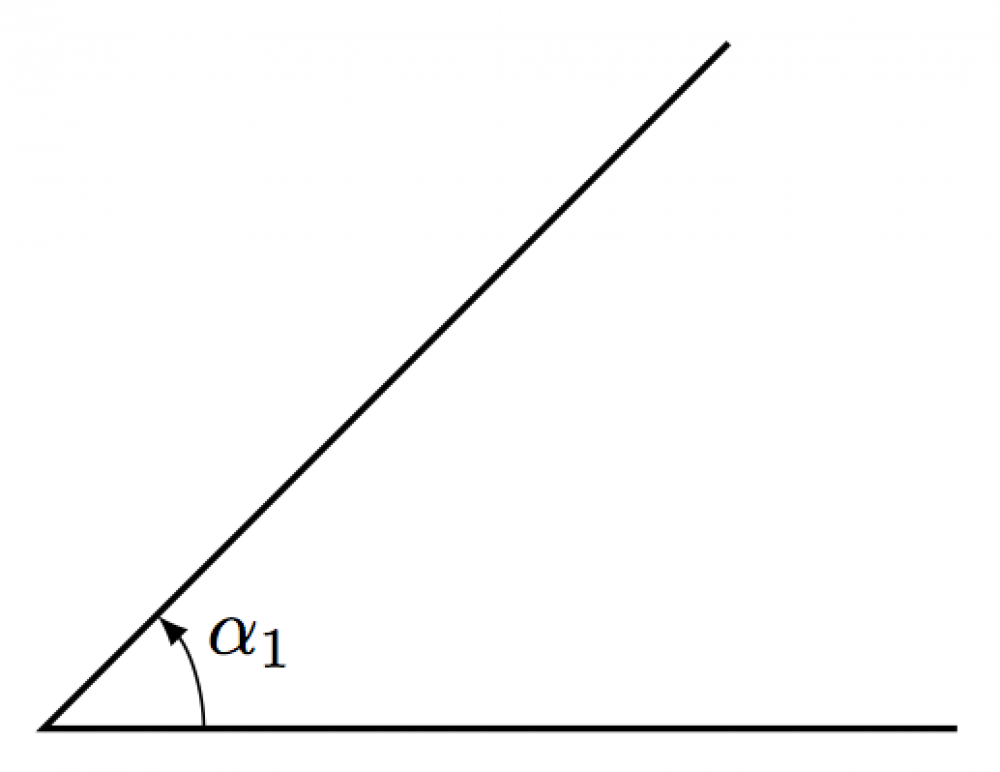
Labeling angles

Here are two different ways of labeling an angle: using \draw pic or \pic. Both give the same result and need the TikZ libraries angles and quotes.

\usetikzlibrary{angles,quotes} % for pic (angle labels)
\begin{tikzpicture}
 
  % define point
  \coordinate (A)  at (3, 3);
  \coordinate (O)  at (0, 0);
  \coordinate (B)  at (4, 0);
 
  % angle  
  \draw[thick] (A) -- (O) -- (B);
  \draw pic[->,"$\alpha_1$",draw=black,angle radius=20,angle eccentricity=1.4]
    {angle = B--O--A};
  %\pic [draw,"$\alpha_1$",angle radius=20,->,angle eccentricity=1.4]
  %  {angle = B--O--A};
 
\end{tikzpicture}

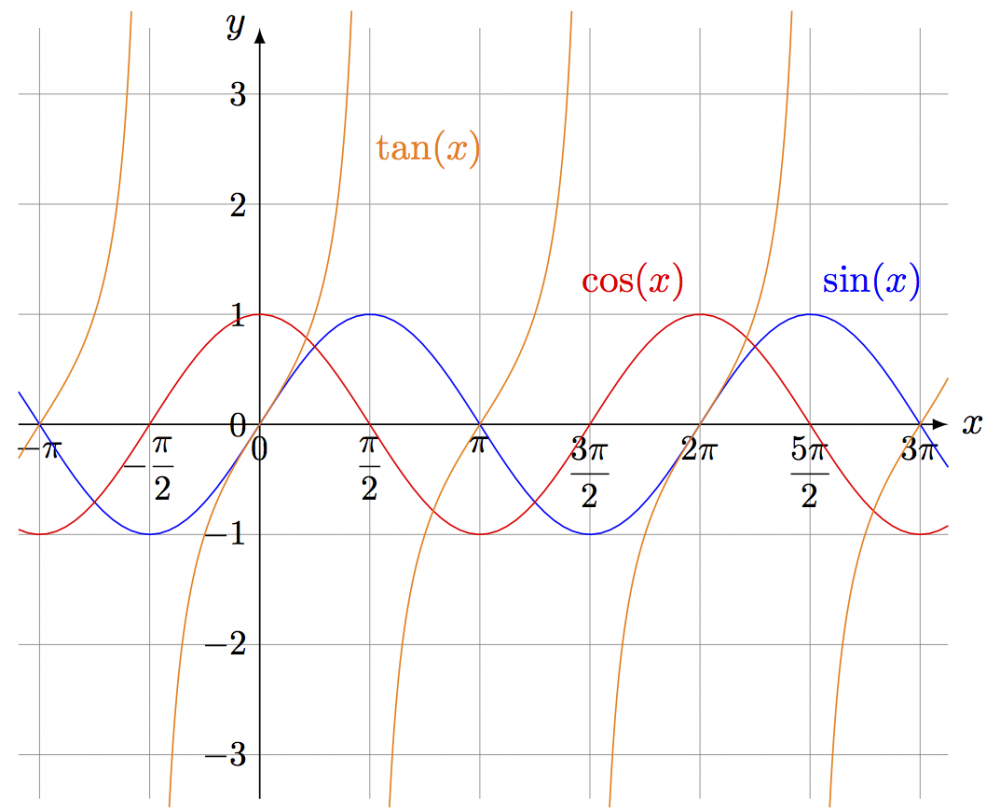
Plotting 2D functions

Examples of plotting trigonometric functions with two different methods. Full code (borrowed from a friend) can be found here.

With \draw plot(\x,{f(\x r)}) (including \usepackage{tikz} for \dfrac):

\begin{tikzpicture}[domain=-pi:pi,xscale=2/pi]
 
  % limits
  \def\xa{ -pi-0.3}
  \def\xb{3*pi+0.4}
  \def\ya{-3.4}
  \def\yb{ 3.6}
  \def\N{100} % number of points
 
  % axes & grid
  \draw[xstep=pi/2,very thin, color=gray]
    (\xa,\ya) grid (\xb,\yb);
  \draw[->]
    (\xa,0) -- (\xb,0)
    node[right] {$x$};
  \draw[->]
    (0,\ya) -- (0,\yb)
    node[left] {$y$};
 
  % ticks
  \draw[] % x
  	node[below,scale=0.9] at ( -pi,   0) {$-\pi$}
  	node[below,scale=0.9] at ( -pi/2, 0) {$-\dfrac{\pi}{2}$}
  	node[below,scale=0.9] at (  pi,   0) {$\pi$}
  	node[below,scale=0.9] at (     0, 0) {0}
  	node[below,scale=0.9] at (  pi/2, 0) {$\dfrac{\pi}{2}$}
  	node[below,scale=0.9] at (  pi,   0) {$\pi$}
  	node[below,scale=0.9] at (3*pi/2, 0) {$\dfrac{3\pi}{2}$}
  	node[below,scale=0.9] at (2*pi,   0) {$2\pi$}
  	node[below,scale=0.9] at (5*pi/2, 0) {$\dfrac{5\pi}{2}$}
  	node[below,scale=0.9] at (3*pi,   0) {$3\pi$};
  \draw[] % y
  	node[left,scale=0.9] at ( 0,  3) {$3$}
  	node[left,scale=0.9] at ( 0,  2) {$2$}
  	node[left,scale=0.9] at ( 0,  1) {$1$}
  	node[left,scale=0.9] at ( 0,  0) {$0$}
  	node[left,scale=0.9] at ( 0, -1) {$-1$}
  	node[left,scale=0.9] at ( 0, -2) {$-2$}
  	node[left,scale=0.9] at ( 0, -3) {$-3$};
 
  % function
  \def\ea{0.28}
  \def\eb{0.26}
  \draw[color=blue,samples=\N,domain=\xa:\xb] % SIN
    plot(\x,{sin(\x r)}) % r for radians
    node[above right] at (5*pi/2,1) {$\sin(x)$};
  \draw[color=red,samples=\N,domain=\xa:\xb] % COS
    plot(\x,{cos(\x r)})
    node[above left] at (2*pi,1) {$\cos(x)$};
  \draw[color=orange] % TAN
    plot[samples=\N,domain=  \xa     :   -pi/2-\eb] (\x, {tan(\x r)})
    plot[samples=\N,domain=  -pi/2+\ea:   pi/2-\eb] (\x, {tan(\x r)})
    plot[samples=\N,domain=   pi/2+\ea: 3*pi/2-\eb] (\x, {tan(\x r)})
    plot[samples=\N,domain= 3*pi/2+\ea: 5*pi/2-\eb] (\x, {tan(\x r)})
    plot[samples=\N,domain= 5*pi/2+\ea:  \xb      ] (\x, {tan(\x r)})
    node[samples=\N,right=-2pt] at (pi/2,2.5) {$\tan(x)$};
 
\end{tikzpicture}

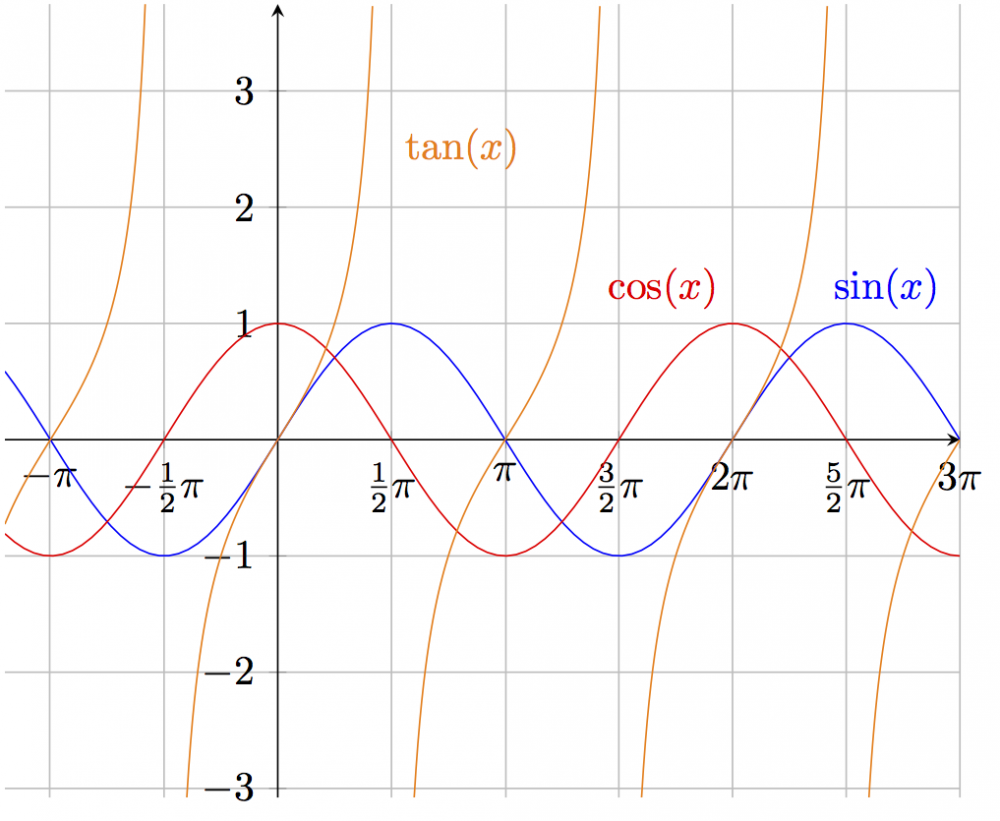
With \addplot in the axis environment.

\begin{tikzpicture}[scale=1.2]
\begin{axis}[enlargelimits=false,
             axis lines=middle,
             scale=1.2,
             xtick={-3.15159, -1.57080, 0,
                     1.57080,  3.15159, 4.71239,
                     6.28318,  7.85398, 9.42478 }, 
             xticklabels={$-\pi$, $-\frac{1}{2}\pi$, 0,
                          $\frac{1}{2}\pi$, $\pi$, $\frac{3}{2}\pi$,
                          $2\pi$, $\frac{5}{2}\pi$, $3\pi$ },
             ytick={-3,-2,-1,0,1,2,3},
             grid=major, % only a grid on the defined ticks
             samples=100 % number of points
             ]
 
  % sin
  \addplot[blue,no marks,domain=-1.2*pi:3*pi]{sin(deg(x))}; % deg to convert radians
  \node[right=10pt,above] at (axis cs:5*pi/2,1){\color{blue}$\sin(x)$};
 
  % cos
  \addplot[red,no marks,domain=-1.2*pi:3*pi] {cos(deg(x))};
  \node[above left] at (axis cs:2*pi,1){\color{red}$\cos(x)$};
 
  % tan, multiple parts because of singularities
  \addplot[orange,no marks,domain=-1.2*pi:-0.583*pi, ]{tan(deg(x))};
  \addplot[orange,no marks,domain=-0.4*pi:5*pi/12,   ]{tan(deg(x))};
  \addplot[orange,no marks,domain=27*pi/45:17*pi/12, ]{tan(deg(x))};
  \addplot[orange,no marks,domain=1.6*pi:29*pi/12,   ]{tan(deg(x))};
  \addplot[orange,no marks,domain=2.6*pi:36*pi/12,   ]{tan(deg(x))};
  \node[right] at (axis cs:pi/2,2.5){\color{orange}$\tan(x)$};
 
\end{axis}
\end{tikzpicture}

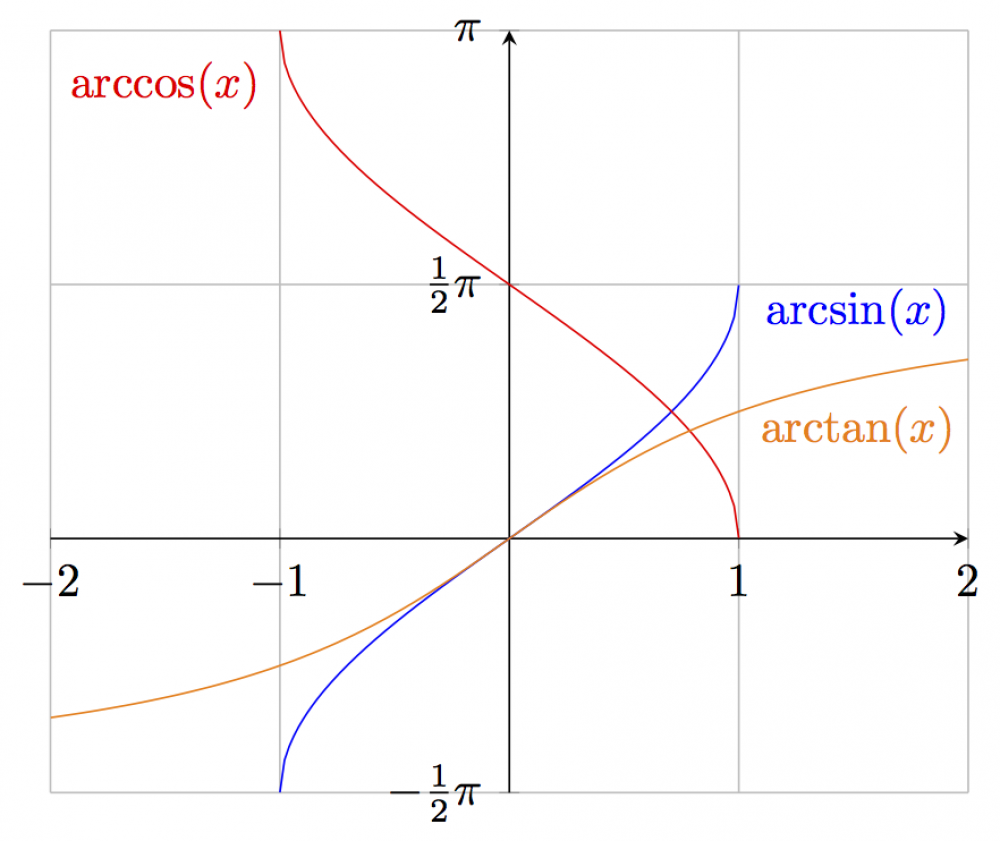
\begin{tikzpicture}
\begin{axis}[enlargelimits=false,
             axis lines=middle,
             xtick={-2,-1,0,1,2},
             ytick={-1.570780, 1.570780, 3.14159},
             yticklabels={$-\frac{1}{2}\pi$,$\frac{1}{2}\pi$,$\pi$},
             grid=major,
             samples=100
             ]
 
  % arcsin
  \addplot[domain=-1:1,no marks,blue] {rad(asin(x))};
  \node at (axis cs:1.52,1.4){\color{blue}$\arcsin(x)$};
 
  % arccos
  \addplot[domain=-1:1,no marks,red] {rad(acos(x))};
  \node at (axis cs:-1.5,2.8){\color{red}$\arccos(x)$};
 
  % arctan
  \addplot[domain=-2:2,no marks,orange] {rad(atan(x))};
  \node at (axis cs:1.52,.67){\color{orange}$\arctan(x)$};
 
\end{axis}
\end{tikzpicture}

Full code:

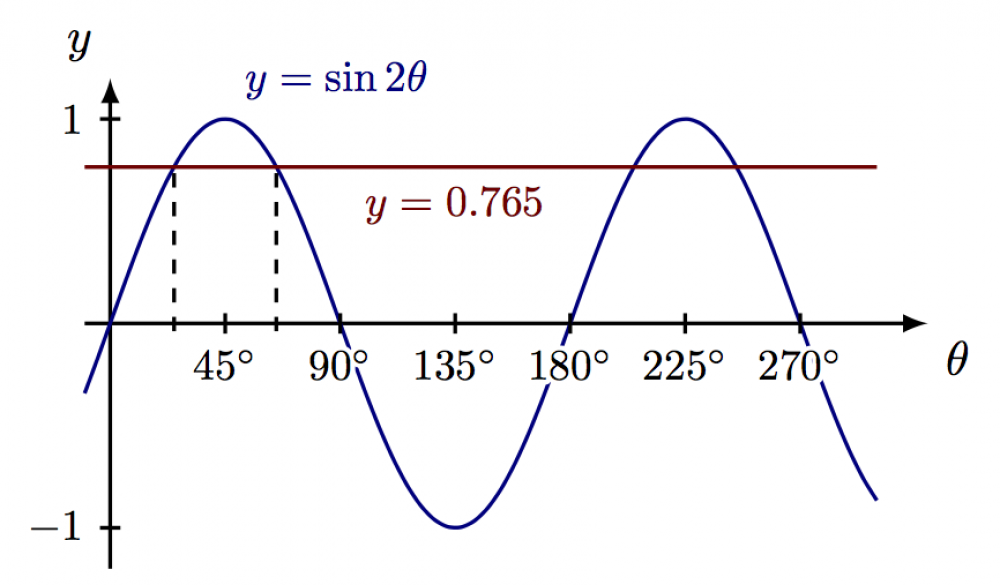
\begin{tikzpicture}[scale=1.5,xscale=1/80]
 
  \def\N{60}
  \def\xmin{-10}  \def\xmax{320}
  \def\ymin{-1.2} \def\ymax{1.2}
  \def\tmin{-10}  \def\tmax{300}
  \def\blue{black!50!blue}, \def\red{black!50!red}
  \def\value{0.765}
  \def\Dtheta{20}
 
  % axes
  \draw[->,thick]
    (\xmin,0) -- (\xmax,0)
    node[anchor=north west] {$\theta$};
  \draw[->,thick]
    (0,\ymin) -- (0,\ymax)
    node[anchor=south east] {$y$};
 
  % plots
  \draw[thick,\blue,variable=\t,domain=\tmin:\tmax,samples=\N,smooth]
    plot (\t,{sin(2*\t)});
  \draw[thick,\red,variable=\t,domain=\tmin:\tmax,samples=\N,smooth]
    plot (\t,\value);
 
  % function labels
  \node[\blue,above right=1pt,scale=0.9] at (45,1) {$y=\sin2\theta$};
  \node[\red, below=1pt,scale=0.9] at (135,\value) {$y=\value$};
 
  % numerical solutions
  \draw[dashed,thick] (45-\Dtheta,-\value*0.05) -- (45-\Dtheta,\value*1.05);
  \draw[dashed,thick] (45+\Dtheta,-\value*0.05) -- (45+\Dtheta,\value*1.05);
 
  % ticks
  \foreach \x in {45,90,135,180,225,270}{
    \draw[thick]
      (\x,0.05) -- (\x,-0.05) node[below,scale=0.9] {\contour{white}{$\x^\circ$}};}
  \foreach \y in {1,-1}{
    \draw[thick]
      (4,\y) -- (-4,\y) node[left,scale=0.9] {$\y$};}
 
\end{tikzpicture}

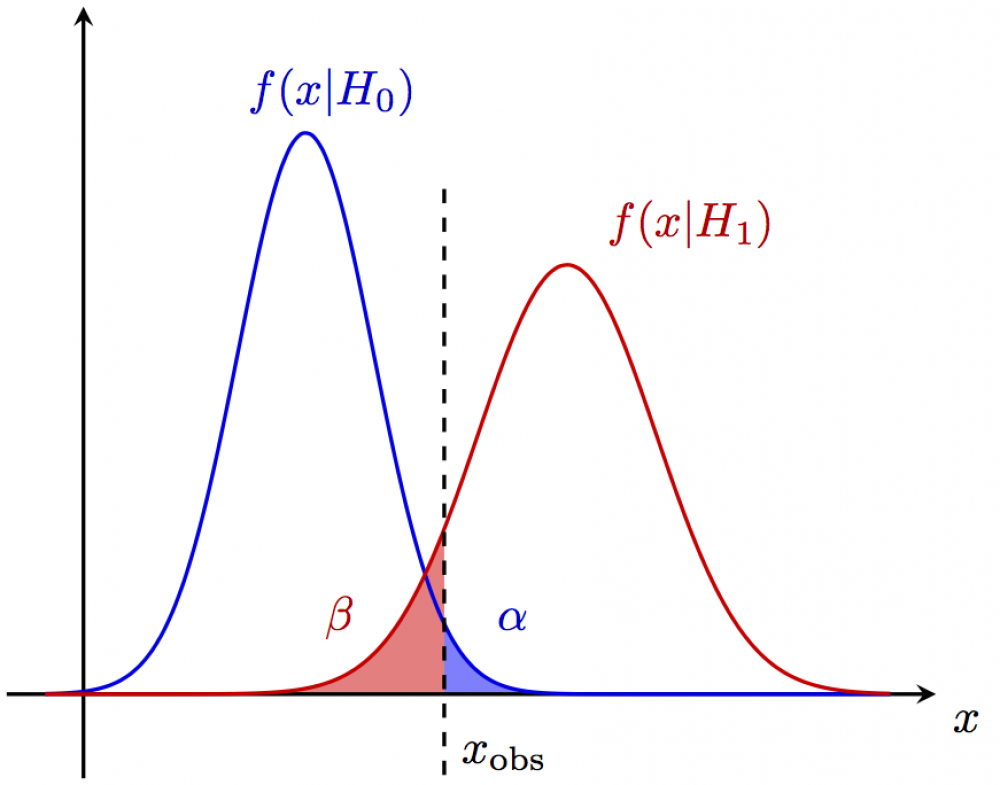
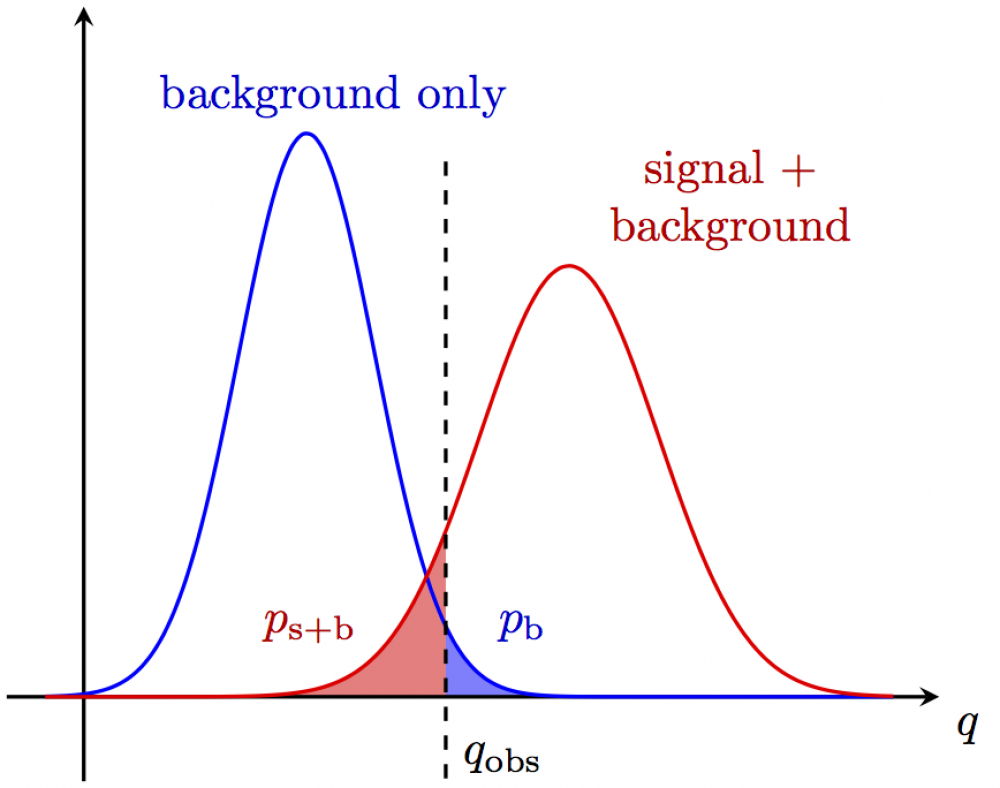
Here is an example from statistics, using the pgfplots library fillbetween to make a shaded area between a function and a path. The full code can be found here. The gauss function is defined as

\pgfmathdeclarefunction{gauss}{3}{%
  \pgfmathparse{1/(#3*sqrt(2*pi))*exp(-((#1-#2)^2)/(2*#3^2))}%
}

% GAUSSIANs
\begin{tikzpicture}
 
  \def\q{13.8};
  \def\B{8.5};
  \def\S{18.5};
  \def\Bs{2.60};
  \def\Ss{3.40};
  \def\xmax{\S+3.2*\Ss};
  \def\ymin{{-0.15*gauss(\B,\B,\Bs)}};
 
  \begin{axis}[every axis plot post/.append style={
               mark=none,domain={-0.05*(\xmax)}:{1.08*\xmax},samples=80,smooth},
               xmin={-0.1*(\xmax)}, xmax=\xmax,
               ymin=\ymin, ymax={1.1*gauss(\B,\B,\Bs)},
               axis lines=middle,
               axis line style=thick,
               enlargelimits=upper, % extend the axes a bit to the right and top
               ticks=none,
               xlabel=$x$,
               every axis x label/.style={at={(current axis.right of origin)},anchor=north west},
              ]
 
    % plots
    \addplot[name path=B,thick,black!10!blue] {gauss(x,\B,\Bs)};
    \addplot[name path=S,thick,black!10!red ] {gauss(x,\S,\Ss)};
    \addplot[black,dashed,name path=Q,thick]
      coordinates {(\q, {0.90*gauss(\B,\B,\Bs)}) (\q, \ymin)}
      node[below=2pt,anchor=south west] {$x_\text{obs}$};
 
    % fill
    \path[name path=xaxis]
      (0,0) -- (\xmax,0);
    \addplot[white!50!blue] fill between[of=xaxis and B, soft clip={domain=\q:\xmax}];
    \addplot[white!50!red]  fill between[of=xaxis and S, soft clip={domain=0:\q}];
 
    % labels
    \node[above,      black!20!blue] at (1.12*\B,{gauss(\B,\B,\Bs)}) {$f(x|H_0)$};
    \node[above right,black!20!red ] at (1.05*\S,{gauss(\S,\S,\Ss)}) {$f(x|H_1)$};
    \node[above left, black!20!red ] at ({0.8*\q},{gauss(1.07*\q,\B,\Bs)}) {\strut$\beta$};
    \node[above right,black!20!blue] at ({1.1*\q},{gauss(1.07*\q,\B,\Bs)}) {\strut$\alpha$};
 
  \end{axis}
\end{tikzpicture}

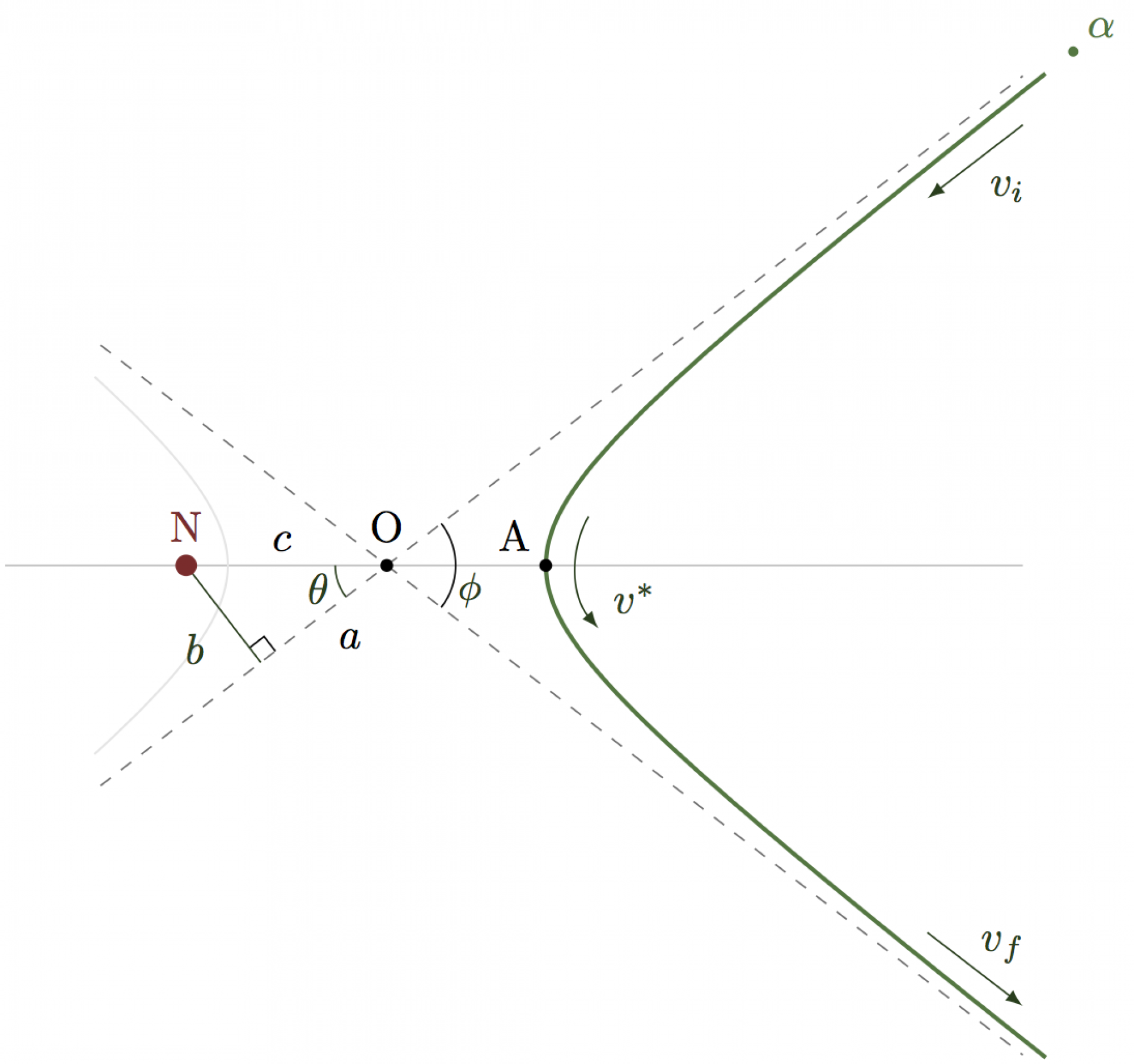
Plotting 2D parametrized functions: Rutherford scattering

Example of a hyperbolic orbit in Rutherford scattering of an 𝛼-particle off a nucleus with parametrized functions.

\def\a{1}
\def\b{2}
\def\N{100}
\draw[samples=\N,variable=\t,domain=-2:2]
    plot({-\a*cosh(\t)},{\b*sinh(\t)});

Full code can be found here.

Plotting 3D functions

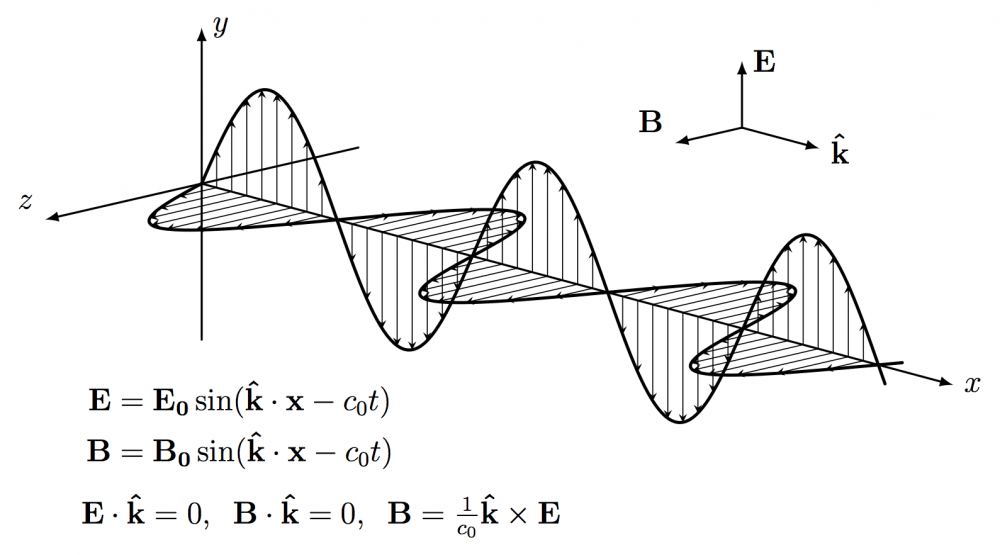
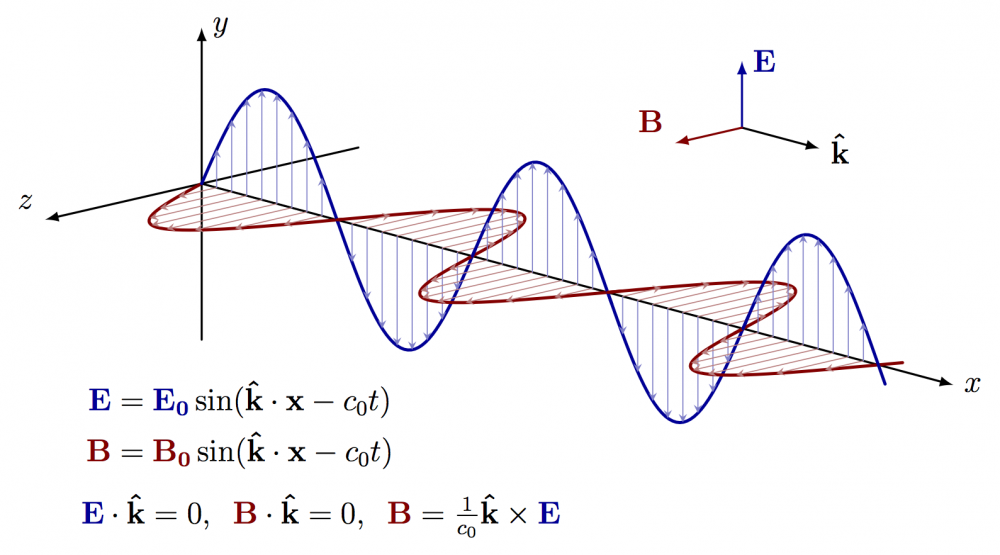
Examples of plotting trigonometric functions in 3D (full code).

\begin{tikzpicture}[x=(-15:1.2), y=(90:1.0), z=(-150:1.0),
                    line cap=round, line join=round,
                    axis/.style={black, thick,->},
                    vector/.style={>=stealth,->}]
  \large
  \def\A{1.5}
  \def\nNodes{5} % use even number
  \def\nVectorsPerNode{8}
  \def\N{\nNodes*40}
  \def\xmax{\nNodes*pi/2*1.01}
  \pgfmathsetmacro\nVectors{(\nVectorsPerNode+1)*\nNodes}
 
  \def\vE{\mathbf{E}}
  \def\vB{\mathbf{B}}
  \def\vk{\mathbf{\hat{k}}}
 
  \draw[very thick,variable=\t,domain=0:\nNodes*pi/2*1.01,samples=\N]
    plot (\t,{\A*sin(\t*360/pi)},0);
  \draw[very thick,variable=\t,domain=0:\nNodes*pi/2*1.01,samples=\N]
    plot (\t,0,{\A*sin(\t*360/pi)});
 
  % main axes
  \draw[axis] (0,0,0) -- ++(\xmax*1.1,0,0) node[right] {$x$};
  \draw[axis] (0,-\A*1.4,0) -- (0,\A*1.4,0) node[right] {$y$};
  \draw[axis] (0,0,-\A*1.4) -- (0,0,\A*1.4) node[above left] {$z$};
 
  % ...
 
\end{tikzpicture}

3D axis with spherical coordinates & CMS coordinate system

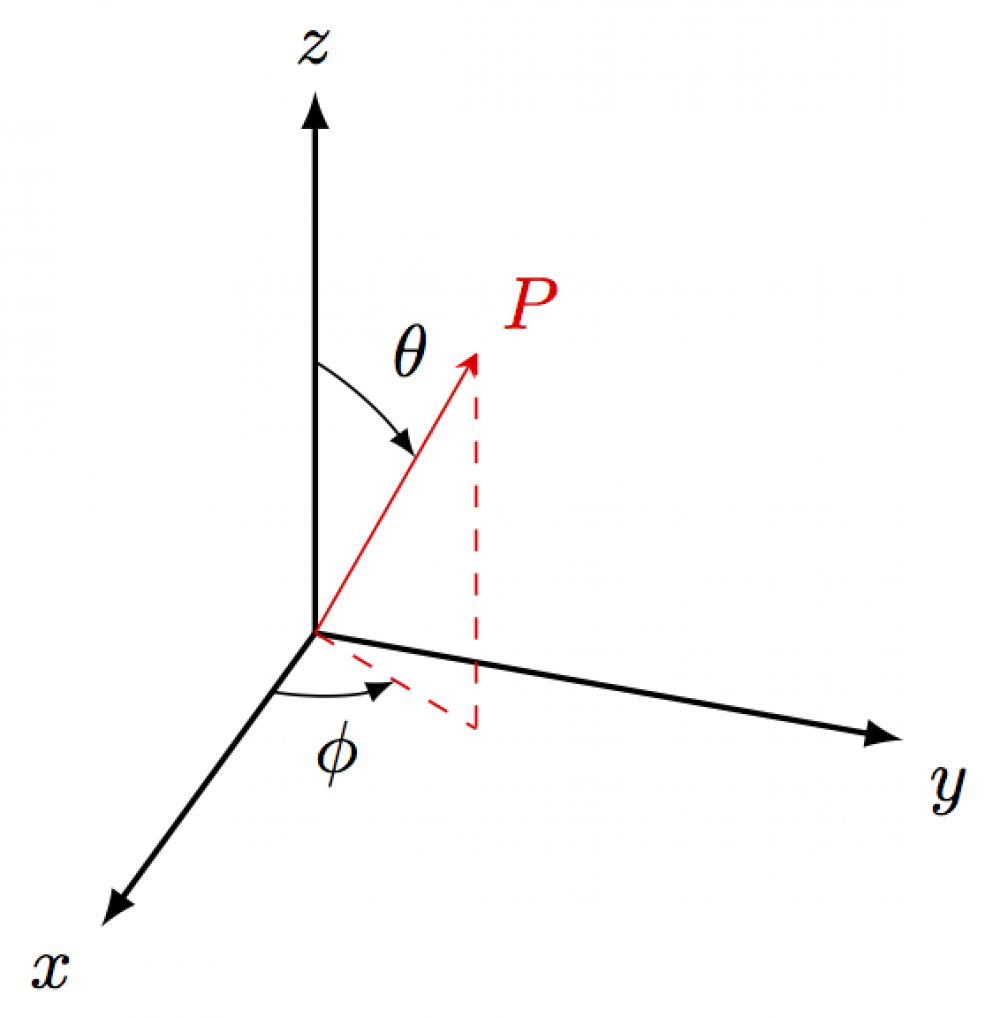
This piece of code is based on this StackExchange thread. It is a simple exercise in making axes and labeling angles in 3D. \usepackage{tikz-3dplot} needs to be included. The full code can be found here.

\tdplotsetmaincoords{60}{110}
\begin{tikzpicture}[scale=3,tdplot_main_coords]
 
  % variables
  \def\rvec{.8}
  \def\thetavec{30}
  \def\phivec{60}
 
  % axes & vector
  \coordinate (O) at (0,0,0);
  \draw[thick,->] (0,0,0) -- (1,0,0) node[anchor=north east]{$x$};
  \draw[thick,->] (0,0,0) -- (0,1,0) node[anchor=north west]{$y$};
  \draw[thick,->] (0,0,0) -- (0,0,1) node[anchor=south]{$z$};
  \tdplotsetcoord{P}{\rvec}{\thetavec}{\phivec}
    \draw[-stealth,color=red] (O) -- (P) node[above right] {$P$};
 
  % arcs
  \draw[dashed, color=red] (O) -- (Pxy);
  \draw[dashed, color=red] (P) -- (Pxy);
  \tdplotdrawarc[->]{(O)}{0.2}{0}{\phivec}
    {anchor=north}{$\phi$}
  \tdplotsetthetaplanecoords{\phivec}
  \tdplotdrawarc[->,tdplot_rotated_coords]{(0,0,0)}{0.5}{0}{\thetavec}
    {anchor=south west}{$\theta$}
 
\end{tikzpicture}

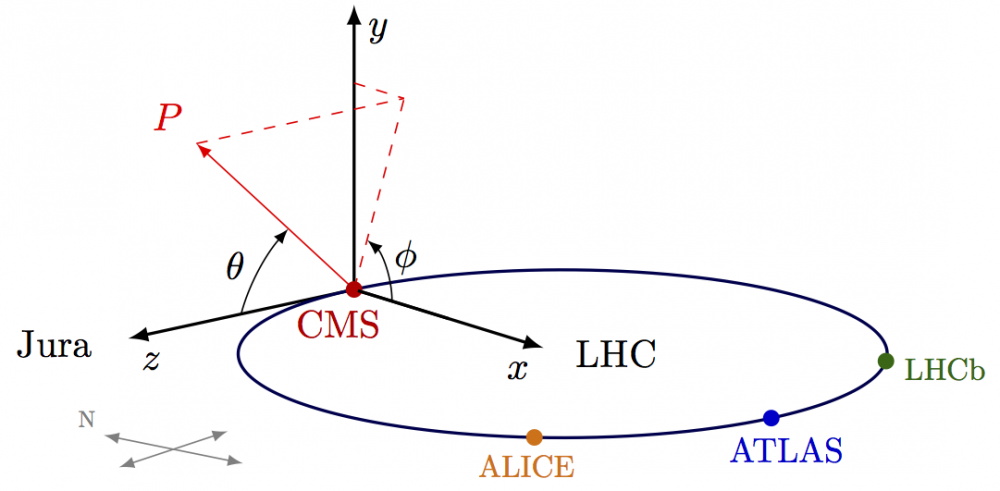
An example of rotating the 3D axes with the CMS conventional coordinate system by using the option rotate around x=<angle> and more (full code):

% CMS conventional coordinate system with LHC and other detectors
\tdplotsetmaincoords{75}{50} % to reset previous setting
\begin{tikzpicture}[scale=2.7,tdplot_main_coords,rotate around x=90]
 
  % variables
  \def\rvec{1.2}
  \def\thetavec{40}
  \def\phivec{70}
  \def\R{1.1}
  \def\w{0.3}
 
  % axes
  \coordinate (O) at (0,0,0);
  \draw[thick,->] (0,0,0) -- (1,0,0) node[below left]{$x$};
  \draw[thick,->] (0,0,0) -- (0,1,0) node[below right]{$y$};
  \draw[thick,->] (0,0,0) -- (0,0,1) node[below right]{$z$};
  \tdplotsetcoord{P}{\rvec}{\thetavec}{\phivec}
 
  % vectors
  \draw[->,red] (O) -- (P) node[above left] {$P$};
  \draw[dashed,red] (O)  -- (Pxy);
  \draw[dashed,red] (P)  -- (Pxy);
  \draw[dashed,red] (Py) -- (Pxy);
 
  % circle - LHC
  \tdplotdrawarc[thick,rotate around x=90,black!70!blue]{(\R,0,0)}{\R}{0}{360}{}{}
 
  % compass - the line between CMS and ATLAS has a ~12° declination (http://googlecompass.com)
  \begin{scope}[shift={(1.1*\R,0,1.65*\R)},rotate around y=12]
    \draw[<->,black!50] (-\w,0,0) -- (\w,0,0);
    \draw[<->,black!50] (0,0,-\w) -- (0,0,\w);
    \node[above left,black!50,scale=0.6] at (-\w,0,0) {N};
  \end{scope}
 
  % nodes
  \node[left,align=center] at (0,0,1.1) {Jura};
  \node[right] at (\R,0,0) {LHC};
  \fill[radius=0.8pt,black!20!red]
    (O) circle node[left=4pt,below=2pt] {CMS};
  \draw[thick] (0.02,0,0) -- (0.5,0,0); % partially overdraw x-axis and CMS point
  \fill[radius=0.8pt,black!20!blue]
    (2*\R,0,0) circle
    node[right=4pt,below=2pt,scale=0.9] {ATLAS};
  \fill[radius=0.8pt,black!10!orange]
    ({\R*sqrt(2)/2+\R},0,{ \R*sqrt(2)/2}) circle % 45 degrees from ATLAS
    node[left=2pt,below=2pt,scale=0.8] {ALICE};
  \fill[radius=0.8pt,black!60!green]
    ({\R*sqrt(2)/2+\R},0,{-\R*sqrt(2)/2}) circle % 45 degrees from ATLAS
    node[below=2pt,right=2pt,scale=0.8] {LHCb};
 
  % arcs
  \tdplotdrawarc[->]{(O)}{0.2}{0}{\phivec}
    {above=2pt,right=-1pt,anchor=mid west}{$\phi$}
  \tdplotdrawarc[->,rotate around z=\phivec-90,rotate around y=-90]{(0,0,0)}{0.5}{0}{\thetavec}
    {anchor=mid east}{$\theta$}
 
\end{tikzpicture}

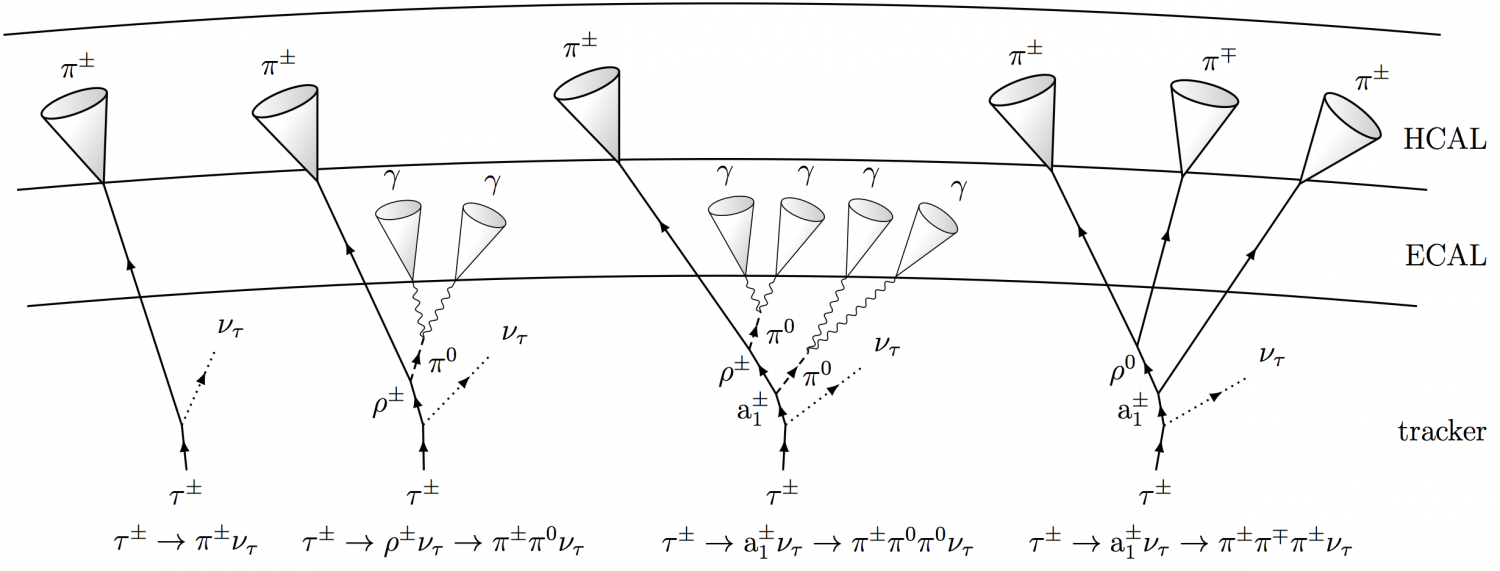
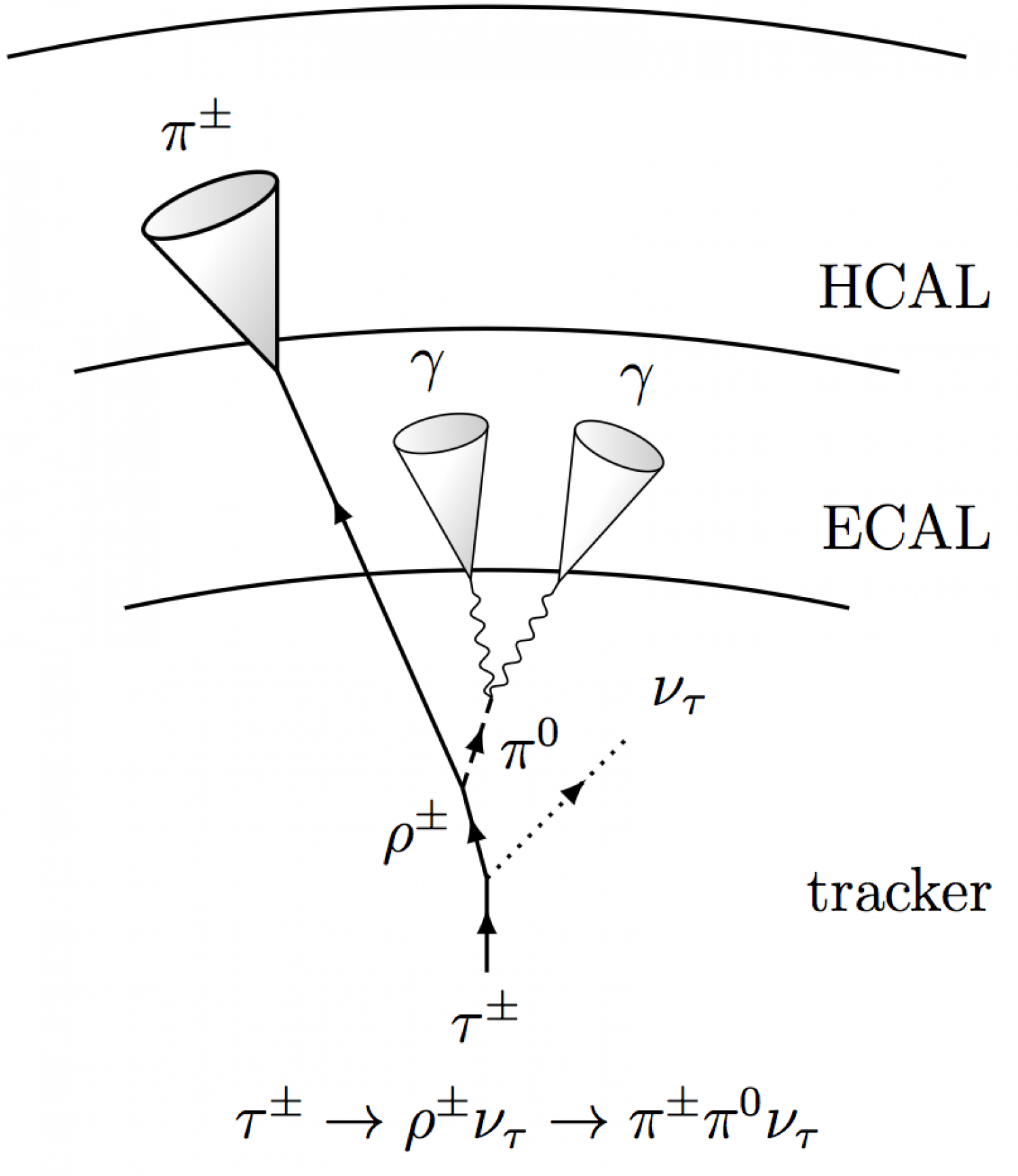
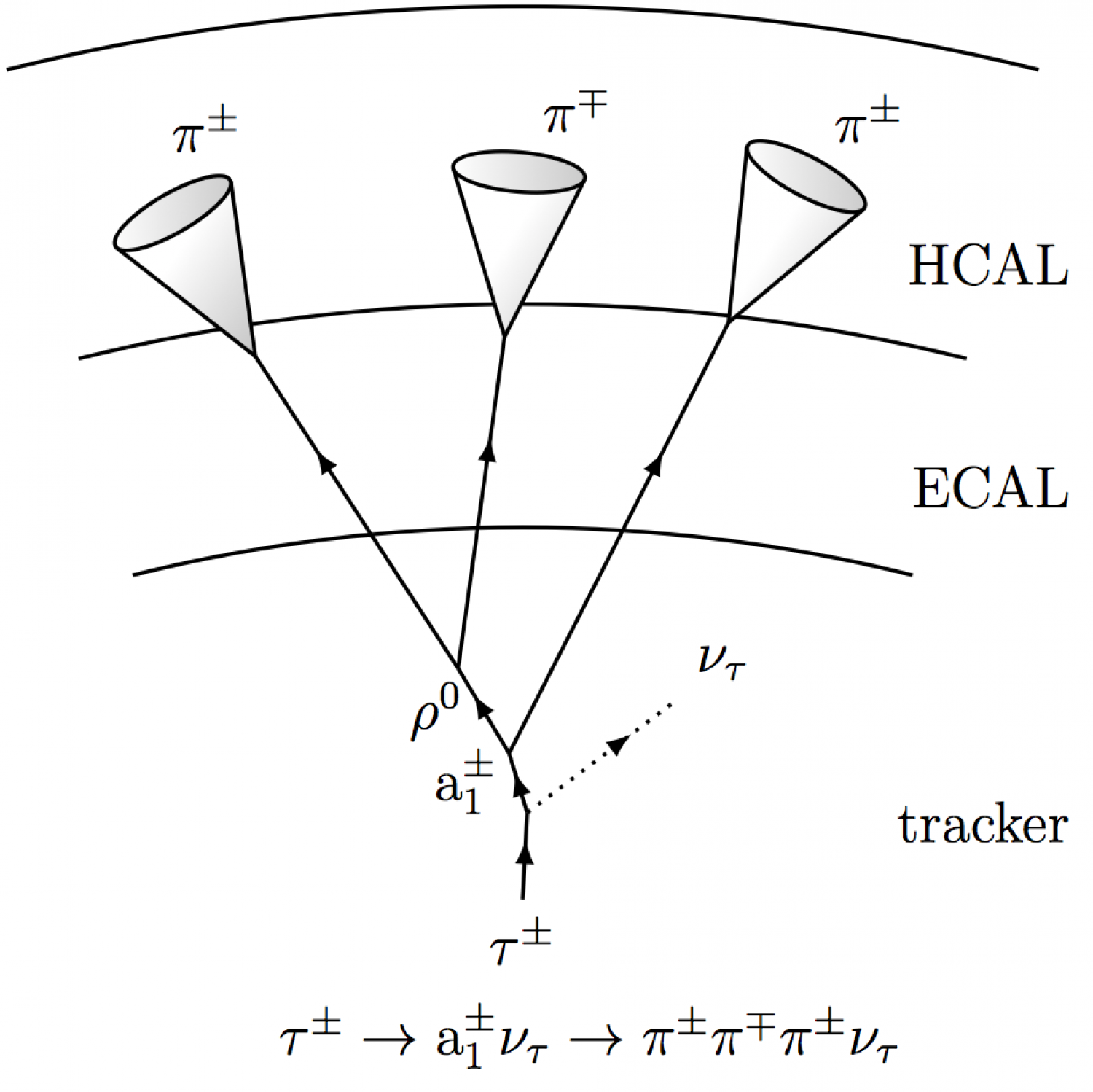
Tau lepton decay signatures

Inspiration from Takahashi & Tomoto (2012) [Fig. 3.14, p. 37]. Full code.

Physics exercise

Oscillating mass (full code).

Falling object (full code).

Thrown object (full code).

Solenoid (full code).

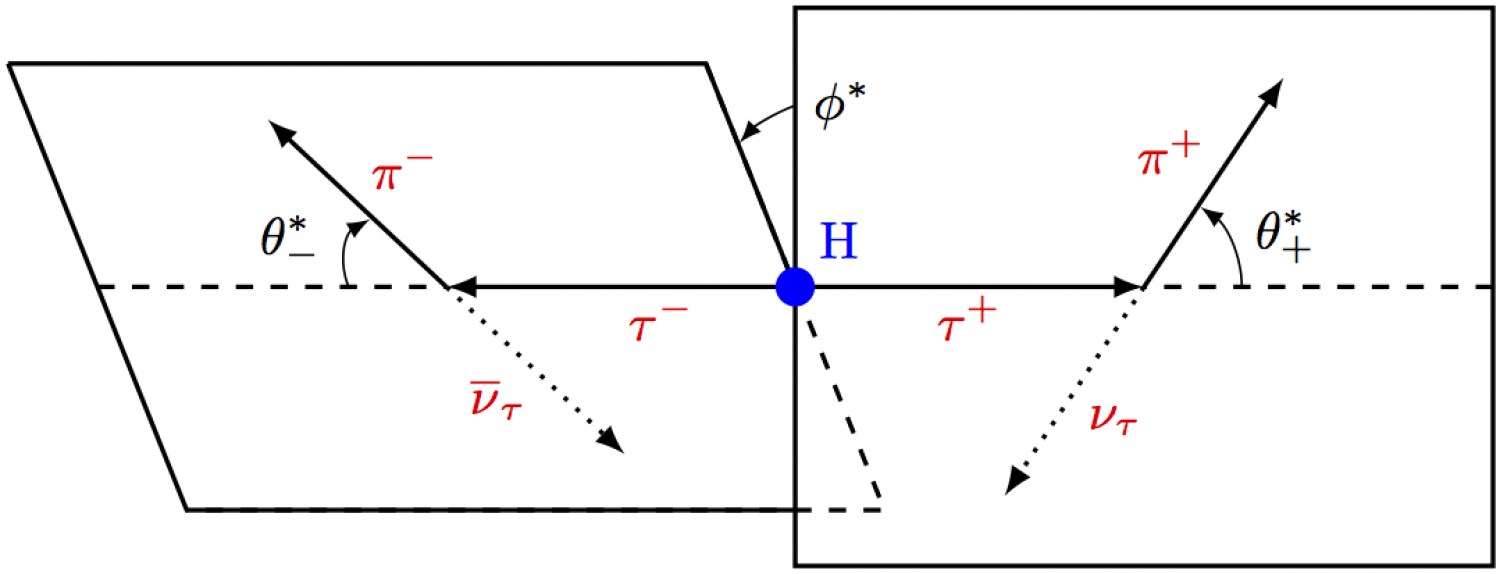
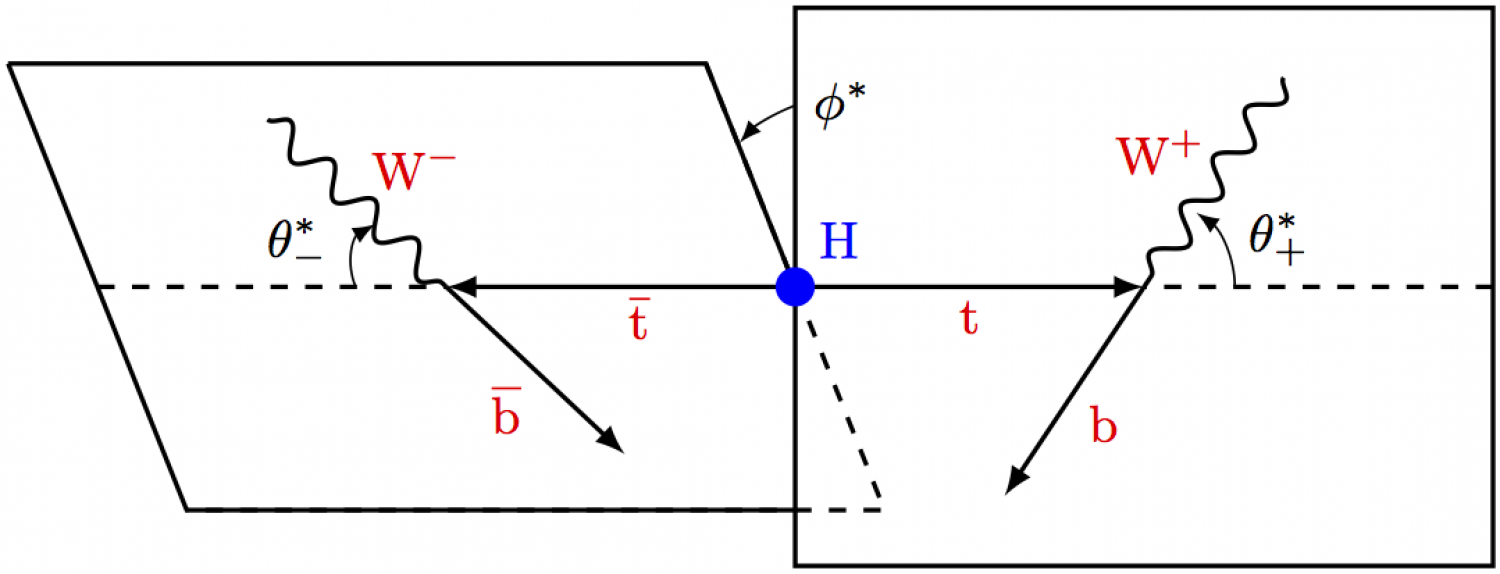
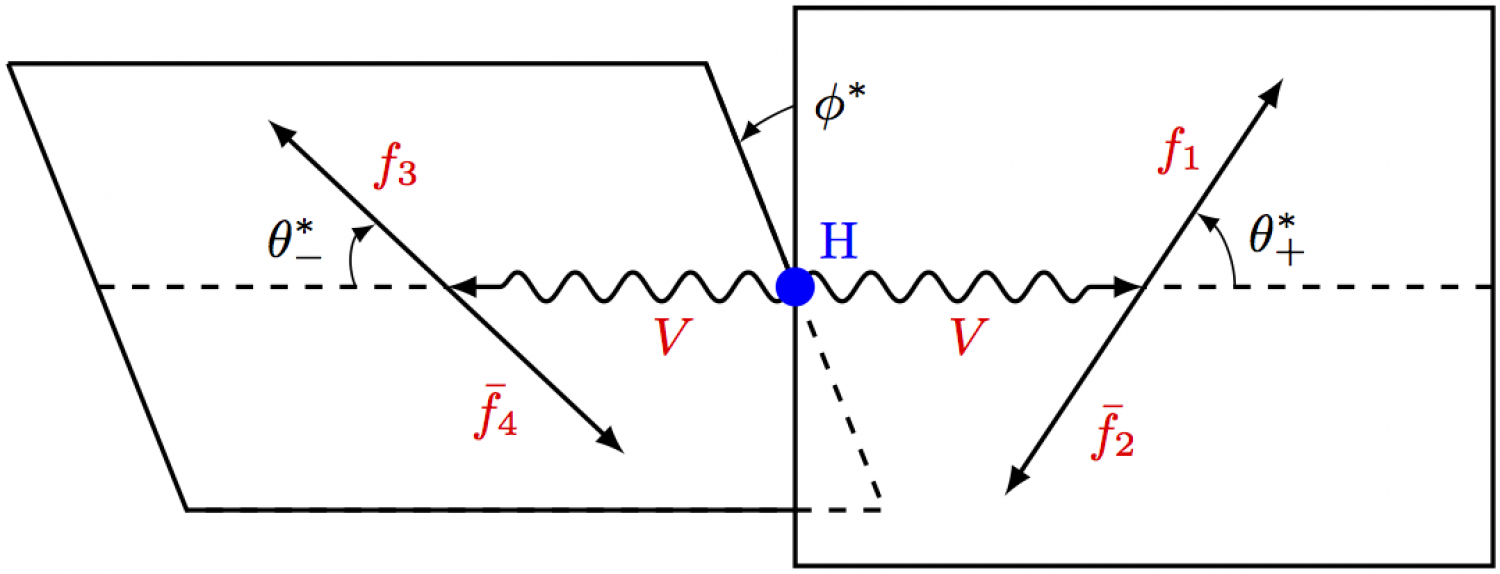
Higgs decay planes

Decay planes of Higgs decay to measure the Higgs boson's parity. The full code can be found here. Adaptation of Djouadi (2008) [Fig. 2.6, 2.11].

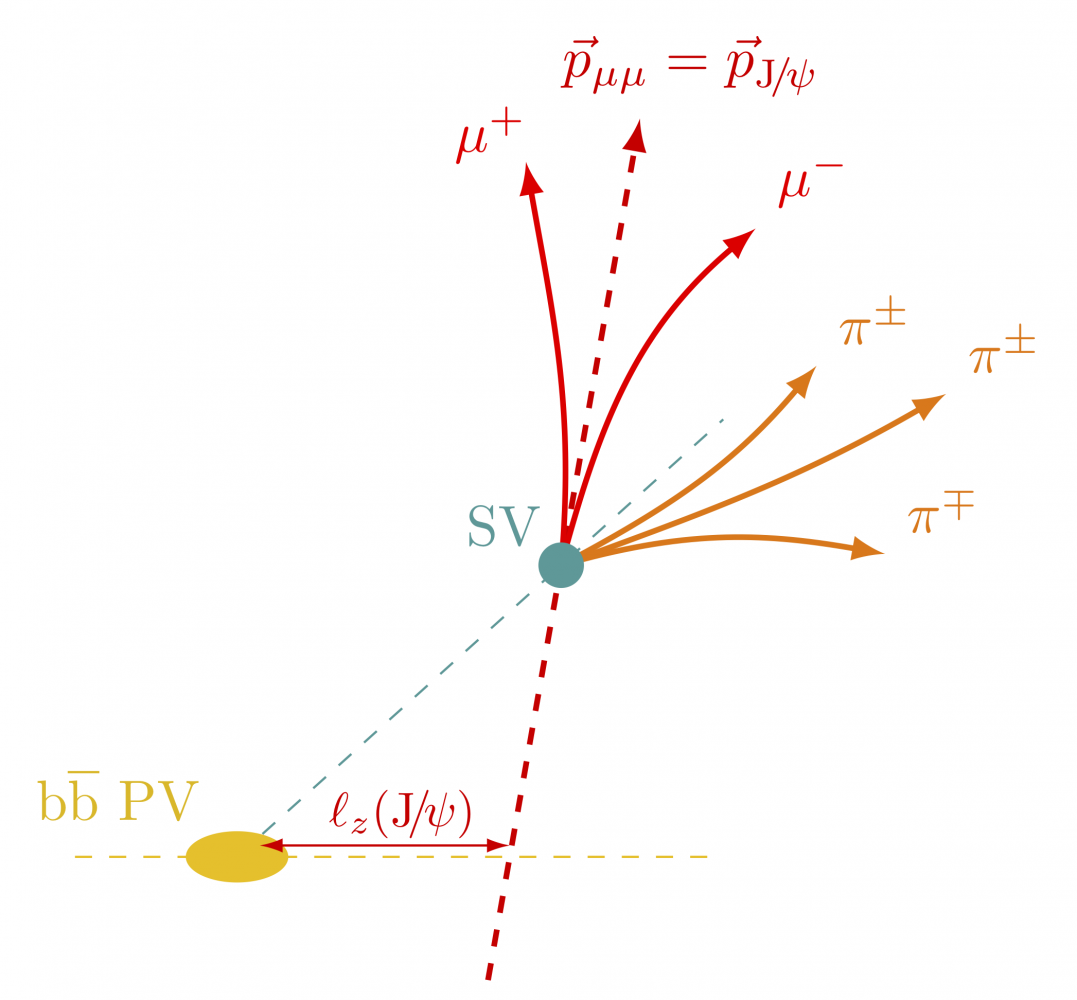
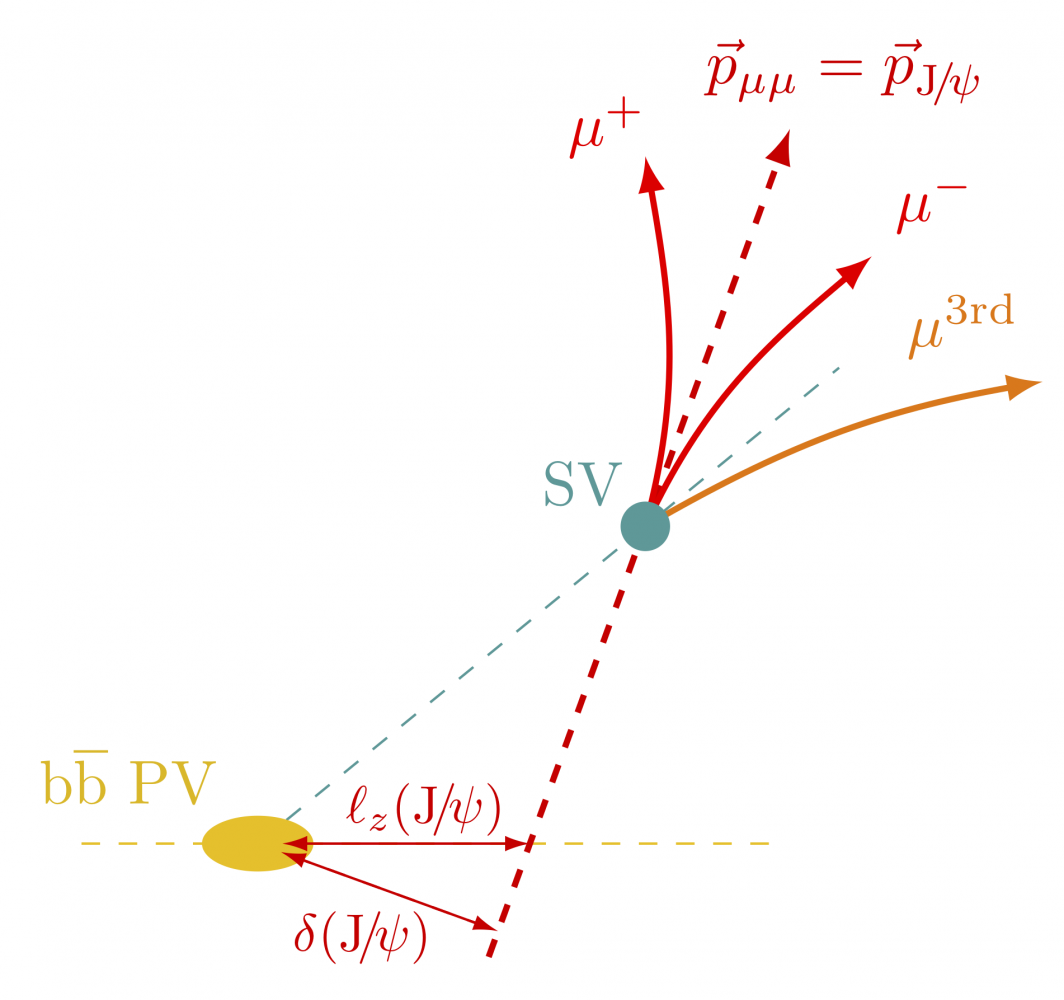
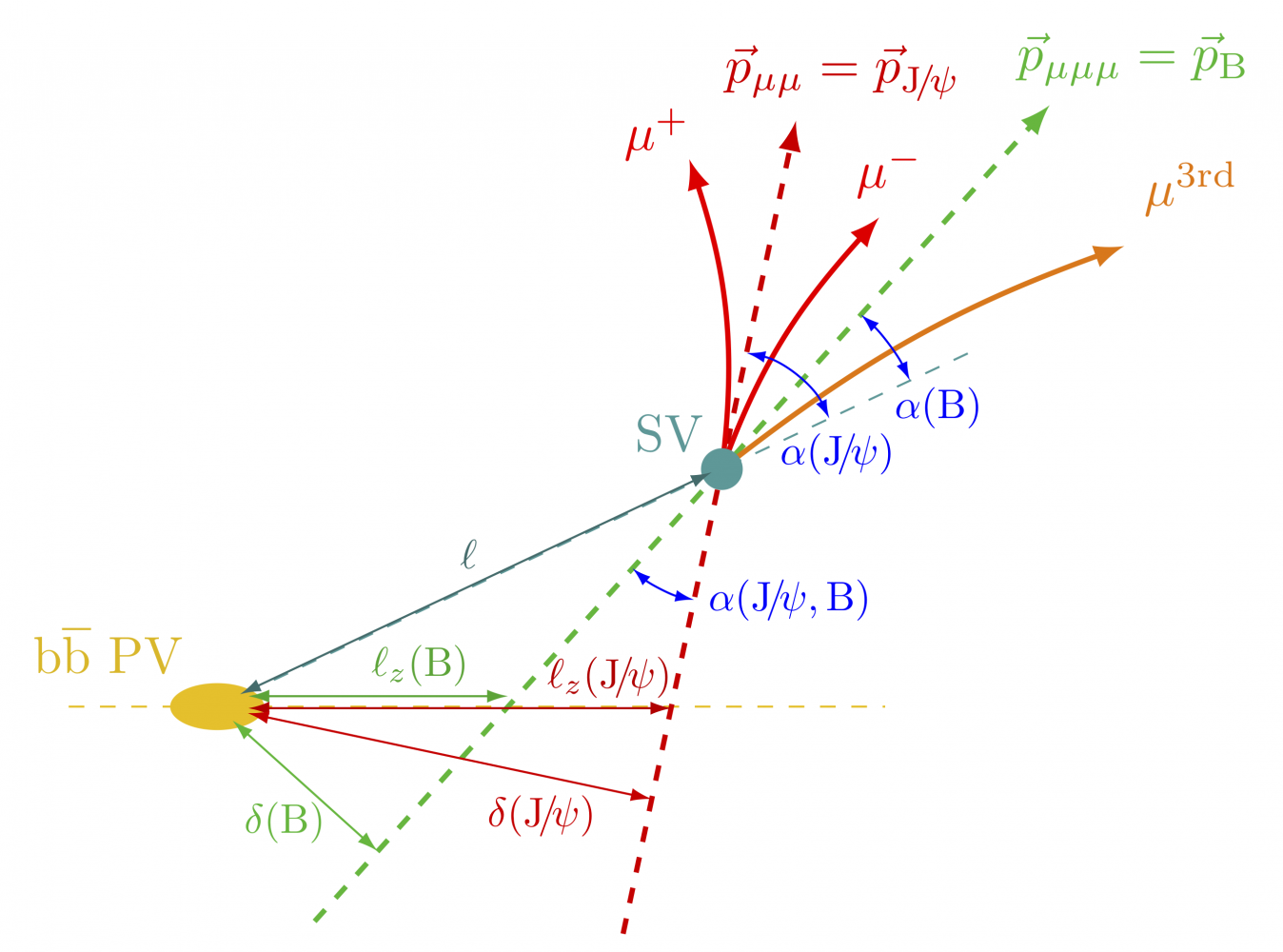
Impact parameters

Examples of defining impact parameters in proton collisions (full code).

Timelines and scales

Examples of a simple time or energy scale with labels and arrows (full code).

Random timeline:

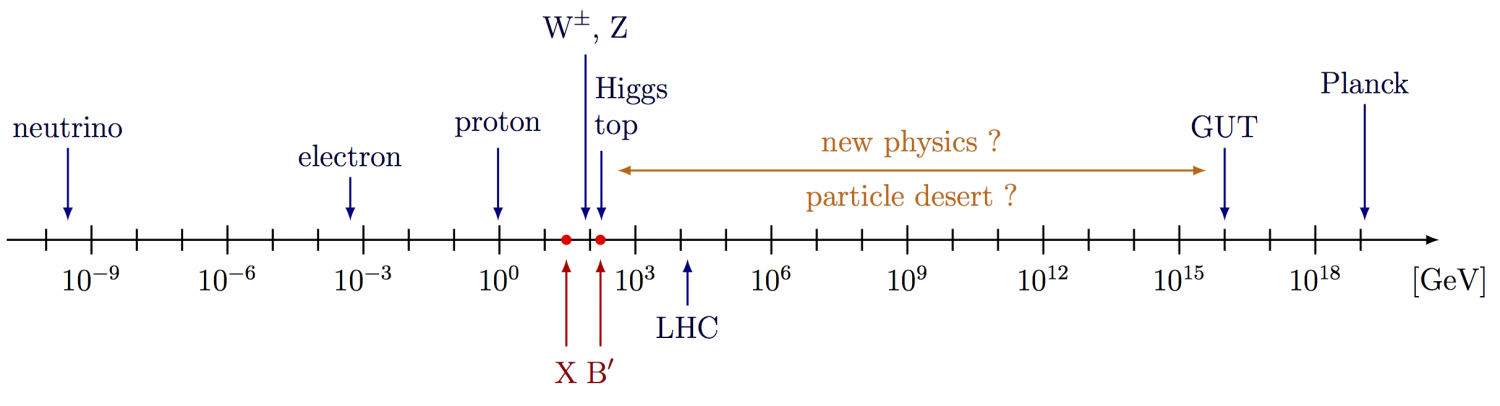
Logarithmic energy scale of particle physics:

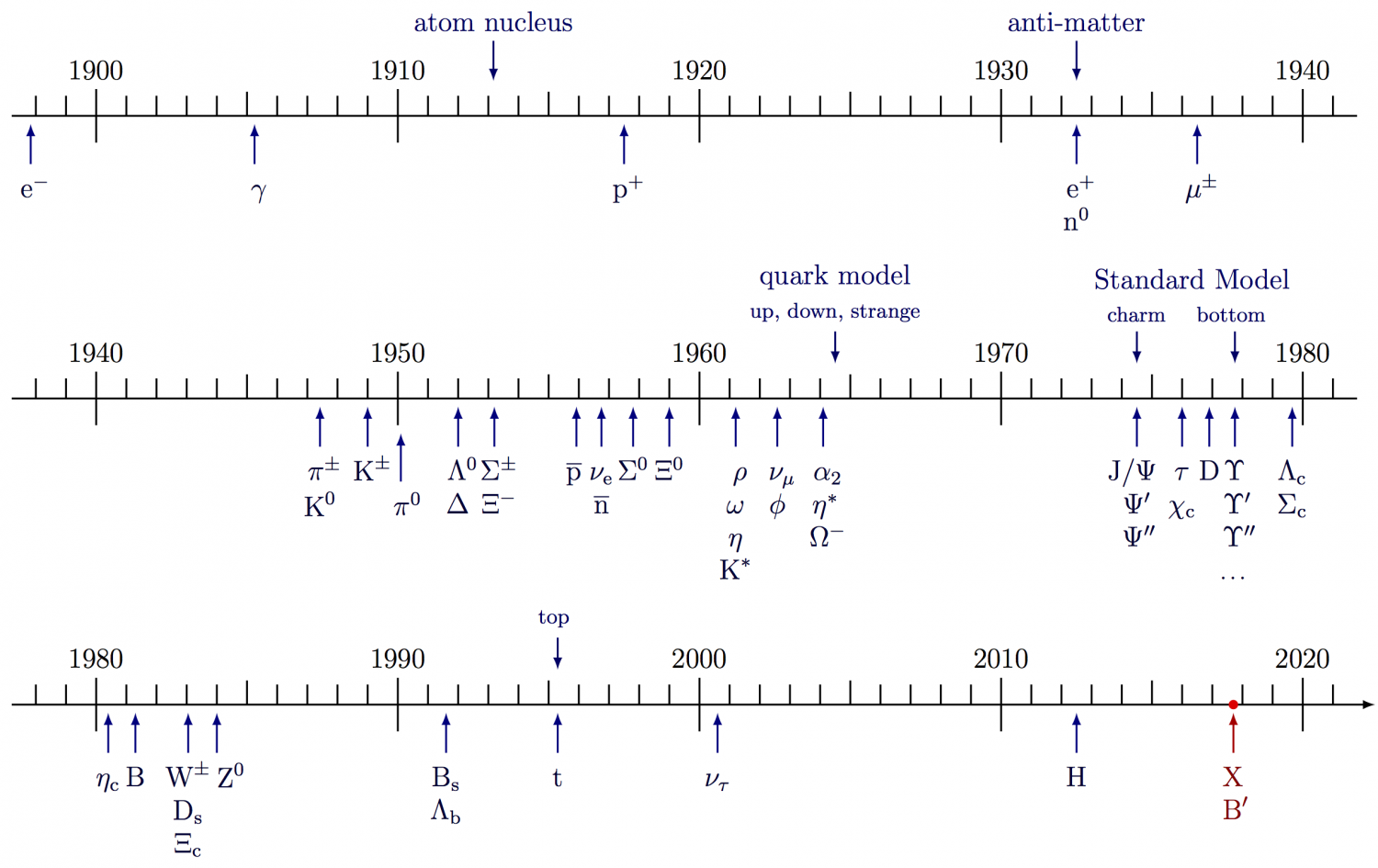
Timeline of particle physics (inspiration):

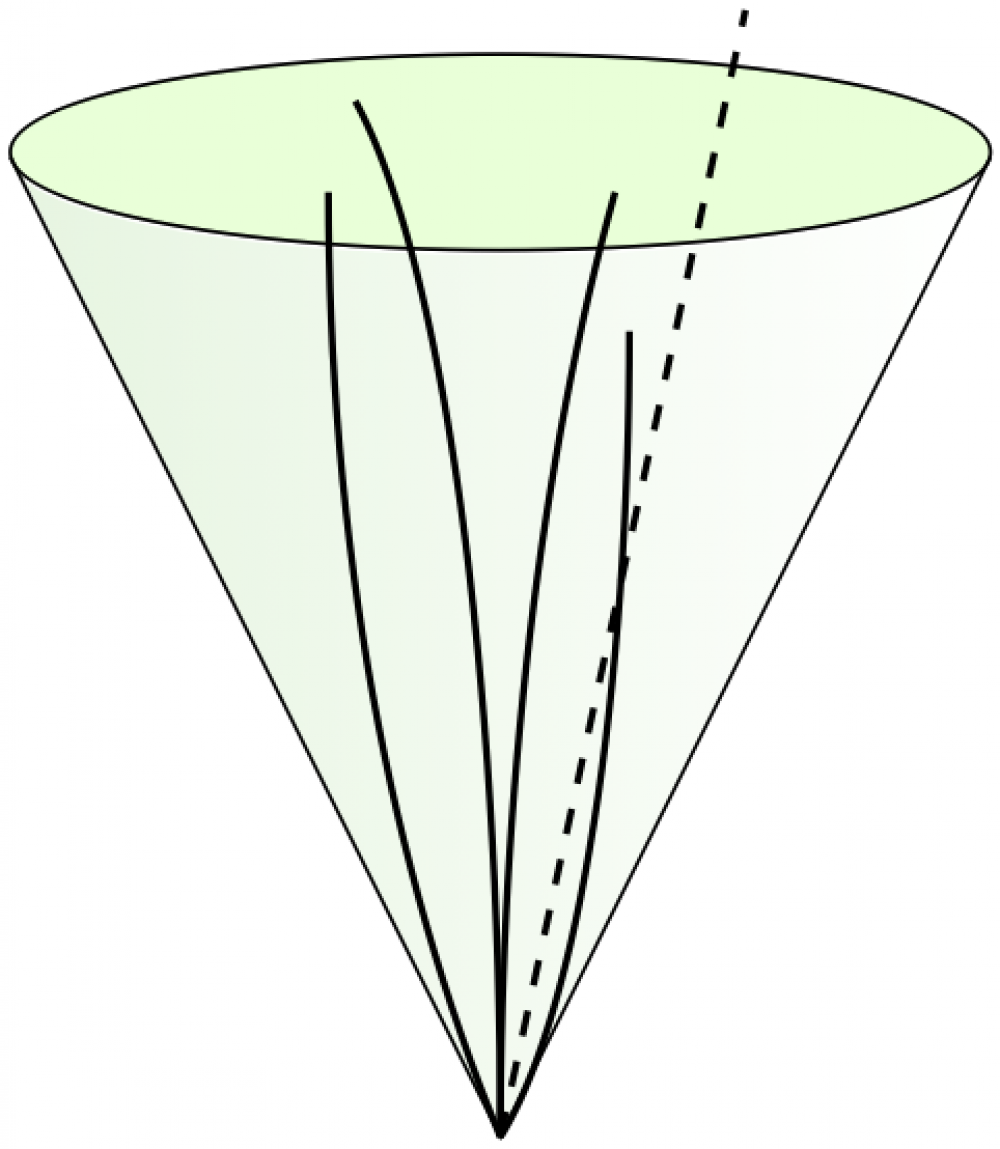
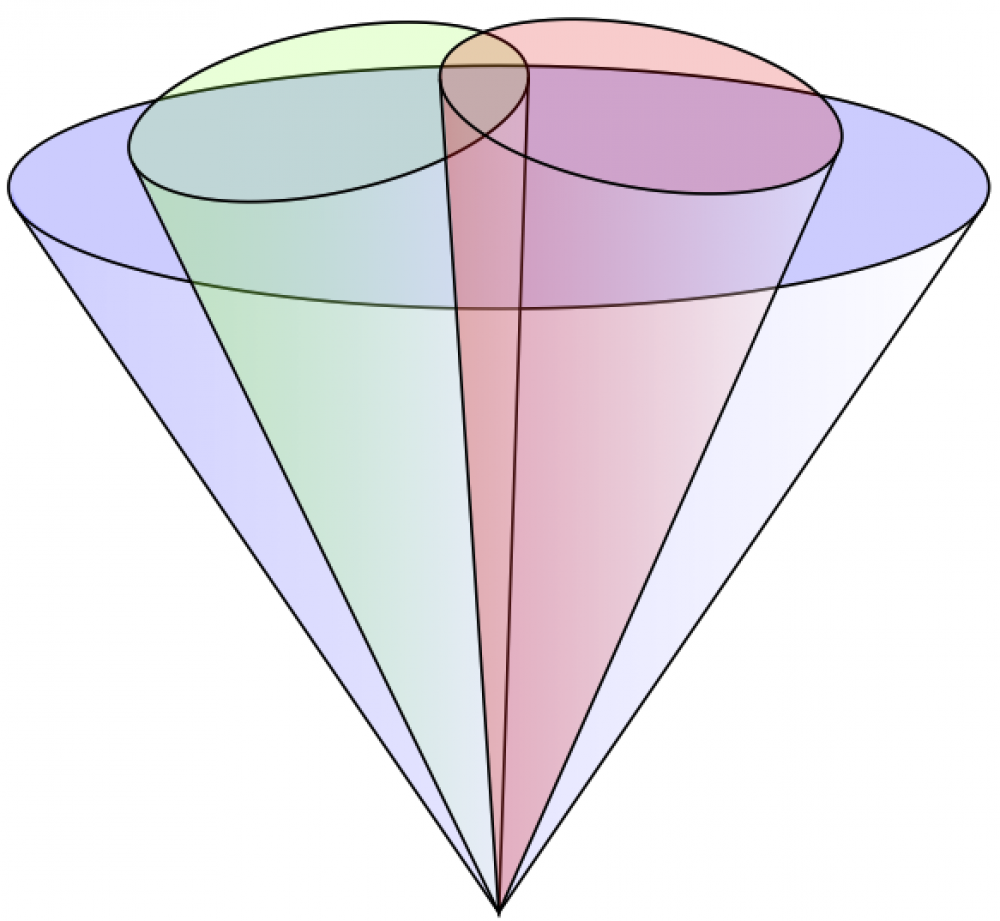
Jets cones

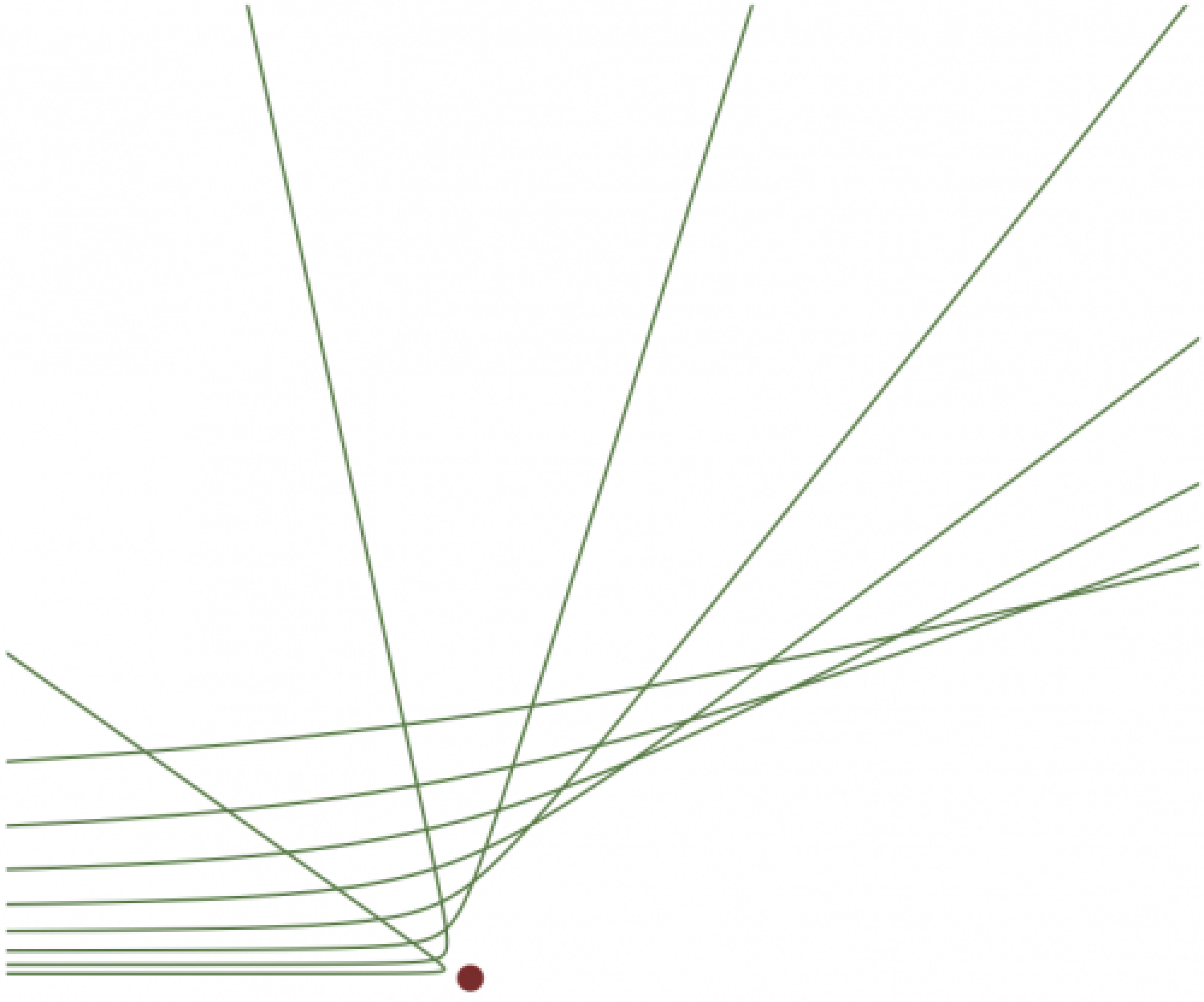
Two examples of cones. Full code can be found here.

\begin{tikzpicture}
 
  % cone variables
  \def\x{2.0}
  \def\y{4.0}
  \def\R{\x}
  \def\yc{\y+0.02}
  \def\e{0.4}
 
  % cone shades + frame
  \shade[right color=white,left color=mylightgreen,opacity=0.3]
    (-\x,\yc) -- (-2,4) arc (180:360:{\R} and \e) -- (\x,\yc) -- (0,0) -- cycle;
  \draw[fill=green,opacity=0.2]
    (0,\yc) circle ({\R} and \e);
  \draw
    (-\x,\y) -- (0,0) -- (\x,\y);
  \draw
    (0,\yc) circle ({\R} and \e);
 
  % tracks
  \draw[thick]
    (0,0) arc (320:360:-3 and 6.0); %node[above] {1};
  \draw[thick]
    (0,0) arc (-70:  0:0.8 and 3.5); %node[above] {2};
  \draw[thick]
    (0,0) arc (  0: 70:0.9 and 4.5); %node[above] {3};
  \draw[thick]
    (0,0) arc (180:140:2 and 6.0); %node[above] {4};
  \draw[thick,dashed]
    (0,0) -- (1,4.6);
 
\end{tikzpicture}

\begin{tikzpicture}
 
  % AK8 variables
  \def\x{2.4}
  \def\y{3.5}
  \def\R{\x+0.02}
  \def\yc{\y+0.08}
  \def\e{0.6}
 
  % AK8 cone
  \shade[right color=white,left color=blue,opacity=0.2]
    (-\x,\y) -- (-\x,\yc) arc (180:360:{\R} and \e) -- (\x,\y) -- (0,0) -- cycle;
  \draw[fill=blue,opacity=0.2]
    (0,\yc) circle ({\R} and \e);
  \draw
    (-\x,\y) -- (0,0) -- (\x,\y);
  \draw
    (0,\yc) circle ({\R} and \e);
 
  % AK4 variables
  \def\x{1.0}
  \def\y{4.0}
  \def\R{\x+0.005}
  \def\yc{\y+0.04}
  \def\e{0.4}
 
  % AK4 cone 1
  \begin{scope}[rotate=12]
    \shade[right color=white,left color=green,opacity=0.3]
      (-\x,\yc) -- (-\x,\yc) arc (180:360:{\R} and \e) -- (\x,\yc) -- (0,0) -- cycle;
    \draw[fill=green,opacity=0.2]
      (0,\yc) circle ({\R} and \e);
    \draw
      (-\x,\y) -- (0,0) -- (\x,\y);
    \draw
      (0,\yc) circle ({\R} and \e);
  \end{scope}
 
  % AK4 cone 2
  \begin{scope}[rotate=-10]
    \shade[right color=white,left color=red,opacity=0.3]
      (-\x,\yc) -- (-\x,\yc) arc (180:360:{\R} and \e) -- (\x,\yc) -- (0,0) -- cycle;
    \draw[fill=red,opacity=0.2]
      (0,\yc) circle ({\R} and \e);
    \draw
      (-\x,\y) -- (0,0) -- (\x,\y);
    \draw
      (0,\yc) circle ({\R} and \e);
  \end{scope}
 
\end{tikzpicture}

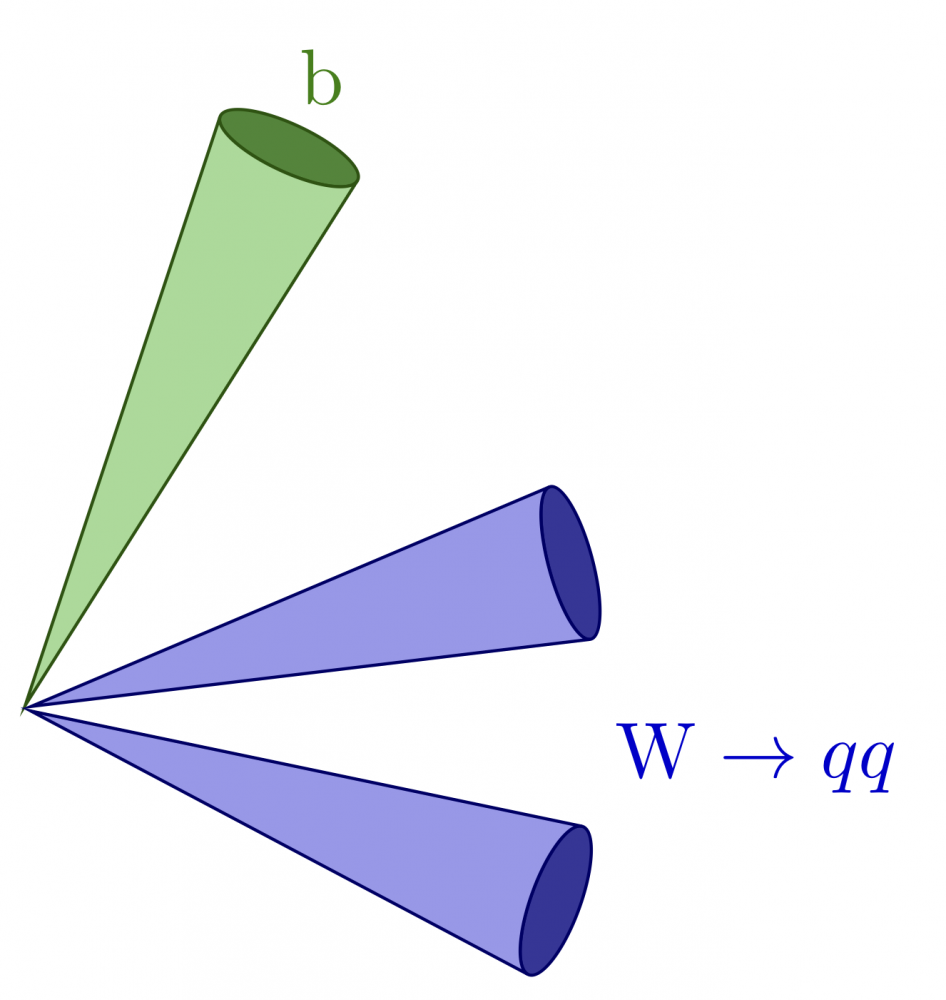
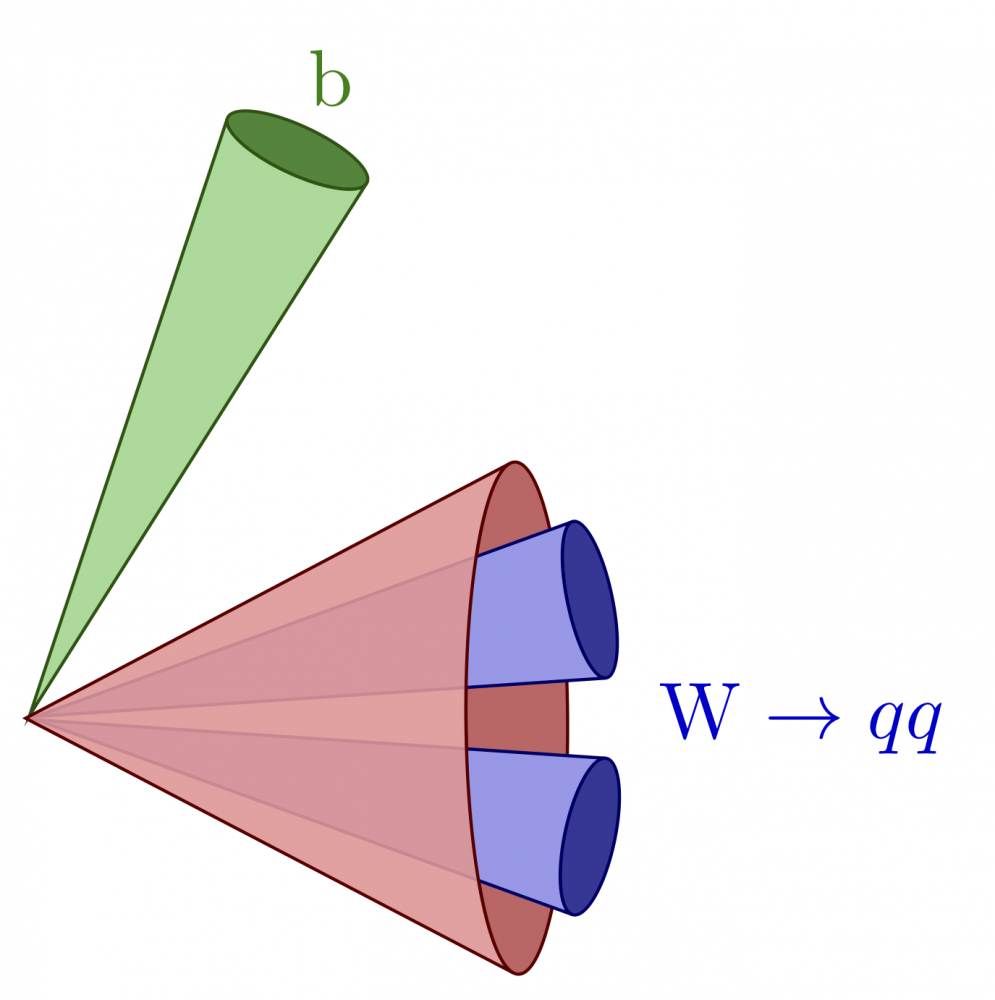
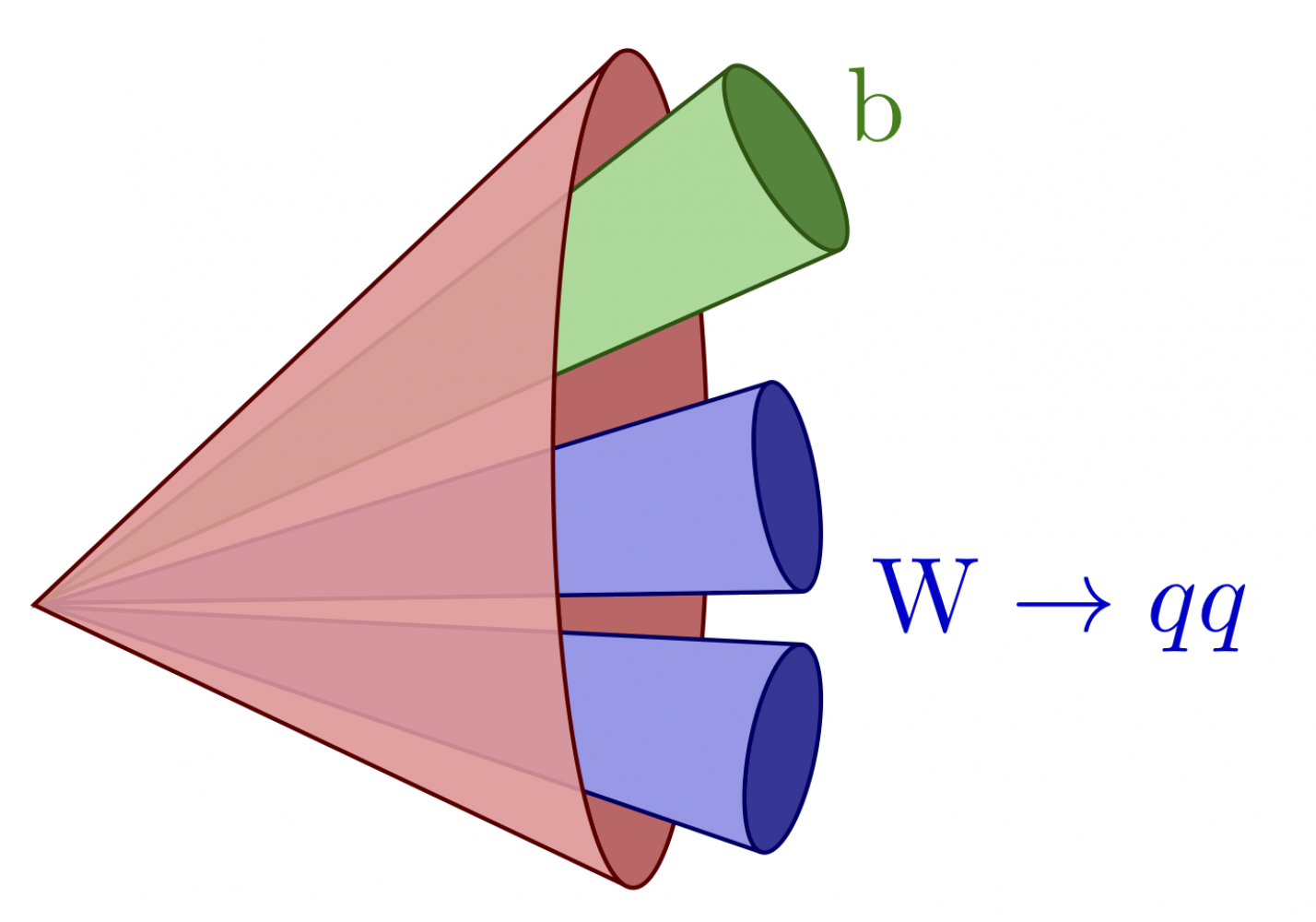
Top jets

The full code can be found here.

\newcommand\jetcone[5][blue]{{
  \pgfmathanglebetweenpoints{\pgfpointanchor{#2}{center}}{\pgfpointanchor{#3}{center}}
  \edef\ang{#4/2}
  \edef\e{#5}
  \edef\vang{\pgfmathresult} % angle of vector OV
  \tikzmath{
    coordinate \C;
    \C = (#2)-(#3);
    \x = veclen(\Cx,\Cy)*\e*sin(\ang)^2; % x coordinate P
    \y = tan(\ang)*(veclen(\Cx,\Cy)-\x); % y coordinate P
    \a = veclen(\Cx,\Cy)*sqrt(\e)*sin(\ang); % vertical radius
    \b = veclen(\Cx,\Cy)*tan(\ang)*sqrt(1-\e*sin(\ang)^2); % horizontal radius
    \angb = acos(sqrt(\e)*sin(\ang)); % angle of P in ellipse
  }
  \coordinate (tmpL) at ($(#3)-(\vang:\x pt)+(\vang+90:\y pt)$); % tangency
  \draw[thin,#1!40!black,fill=#1!50!black!80,rotate=\vang]
    (#3) ellipse({\a pt} and {\b pt});
  \draw[thin,#1!40!black,fill=#1!80!black!40,rotate=\vang]
    (tmpL) arc(180-\angb:180+\angb:{\a pt} and {\b pt})
    -- ($(#2)+(\vang:0.018)$) -- cycle;
}}
 
\begin{tikzpicture}
  \def\R{2.5}
  \coordinate (O) at (0,0);
  \coordinate (BJ) at ( 65:1.1*\R); % b jet 1
  \coordinate (J1) at ( 15:1.0*\R); % q jet 1
  \coordinate (J2) at (-20:1.0*\R); % q jet 2
  \jetcone[green!80!black]{O}{BJ}{14}{0.10}
  \jetcone{O}{J1}{16}{0.08}
  \jetcone{O}{J2}{16}{0.10}
  \node[green!50!black] at (65:1.24*\R) {b};
  \node[blue!80!black,right] at (-5:1.00*\R) {$\mathrm{W} \to qq$};
\end{tikzpicture}

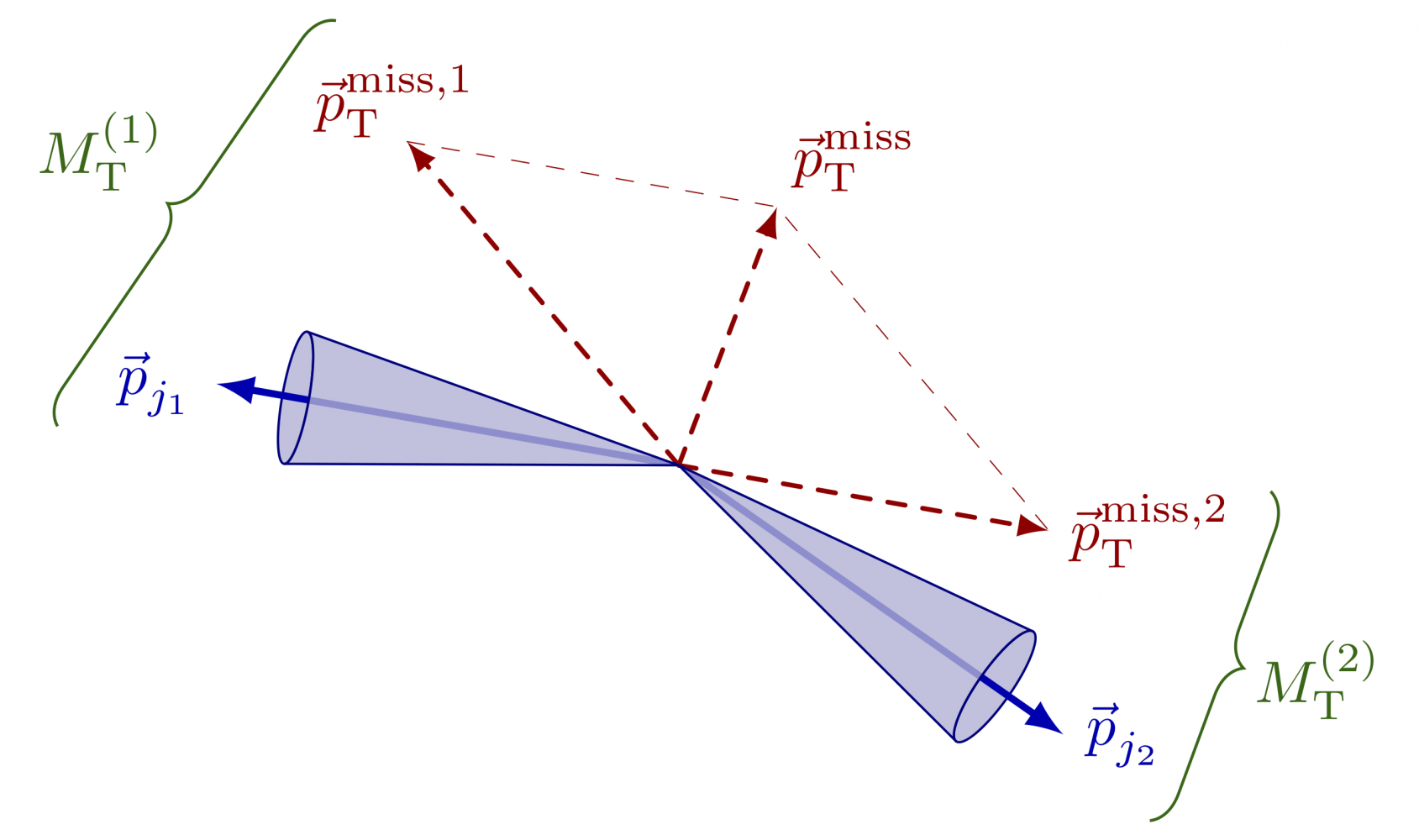
Jet vectors

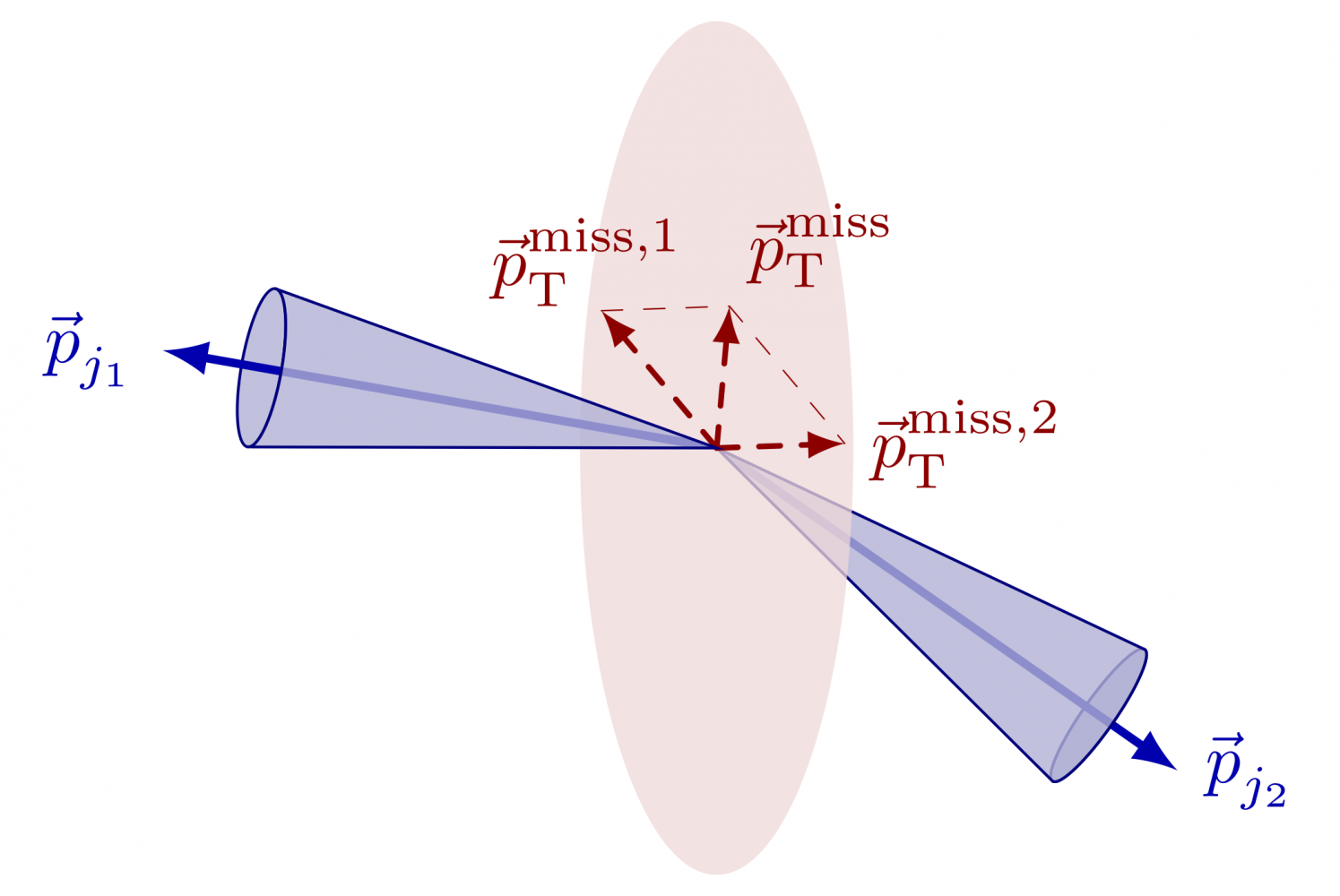
One can do some projections of jet and MET vectors to construct variables like MT2 in SUSY searches. The full code can be found here.

\newcommand\jetcone[4]{
  \pgfmathanglebetweenpoints{\pgfpointanchor{#1}{center}}{\pgfpointanchor{#2}{center}}
  \edef\tmpang{\pgfmathresult}
  \coordinate (tmpC) at ($(#2)+(\tmpang-180:{abs(#4)+0.4})$); % center
  \coordinate (tmpL) at ($(tmpC)+(\tmpang+90:#3)$); % left corner
  \coordinate (tmpR) at ($(tmpC)+(\tmpang-90:#3)$); % right corner
  \draw[cone,rotate=\tmpang]
    %(tmpR) arc(90:-90:{#4} and {#3});
    (tmpC) ellipse({#4} and {#3});
  \begin{scope}
    \clip[rotate=\tmpang] (tmpR) -- (#1) -- (tmpL) arc(90:-90:{#4+0.6} and {#3});
    \draw[vector] (#1) -- (#2);
  \end{scope}
  \draw[cone,rotate=\tmpang]
    (tmpL) arc(90:270:{#4} and {#3}) -- (#1) -- cycle;
}
 
% MT2
\begin{tikzpicture}
  \def\R{2.8}
  \coordinate (O) at (0,0);
  \coordinate (J1) at (170:\R); % jet 1 pT
  \coordinate (J2) at (-35:\R); % jet 2 pT
  \coordinate (M1) at (130:0.9*\R); % pTmiss component 1
  \coordinate (M2) at (-10:0.8*\R); % pTmiss component 2
  \coordinate (M) at ($(M1)+(M2)$); % total missing momentum
 
  % PTMISS
  \draw[ptmiss,-,very thin] (M1) -- (M) -- (M2);
  \draw[ptmiss] (O) -- (M1) node[left=2,above=-3] {$\ptmissX{1}$};
  \draw[ptmiss] (O) -- (M2) node[right=0] {$\ptmissX{2}$};
  \draw[ptmiss] (O) -- (M) node[above right=-1] {$\ptmiss$};
 
  % JET CONES
  %\draw[vector] (O) -- (J1);
  %\draw[vector] (O) -- (J2);
  %\cone{O}{J1}{0.3}{0.15}
  \jetcone{O}{J1}{0.4}{0.08}
  \jetcone{O}{J2}{0.4}{0.10}
  \node[vector,left] at (J1) {$\vv{p}_{j_1}$};
  \node[vector,right] at (J2) {$\vv{p}_{j_2}$};
 
  % CURLY BRACE
  \draw[line width=0.5,mygreen,decorate,decoration={brace,amplitude=6}]
    ($(J1)+(195:0.35*\R)$) -- ($(M1)+(120:0.30*\R)$) node[midway,above left=2] {$\MTX{1}$};
  \draw[line width=0.5,mygreen,decorate,decoration={brace,amplitude=6}]
    ($(M2)+(10:0.48*\R)$) -- ($(J2)+(-45:0.26*\R)$) node[midway,below=4,right=4] {$\MTX{2}$};
 
\end{tikzpicture}

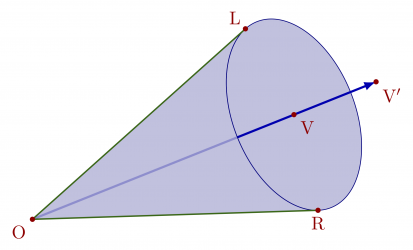
Tangent to a circle or ellipse

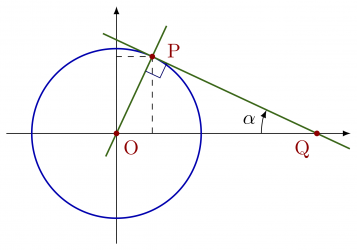
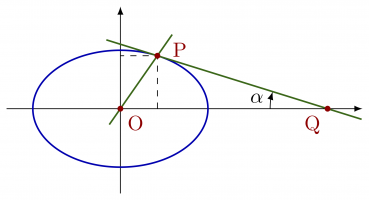
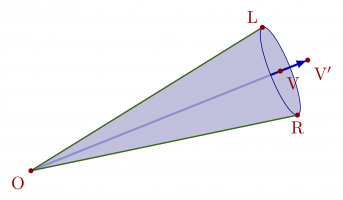
Some different methods of finding the tangent to a circle or ellipse in TikZ. Using these methods a nice cone can be made. The full code can be found here.

% TANGENT to CIRCLE - known: r, q
\begin{tikzpicture}
  \def\r{1.5} % radius
  \def\q{4} % distance center-external point q = |OQ|
  \def\x{{\r^2/\q}} % Q x coordinate
  \def\y{{\r*sqrt(1-(\r/\q)^2}} % Q y coordinate
  \coordinate (O) at (0,0); % circle center O
  \coordinate (Q) at (\q,0); % external point Q
  \coordinate (P) at (\x,\y); % point of tangency, P
  \draw[->] (0,-1.3*\r) -- (0,1.5*\r);
  \draw[->] (-1.3*\r,0) -- (\q+0.4*\r,0);
  \draw[dashed] (\x,0) |- (0,\y);
  \draw[myblue,thick] (O) circle(\r);
  \draw[mygreen,thick] ($(Q)!-0.2!(P)$) -- ($(Q)!1.3!(P)$);
  \draw[mygreen,thick] ($(O)!-0.3!(P)$) -- ($(O)!1.4!(P)$);
  \rightAngle{Q}{P}{O}{0.40}
  \fill[myred] (O) circle(0.05) node[below right] {O};
  \fill[myred] (Q) circle(0.05) node[below left] {Q};
  \fill[myred] (P) circle(0.05) node[above=3,right=4] {P};
\end{tikzpicture}
 
% TANGENT to ELLIPSE - known: a, b, q
\begin{tikzpicture}
  \def\a{1.5} % horizontal radius
  \def\b{1.0} % vertical radius
  \def\q{4} % distance center-external point q = |OQ|
  \def\x{{\a^2/\q}} % x coordinate P
  \def\y{{\b*sqrt(1-(\a/\q)^2}} % y coordinate P
  \coordinate (O) at (0,0); % circle center O
  \coordinate (Q) at (\q,0); % external point Q
  \coordinate (P) at (\x,\y); % point of tangency, P
  \draw[->] (0,-\b-0.3*\a) -- (0,\b+0.4*\a);
  \draw[->] (-1.3*\a,0) -- (\q+0.4*\a,0);
  \draw[dashed] (\x,0) |- (0,\y);
  \draw[myblue,thick] (O) ellipse({\a} and {\b});
  \draw[mygreen,thick] ($(Q)!-0.2!(P)$) -- ($(Q)!1.3!(P)$);
  \draw[mygreen,thick] ($(O)!-0.3!(P)$) -- ($(O)!1.4!(P)$);
  \fill[myred] (O) circle(0.05) node[below right] {O};
  \fill[myred] (Q) circle(0.05) node[below left] {Q};
  \fill[myred] (P) circle(0.05) node[above=3,right=4] {P};
\end{tikzpicture}

Table of Contents