Extrapolation and reducing the ndof
Finished my studies on reducing the number of fit parameters. Found the best function as 2 gaussians + landau.
3 gaussians + landau
Expression: 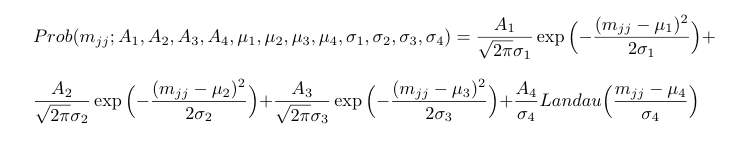
300 GeV
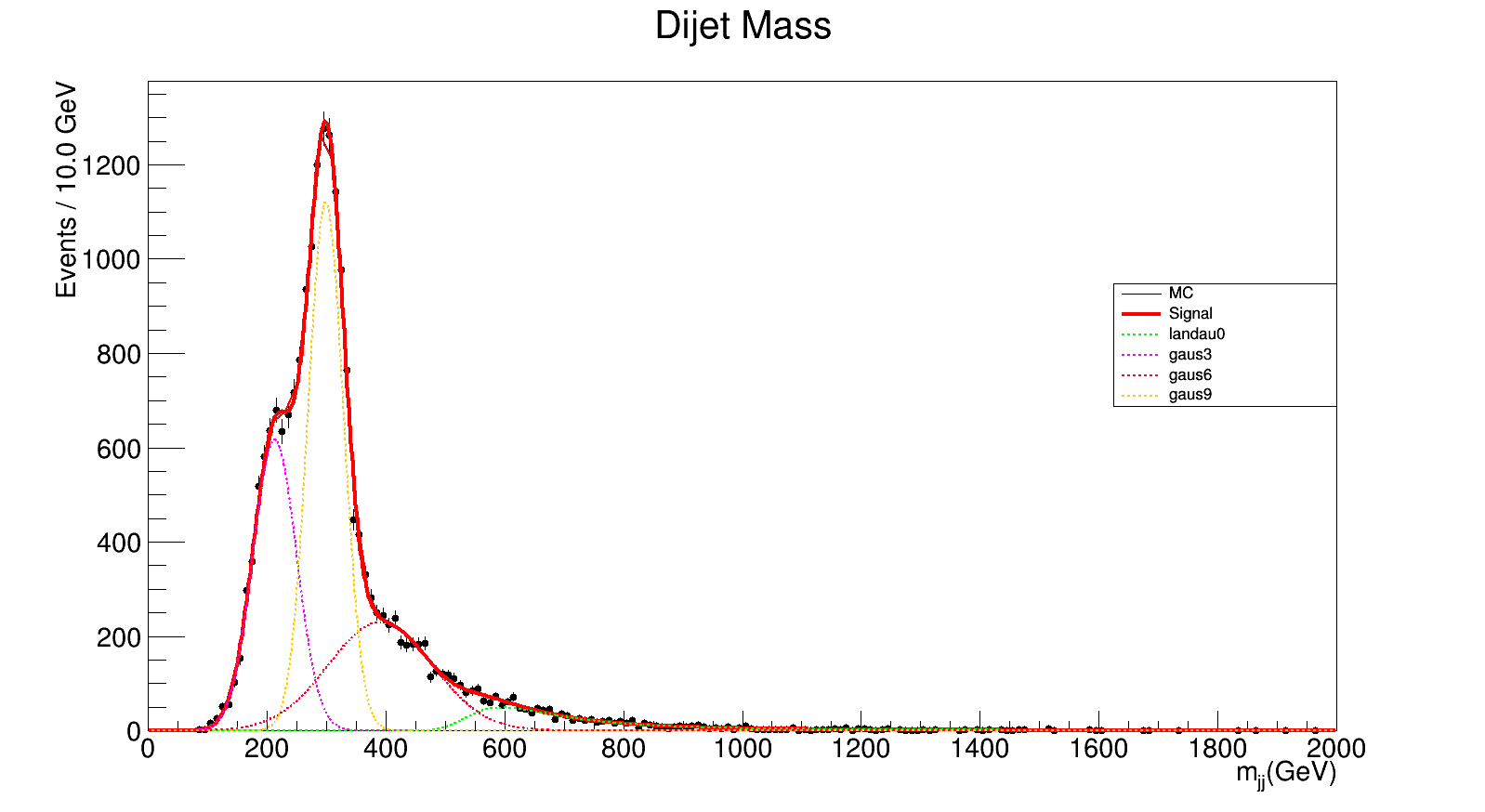
chi_square = 202.423391874/188.0 = 1.07672016954
400 GeV
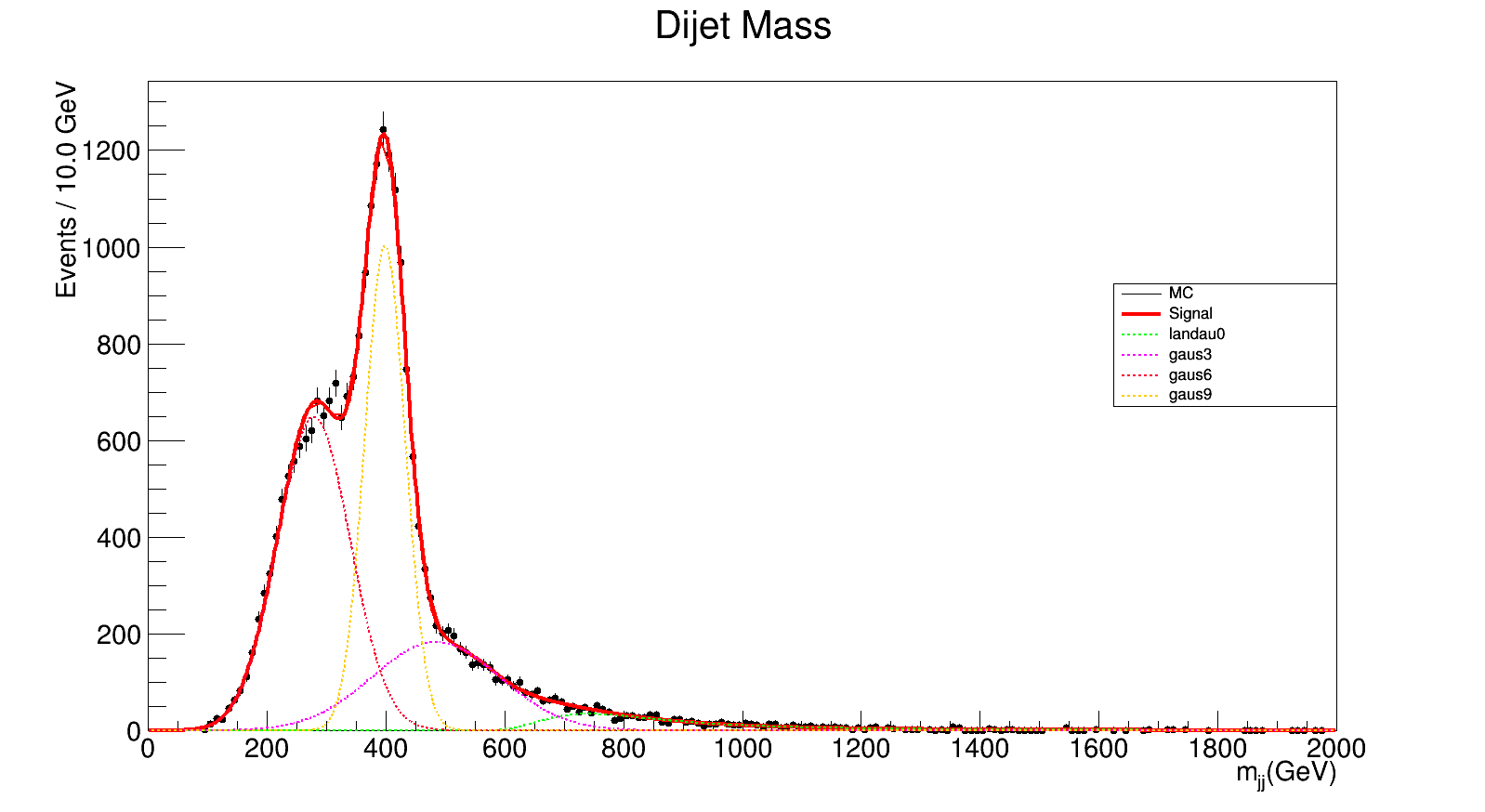
chi_square = 254.599910266/188.0 = 1.35425484184
500 GeV
(Actually, I forced all functions to have non-zero area. You can see that the third gaussian (orange) has very small sigma and non-zero area and describes only 2 points, that has no sense. However, if I free the lower bound of the normalisation constant (area) to zero, third gaussian disappear. So, the 4th function is redundant. This was one of the reason why I started to find the way to fit the signal with at most 3 functions.)

chi_square = 455.035302783/188.0 = 2.42040054672
600 GeV
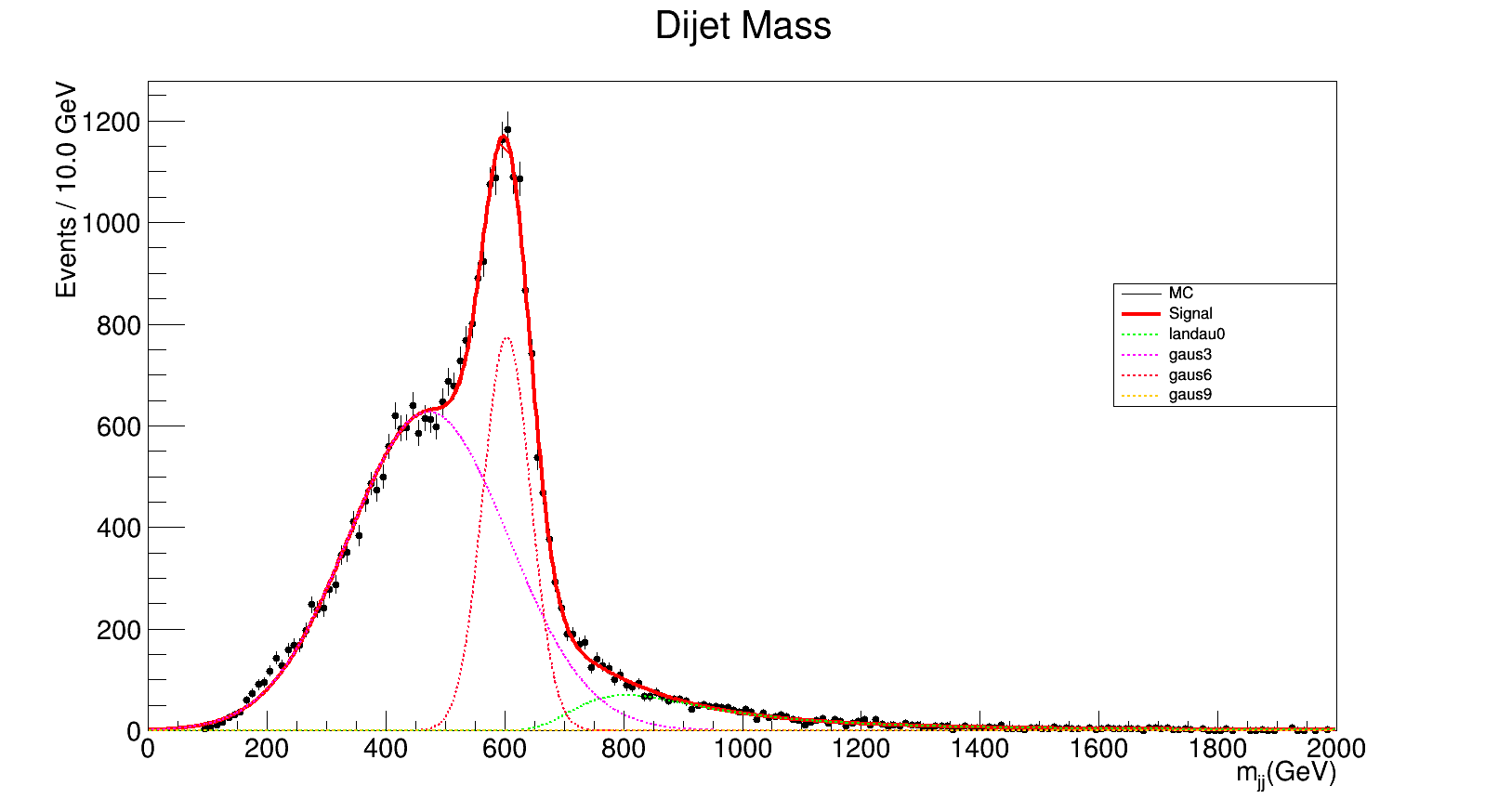
chi_square = 606.474750337/188.0 = 3.22592952307
2 gausians + landau
Expression: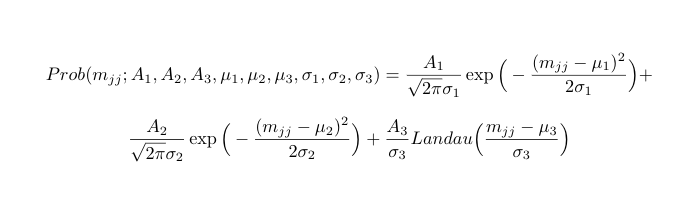
300 GeV
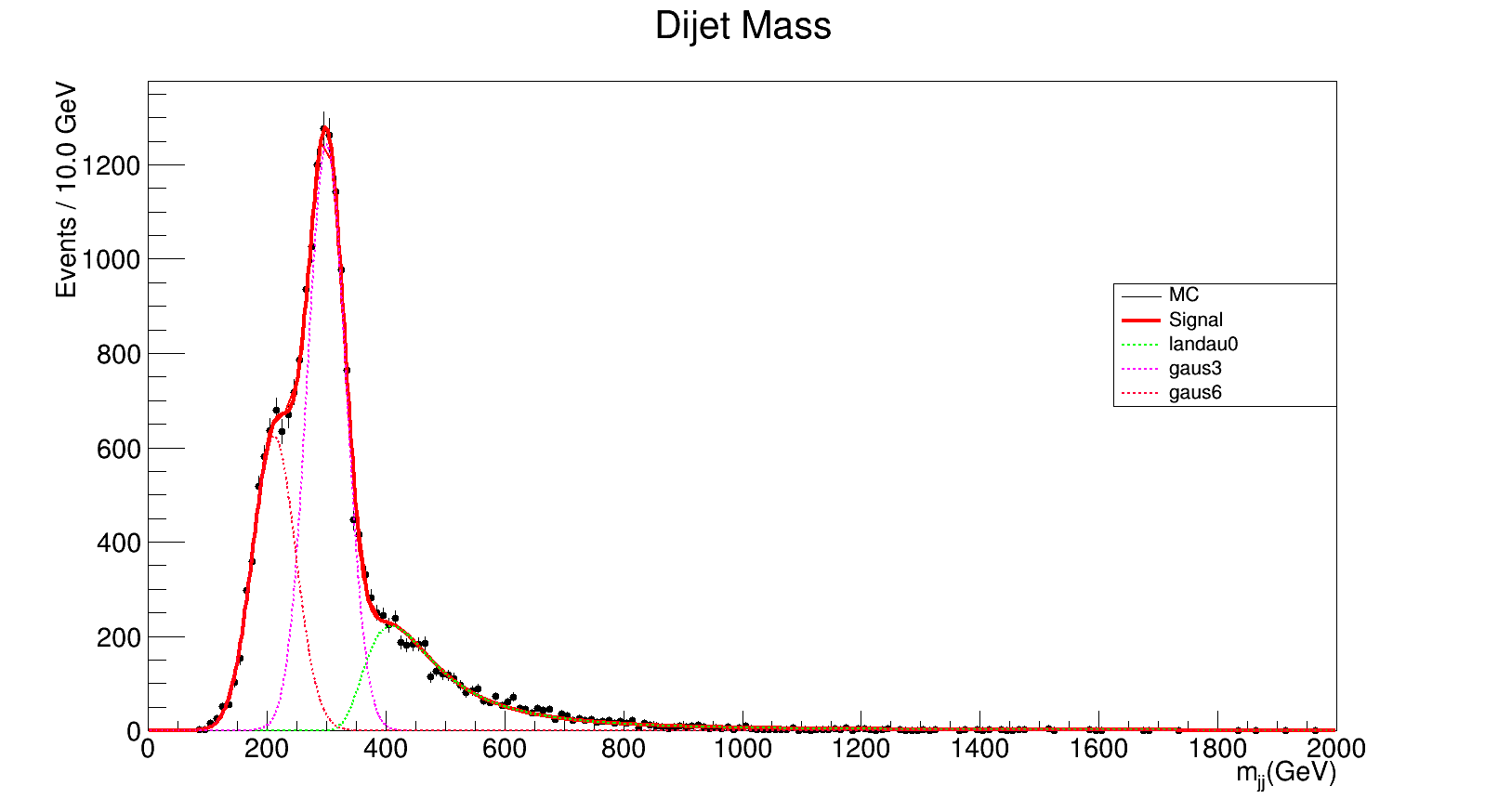
chi_square = 342.1863381/191.0 = 1.79155150838
400 GeV
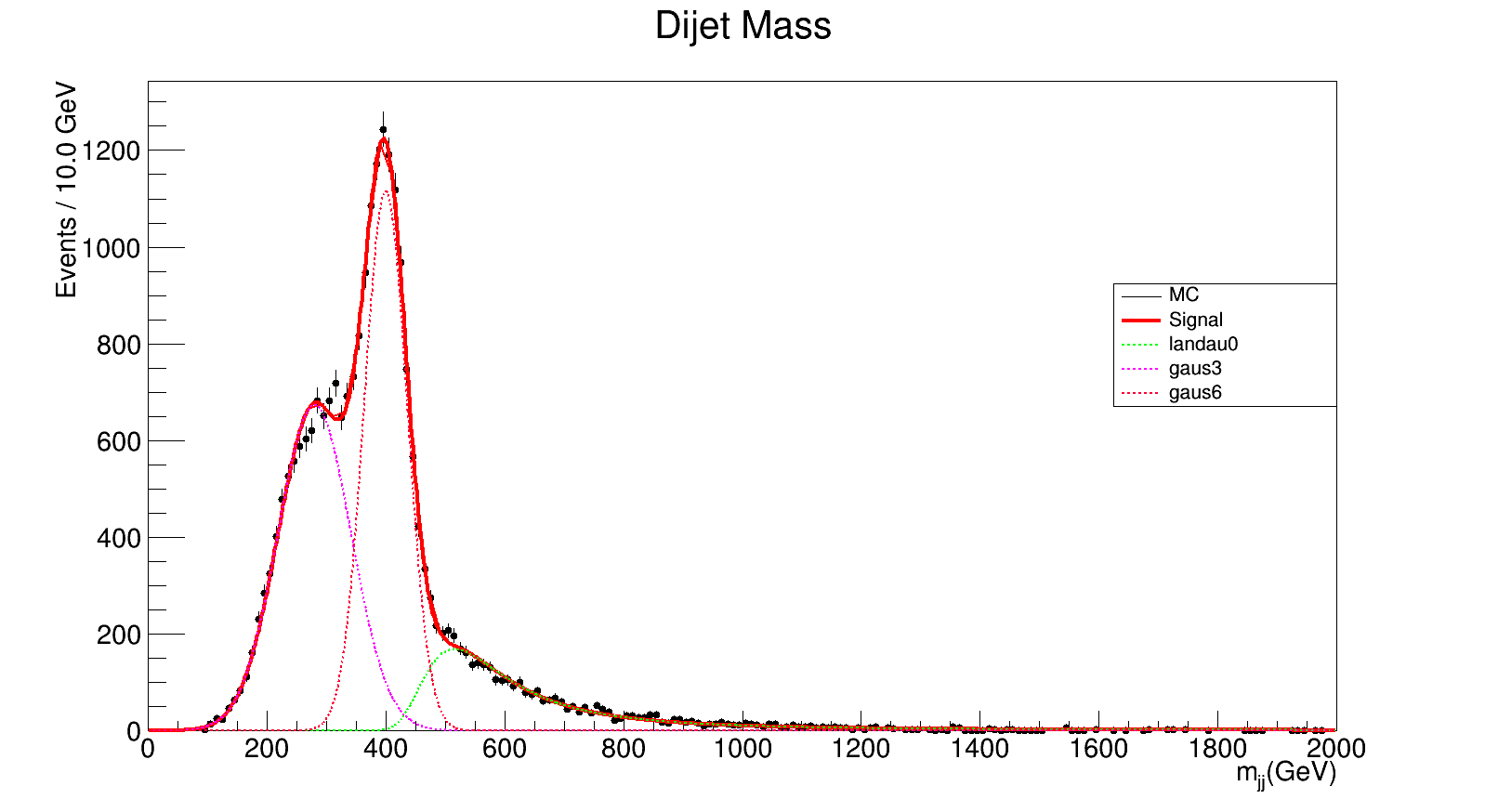
chi_square = 349.860731707/191.0 = 1.83173157962
500 GeV
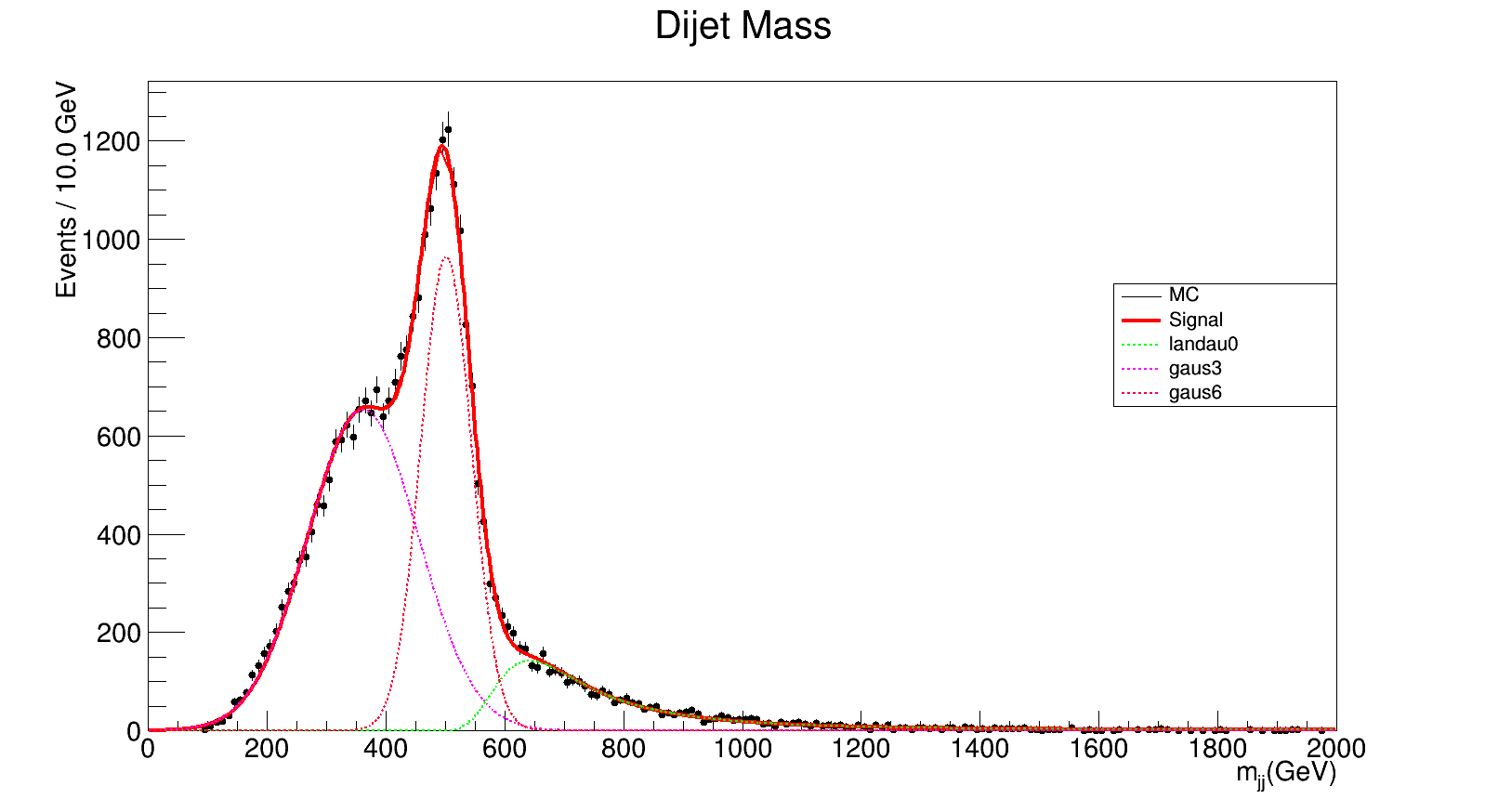
chi_square = 457.792421761/191.0 = 2.3968189621
600 GeV
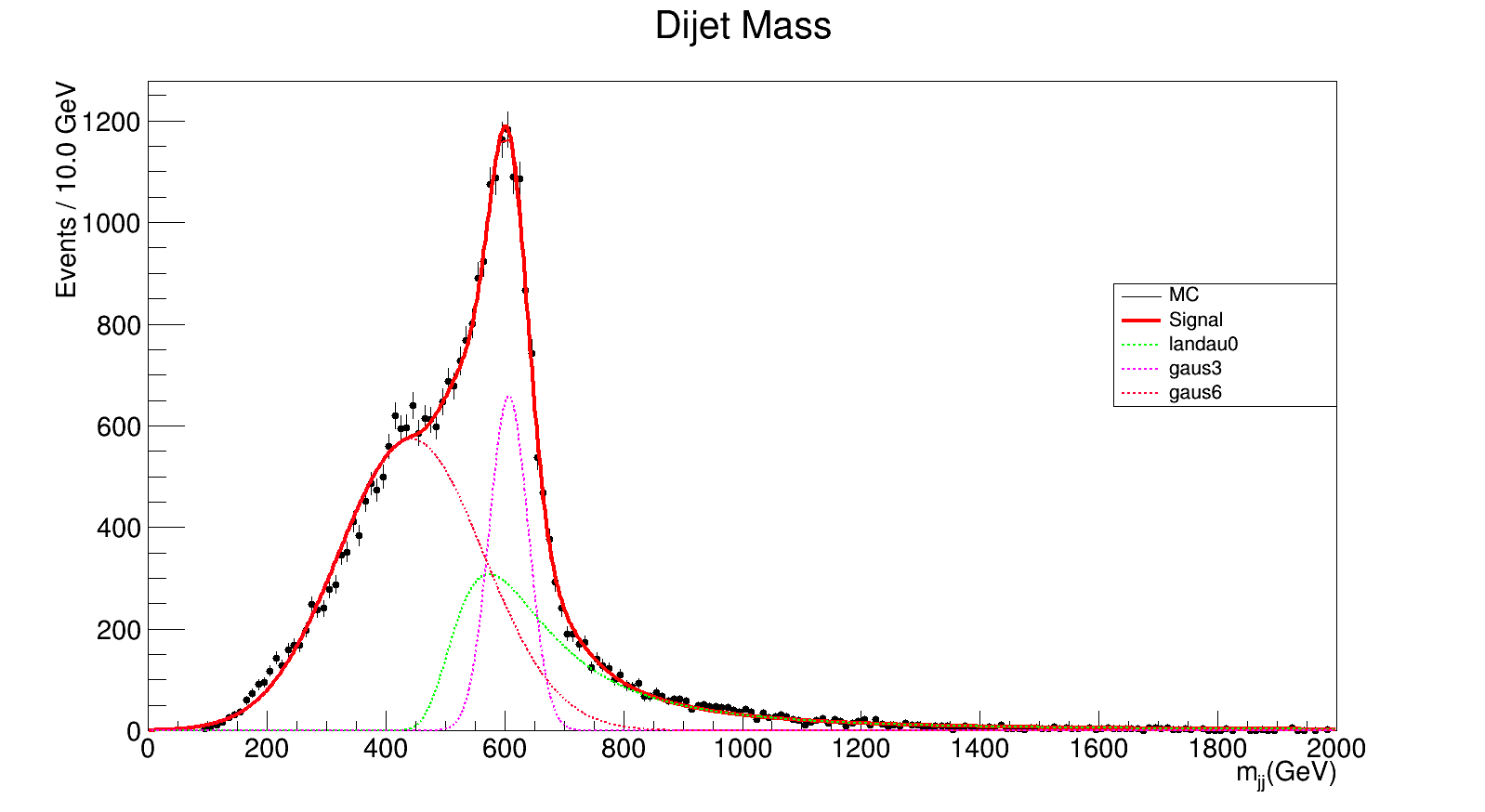
chi_square = 657.261829338/191.0 = 3.44116141014
The difference in the chi square lies within 1. So 4 function doesn't improve the fit too much wrt the 3 functions.
Extrapolation
Using the extrapolation formula 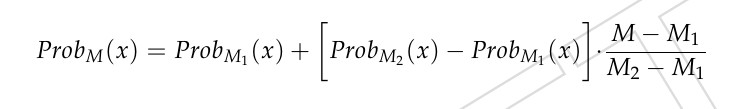 I obtained the following results.
I obtained the following results.
Mass of the 1st resonance is 300 GeV, mass of the 2nd is 500 GeV
Extrapolation for 300 GeV (should be the same as fit). On X axis mjj/Mres, where Mres is the mass of the resonance (300 GeV). On Y axis - Events / 10 Gev.
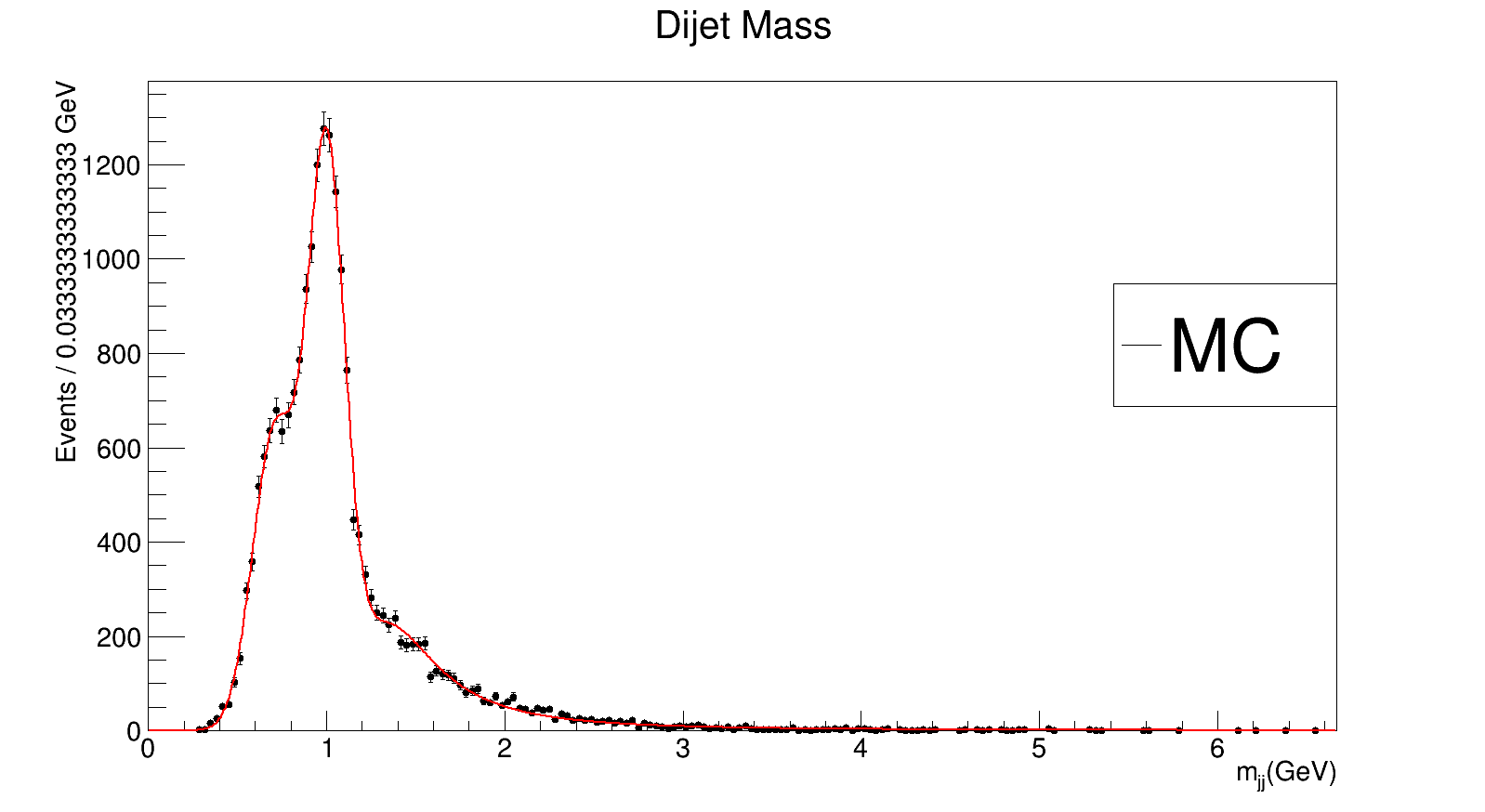 Extrapolation for 400 GeV. On X axis
Extrapolation for 400 GeV. On X axis mjj/Mres, where Mres is the mass of the resonance (400 GeV). On Y axis - Events / 10 Gev. Looks not so bad as I expected.
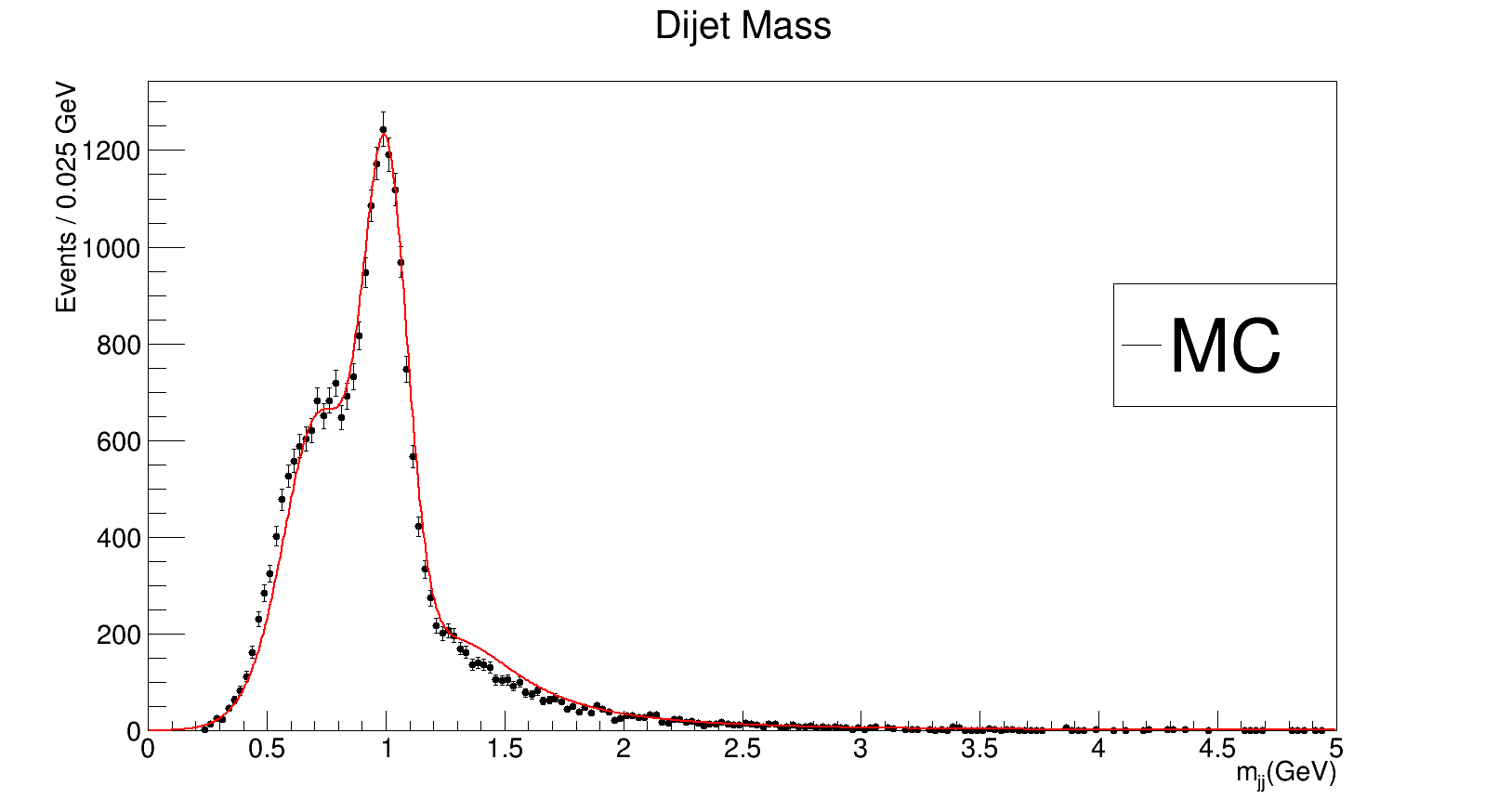 Extrapolation for 500 GeV (should be the same as fit). On X axis
Extrapolation for 500 GeV (should be the same as fit). On X axis mjj/Mres, where Mres is the mass of the resonance (500 GeV). On Y axis - Events / 10 Gev.
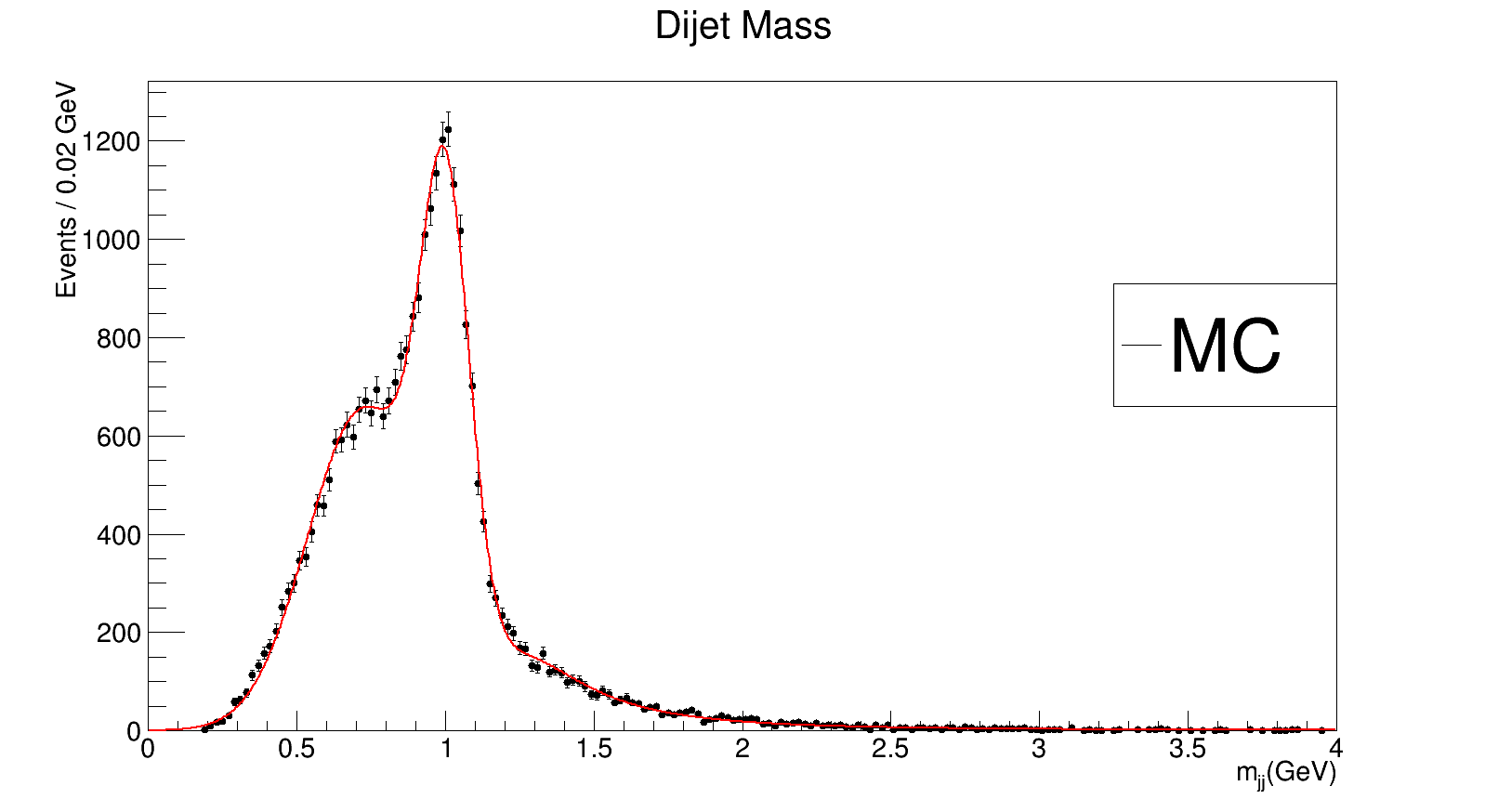
Mass of the 1st resonance is 400 GeV, mass of the 2nd is 600 GeV
Extrapolation for 500 GeV using fit functions for 400 and 600 GeV: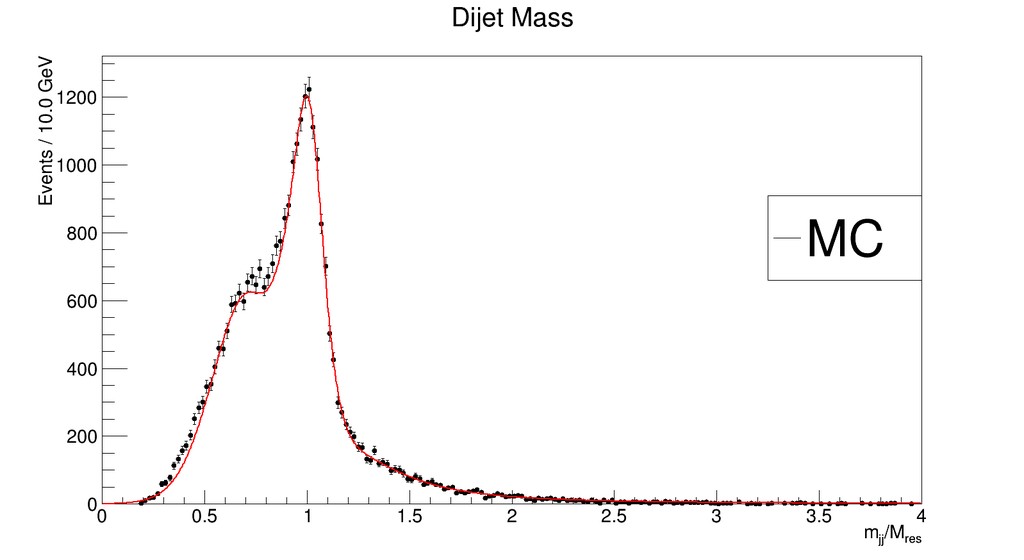
Next steps
- Automise the code to produce the extrapolation function for mass from 400 to 600 GeV with step of 10 GeV.
- Have a look to the README Javier sent us about how to perform the fit

